5. Элементы теории множеств

Множеством называется любое объединение определённых, вполне различимых объектов; их может и не быть вообще. Можно говорить о множестве точек на отрезке [0,1], множестве студентов в группе, множестве снежных дней в июле на экваторе, т.е. множество образуют любые объекты, объединённые по любому признаку. Объекты, составляющие множество, называются элементами множества. Множество, не имеющее ни одного элемента, называется пустым, обозначается Ø. Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным.

Задать множество можно перечислением его элементов. Например, множество, образованное из nэлементова₁, а₂, ..., а_n, обозначаетсяА = {а₁, а₂, ..., а_n}; пишетсяа А(говорится «элемент а при надлежит множеству А»), если а является элементом множестваА, в противном случаеa A.Задать множество можно также, указав общее свойство для всех его и только его элементов. Например, множество равноудалённых от концов отрезка точек. Два множества считаются равными, если состоят из одних и тех же элементов; записываетсяА = В. МножествоBназывается подмножествомА(записываетсяBА), если все элементы множестваА₁являются элементамиА.

Для множеств определены следующие операции: объединение, пересечение, дополнение. ОбъединениеммножествАиВ(записываетсяAB) называется множество, состоящее из элементов как одного, так и второго множества. Например,АиВ– множества точек, принадлежащих некоторым двум кругам, имеющим общие точки, тогда объединениемABбудет фигура, состоящая из общих точек.ПересечениеммножествАиВ(записываетсяАВ) называется множество, состоящее из элементов, принадлежащих как одному, так и второму множеству одновременно.ДополнениеммножестваАдоВназывается множество, состоящее из элементов множестваВ, не принадлежащихА. Дополнение обозначаетсяC=В-А(рис.3.1).

АВ

АВ

В-А

Рис. 3.1. Операции над множествами

6. Элементы теории графов

Граф задаётся парой множеств: множества Е, называемогомножеством вершин, и множества U, называемого множеством рёбер. Ребро u  Uесть пара(е_i, е_j), гдее_i, е_jЕ, указывающая, между какими двумя вершинами проведено ребро. Говорят, что реброuUинцидентно вершинаме_i, е_j. Если порядок рёбер не имеет значения, т.е.u= (е_i, е_j) = (е_j, е_i), то ребро называетсянеориентированным или просто ребром, если же порядок имеет значение, то реброu= (е_i, е_j) называетсяориентированным ребром илидугой. Вершинае_iназываетсяначалом дуги, е_j–конец дуги. Граф, содержащий хотя бы одну дугу, называетсяориентированным графом илиорграфом.

Граф G (E, U)называетсяконечным, если множество Е вершин конечно.

Граф G (E, U), у которого каждая вершинае_iЕсоединена рёбрами с остальными вершинами (любые две вершены соединены ребром), называетсяполным (рис.3.2).

Рис. 3.2. Полный граф

Если хотя бы две вершины соединены несколькими рёбрами, то такой граф называется мультиграфом. Две вершиные_i, е_j  Еназываютсясмежными, если они соединены ребром. Число рёбер, инцидентных данной вершинее_j,называетсялокальной степенью этой вершиныр(е_i). Число рёберrграфаG(E,U)определяется выражением.

где n– количество вершин в графе.

Рассмотрим граф, изображённый на рисунке 3.3.

Рис. 3.3. Ориентированный граф

Множество вершин графа состоит из пяти элементов: Е = {1, 2, 3, 4, 5}, а множество рёберU= {(1, 2), (1, 4), (1, 5), (2, 3), (3, 4), (5, 3)}. Ребро (5, 3) являетсяориентированнымребром или дугой. Число рёбер в графе определяется по значению локальных степеней для каждой вершины:

р(1) = 3;р(2) = 2;р(3) = 3;р(4) = 2;р(5) = 2;р= (3 + 2 + 3 + 2 + 2) / 2 = 6.

Важным в теории графов является понятие части графа G(E,U),который обозначаетсяG'(E',U')G(E,U). Множества вершин и ребёр части графа являютсяподмножествами вершин и рёбер исходного графаЕ'ЕU'U. Многие задачи на графах состоят в определении частей графа сзаданными свойствами.

Часть графа G'(E',U')G(E,U)называетсяподграфом графаG(E,U), еслиЕ' Е, а подмножествоU'Uобразовано только рёбрами, инцидентными вершинам множестваЕ'.

МаршрутомграфаGназывается последовательность рёберS= (u₁, u₂, , u _n), в которой каждые два соседних ребра имеют общую вершину, т.е. u₁ = (е₁, е₂); u₂= (е₂, е₃); ... u _n = (е_n, е_n+1).Не исключено, что одно и то же ребро может встречаться несколько раз на одном маршруте.

Две вершины е_iие_jназываютсясвязанными, если существует маршрут изе_iве_j.

Простой цепью, илипростым путём, называется маршрут, в котором ни одно ребро не повторяется дважды.Элементарной цепью илиэлементарным путём называется маршрут, в котором ни одна вершина не повторяется дважды.Циклом в графе называется маршрут, у которогоначальная вершина совпадает сконечной. Например, граф, представленный на рисунке3.4, имеет циклS= (1, 2, 3, 5, 4, 1).

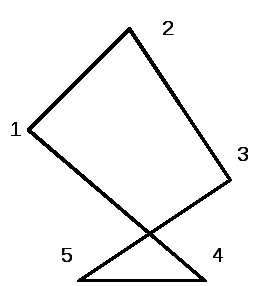
Рис. 3.4. Пример графа, имеющего цикл

Цикл, проходящий по всем рёбрам графа только один раз, называется эйлеровым циклом. В теории графов доказывается теорема, определяющая, содержит ли граф эйлеров цикл. Оказывается, конечный граф содержит эйлеров цикл тогда и только тогда, когда он связан, и все его локальные степени вершин чётные. Важной прикладной задачей теории графов является задача поиска в графе цикла, проходящего через каждую вершину только один раз. Такие циклы называютсягамильтоновыми циклами.

Весьма важным является связанный граф, не имеющий циклов, он называется деревом. В дереве любые две вершины связаны единственным путём. Вершина называетсяконцевой, если ей инцидентноне более одного ребра; одна из концевых вершин может быть выбрана в качестве корня.

Теория графов используется в информатике и программировании, например, для представления структур данных (деревья), для моделирования сетей (маршрутизации данных в Интернете). В теории алгоритмов, блок-схема алгоритма − это ориентированный граф, указывающий порядок исполнения команд. Вершины такого графа могут быть одного из трёх типов, представленных в таблице 11.

Таблица11