Определенный интеграл

Определенный интеграл является одним из основных понятий математического анализа и широко используется в разных областях науки, техники и в экономических исследованиях.

1. Задача вычисления площади криволинейной трапеции.

Пусть на отрезке[a, b]определена непрерывная функция у = f(х).Пустьf≥0для .

О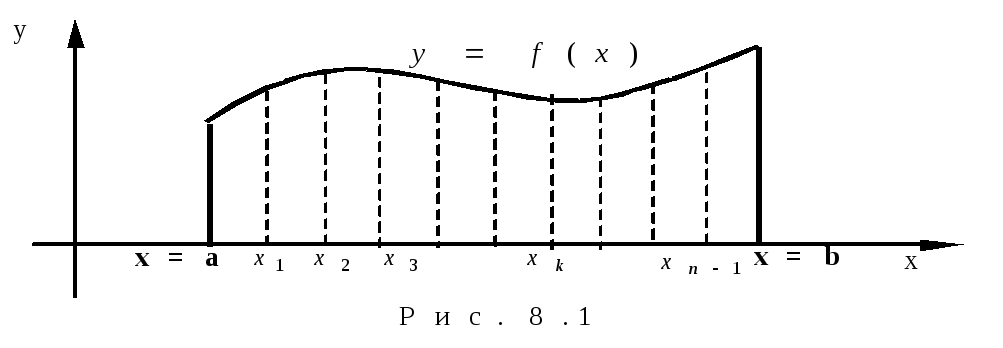пределение1. Криволинейной трапецией называется фигура, ограниченная прямыми х = а и х = b, отрезком [a, b]оси Ох и кривой у = f(х) (рис. 1).

Вычислим площадь этой криволинейной трапеции. С этой целью разобьем отрезок [a, b] произвольным образом на частей точками. Обозначим концы отрезка [a, b].Тогда отрезок [a, b]разобьется на отрезков

.

Обозначим их длины через . Через точки разбиенияпроведем перпендикуляры к осиОх и продолжим их к пересечению с кривой у = f(х). Эти перпендикуляры разделят площадь криволинейной трапеции на узких криволинейных трапеций. Заменим каждую из этих трапеций прямоугольником с основаниеми высотой, где. Площадь каждого такого прямоугольника равна. Сумма площадей всех таких прямоугольников будет равна

Таким образом, площадь S криволинейной трапеции приближенно равна этой сумме, то есть

. (8.1)

Эта формула будет тем точнее, чем меньше величина .

Чтобы получить точную формулу для вычисления площади S криволинейной трапеции, надо в этой формуле перейти к пределу, когда . Тогда

. (8.2)

Требование обеспечивает равномерность разбиения отрезка[a, b] на части.

Задача на вычисление пути, пройденного материальной точкой.

Пусть нужно определять путь , который прошла материальная точка, движущаяся по прямой с переменной скоростьюза время отдо.

Поделим промежуток времени напромежутков:. Обозначим черезпроизвольный момент времени из промежутка, а значения скорости в этой точке обозначимТочка, движущаяся с постоянной скоростьюна промежутке, проходит за это время путь, а за времяона пройдет путь

.

Путь, который проходит точка за время , вычисленный таким образом, будет отличаться от настоящего пути, но тем меньшее, чем меньше будет промежуток времени, тем меньшее изменяется скорость движения. Итак, когда, тогда переменная скорость на промежуткемало отличается от постоянной. Поэтому соответствующее действительности значение пути, пройденного точкой за время, будет равно пределу этой суммы при, т.е.

. (8.3)

3. Задача о работе переменной силы.

Пусть материальная точка , двигаясь прямолинейно под действием силыпрошла путьот точкидо точкив направления действия этой силы. Надо вычислить работу, силы

Если сила во время прямолинейного движения точкисохраняла постоянное значение, то искомая работа

.

Пусть теперь сила изменяется во время движения точкиМ, т.е. является функцией абсциссы точки М в системе координат, введенной таким образом, положительное направление оси совпадает с направлением движения точкиМ. Пусть абсциссы точек А и В соответственно и, т.о..

Разобьем отрезок произвольным чином наотрезков где -абсциссы точек распределения. Обозначим длины этих отрезков через .

Будем считать, что на каждом частичном отрезке сила сохраняет постоянное значение, которое она имеет в начале каждого отрезка:, тогда работа по перемещению материальной точки на каждом из отрезков будет равняться соответственно,

а вся работа приближенно определится как сумма

- дает приближенное значение работы, произведенной силой при перемещении материальной точки на путиАВ.

будет тем меньшее отличаться от , чем меньшими будут частичные отрезкитак как чем меньшее, тем меньшее успевает измениться значения силына этом промежутке. Поэтому точное значение работыми найдем, если перейдем к пределу суммыпри условии, что длины частичных отрезков направляются к нулю. Итак, имеем

. (8.4)

Рассмотрев три разных задачи, мы видим, что с математической точки зрения их решения, которые даются формулами (8.2-8.4), отображают одинаковую задачу .