Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет гражданской авиации

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

учебник Кузнецова 2003

.pdf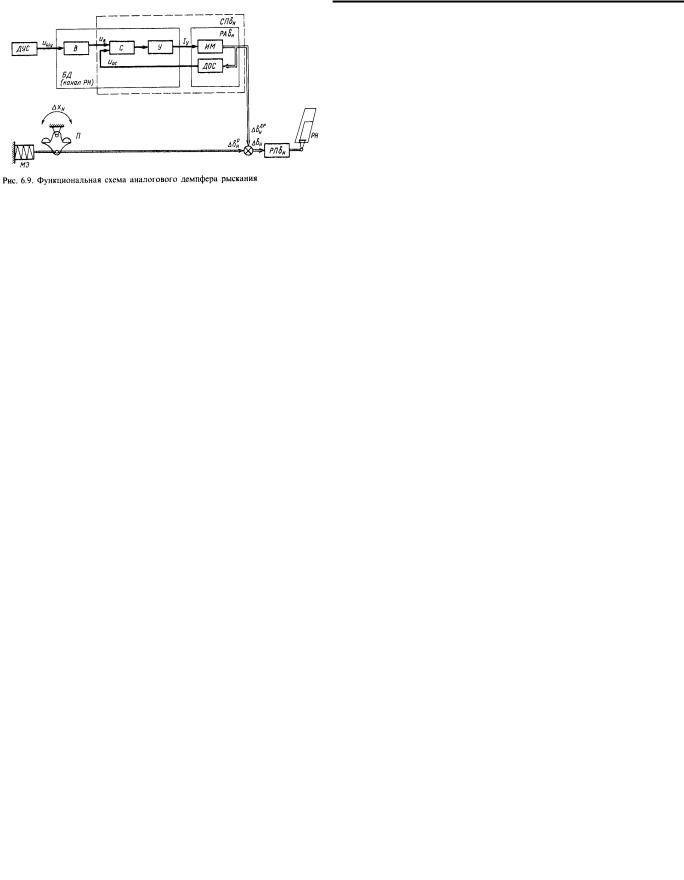

Скачиваний:

382

Добавлен:

22.03.2016

Размер:

9.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 189 10 11 12 13 14 15 16 17 18 > Следующая >>>

В.Г.Воробьев, С.В.Кузнецов АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ПОЛЕТОМ САМОЛЕТОВ

	ДК
W∆xэ (p) =	kш.эkωδэx		(6.77)
W∆xэ (p) =	p(TДКp +	1)	(6.77)
∆γ	p(TДКp +	1)	6.3. АВТОМАТИЧЕСКОЕ ДЕМПФИРОВАНИЕ КОЛЕБАНИЙ
	ω		6.3. АВТОМАТИЧЕСКОЕ ДЕМПФИРОВАНИЕ КОЛЕБАНИЙ
	x

Определим характеристики передаточных функций:	ПО РЫСКАНИЮ

aωx ,δэ

δxэ

kωδэx

δэДК

kωx

= −

aω

+ aω

kω

ωx +

δэ k

+ k

kδэ

,ω

,δ

ωx

ωx ωx

(6.78)

TДК = −

= −

Tωx

ωx

aω

,ω

+ aω ,δ

kω

ωx

δэ k

ωx

+ k

kδэ

ωx ωx

(6.79)

Таким образом, демпфер крена уменьшает постоянную времени по

угловой скорости крена TДК

< T , но вместе с этим и коэффициент

усиления

kωδэДК

< kωδэ .

На

рис.6.8 представлена

структурная схема

замкнутой системы "самолет-демпфер крена". Сворачивая эту схему можно получить передаточную функцию (6.76). Анализ этих передаточных функций показывает, что демпфер крена с законом управления (6.51) не влияет на их структуру, а лишь изменяет характеристики образующих звеньев.

Маневр самолета в боковой плоскости осуществляется энергичным отклонением пилотом баранки штурвала на величину ∆xэ . При этом

закон изменения ∆δэ = kш.э∆xэ близок к ступенчатому, то есть ∆xэ(t) =1(t)∆xэ и ∆xэ(p) = ∆x / p . На этапе быстрого бокового

кренового движения произойдет формирование нового установившегося значения угловой скорости крена

ДК

(ω

)ДК = lim[∆x

W∆xэ (p)] = lim{

p∆xэ

kш.эkωδэx

} =

уст

∆ωx

ДК

p +1

p→0

Tωx

= kωδэДК kш.э∆xэ . (6.80)

Так

как,

согласно

(6.78)

kωδэДК kш.э < kωδэ kш.э , то

(ωx )ДКуст < (ωx )уст . Реакция самолета на ступенчатое отклонение баранки штурвала описывается переходной функцией

ДК

∆ω

(p) =

∆xэ W∆xэ (p) =

kш.эkωδэx

∆x

. (6.81)

p(TДКp +

∆ωx

ωx

Перейдем от изображения к оригиналу

kш.эkωδэ

(1+kш.эkωδэ

)

−

∆ωx (t) =

−e

]∆xэ

(6.82)

1+ kш.эkδэ

ωx

Время переходного процесса tДКзат , по истечении которого отличие угловой скорости крена от установившегося значения будет равно 5%,

определяется		из	условия,	e	−tДК / TДК	= 0,05	откуда
					зат ωx
tДК	= −ln 0,05TДК 3TДК . Таким образом,					включение демпфера
зат		ωx	ωx

крена в проводку управления элеронами приводит к уменьшению времени переходного процесса, однако снижает эффективность поперечного управления от баранки штурвала.

6.3.1 Демпферы рыскания

Устройство и работа. В режиме ручного (штурвального) управления пилот наблюдает за рысканием самолета по указателю курсовой системы и воздействует на педали при возникновении колебаний таким образом, чтобы отклонение руля направления противодействовало бы этим колебаниям. Для освобождения пилота от решения этой задачи служат демпферы рыскания.

Демпфер рыскания (ДР) - средство автоматического управления, обеспечивающее демпфирование колебаний самолета по рысканию путем отклонения руля направления при возникновении угловой скорости рыскания.

Простейший демпфер, рыскания реализует следующий закон управления рулем направления:

∆δнДР = kωy ωy , (6.83)

где ∆δнДР - автоматическое отклонение руля направления от ба-

лансировочного положения демпфером рыскания; kωy - передаточный

коэффициент по угловой скорости рыскания, показывающий, на какой угол должен отклониться руль направления при изменении угловой скорости рыскания на 1°/с (1 рад/с).

Другими словами, отклонение руля направления демпфером рыскания пропорционально угловой скорости рыскания.

Демпферы рыскания применяются на самолетах с бустерной или электродистанционной системой управления, если собственная путевая устойчивость самолета неудовлетворительна. Исполнительные устройства сервоприводов демпферов рыскания-рулевые агрегаты включаются в механическую проводку управления по последовательной схеме. Поэтому общее отклонение руля направления от балансировочного

положения ∆δн равно сумме ручного отклонения руля направления

пилотом посредством педалей ∆δнР и автоматического отклонения

руля направления демпфером рыскания:

∆δн = ∆δнР +∆δнДР . (6.84)

Функциональная схема аналогового демпфера рыскания аналогична функциональным схемам демпферов тангажа и крена (рис. 6.9). Откло-

нение руля направления ∆δнР создается пилотом путем перемещения педалей П на величину ∆xн от балансировочного положения. С помощью дифференциальной качалки осуществляется суммирование этого сигнала с управляющим сигналом демпфера рыскания ∆δнДР .

Рулевой привод руля направления РПδн формирует отклонение руля направления.

При возникновении угловой скорости рыскания ωy датчик ДУС вырабатывает электрический сигнал uωy , пропорциональный этой

скорости. Вычислитель В вырабатывает управляющий сигнал uв согласно закону управления (6,83) на вход сумматора С сервопривода

15	май 2003г.

Tωy p

Глава 6. ДЕМПФИРОВАНИЕ КОЛЕБАНИЙ САМОЛЕТА

руля направления СПδн . Сервопривод преобразует этот сигнал в

перемещение штока рулевого агрегата руля направления ∆δнДР .

Влияние демпферов рыскания на путевую устойчивость и управляемость. Покажем, что с помощью демпфера рыскания улучша-

ется степень путевой статической устойчивости самолета mωy y . При

отклонении руля направления демпфером появляется приращение коэффициента момента рыскания

∆my = mδyн ∆δнДР = mδyн kωy ωy (6.85)

(ωy )ДРуст = const . Поэтому противодействие демпфера пилоту пре-

кращается, и расход перемещения педалей для создания угловой скорости не изменяется. При этом, естественно, ухудшаются характеристики устойчивости.

Кроме уменьшения неблагоприятного влияния на путевую управляемость демпферы рыскания с законом управления (6.89) и (6.90) устраняют негативные последствия взаимосвязи движений по рысканию и крену. Так, в установившемся развороте с креном демпфер рыскания с законом управления (6.83) противодействует развороту откло-

нением руля направления при возникновении угловой скорости ωy .

Возьмем частную производную выражения (6.85) по угловой ско-				Фильтрация постоянной составляющей этой скорости законами управ-
рости ωy :				ления (6.89) и (6.90) позволяет держать руль направления в нейтрали
ωy	δн			при совершении разворота и реагировать лишь на колебательность
		(6.86)		углового движения относительно постоянной составляющей скорости
∆my	= my kωy			разворота.
Следовательно, при включенном демпфере рыскания:
				Для дополнительного демпфирования самолета при заходе на по-
(mωy )ДР = mωy		+ mδн k	, (6.87)	садку, когда скорость самолета мала и эффективность руля направления
y	y	y	ωy	снижается, в закон управления (6.52) включается дополнительный
ω	ω			демпфирующий сигнал, пропорциональный угловой скорости рыска-
\| (my y )ДР \|>\| my y \| , (6.88)				ния,
т.е. степень путевой статической устойчивости самолета с демпфе-				ДР		Tωy p
ром рыскания выше, чем степень собственной путевой статической
				∆δн = kωy T p +1ωy + FАЗПkωy ωy , (6.91)
устойчивости самолета.
Покажем, что с помощью демпфера рыскания улучшается динами-						ωy
				где FАЗП	принимает значение, равное 1 при включении режима
ческая устойчивость бокового движения. На рис. 6.10, а представлены
переходные процессы, возникающие в результате ступенчатого откло-				автоматического захода на посадку (АЗП) и 0 во всех остальных режи-
нения пилотом руля направления на угол ∆δнР . Как видно из графиков				мах.
рис. 6.10б, демпфер рыскания уменьшает колебательность переходных				Структурная схема демпфера рыскания, реализующего закон
				управления (6.91), представлена на рис. 6.11. Таким образом, осуществ-
процессов по угловой скорости и углу рыскания - уменьшаются период				ляется демпфирование колебаний по рысканию с помощью системы
короткопериодических колебаний и время затухания. Так как отклоне-				АБСУ-154.
ние руля направления демпфером ∆δнДР вычитается из отклонения

руля направления пилотом ∆δнР , общее отклонение руля направления

∆δэ становится меньше. Это приводит к уменьшению установившего-

ся значения угловой скорости рыскания (ωДРy )уст по сравнению с

управлением без демпфера, т.е. эффективность управления рулем направления от педалей уменьшается.

На малых скоростях полета требуется дополнительное демпфирование самолета по рысканию при вхождении самолета в крен и при отклонении элеронов. Тогда в закон управления (6.90) включаются дополнительные сигналы, пропорциональные углу крена и углу отклонения элеронов, пропущенные через изодромные фильтры с постоян-

ными времени Tγ и Tδэ :

Особенности законов управления демпферов рыскания. Разно-

видностями демпферов рыскания являются демпферы, реализующие следующие законы управления:

∆δнДР = kωy ωy = kωy pωy ,

∆δнДР = kωy Tωy p +1 ωy (6.90)

В законе управления (6.89) управляющий параметр ωy - угловое

ускорение рыскания, получаемое дифференцированием в ДУС сигнала ωy . Изодромный фильтр Tωy p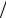(Tωy p +1) закона управления (6.90)

реализуется в вычислителе блока демпфера, например, с помощью RCцепочки.

Законы управления демпферов рыскания (6.89) и (6.90) позволяют уменьшить неблагоприятное влияние демпфера рыскания на путевую управляемость. Это достигается возвращением штока рулевого агрегата

Tω

T p

∆δДР = k

+ F {k

γ + k

δэ

} ,

ωy T p +1

γ T p

δэ T p +1

ЗАК

ωy

δэ

(6.92).

где FЗАК принимает значение, равное 1 при выпуске закрылков на

угол 30° и 0 при убранных закрылках.

Датчиком сигнала, пропорционального углу крена, служит гировертикаль ГВ. Датчиком сигнала, пропорционального углу отклонения элеронов, служит датчик обратной связи рулевой машины автопилота.

Датчиком выпуска закрылков является концевой выключатель КВ δзак .

Структурная схема демпфера рыскания, реализующего закон управления (6.92), представлена на рис. 6.12. Таким образом, осуществляется демпфирование колебаний по рысканию с помощью системы АССУ-86.

в нейтральное положение, когда ωy = 0 , т.е. ∆δнДР = 0 при

16	май 2003г.

− Mβ + Fβ Mδн kω

y zк y y

aωy ,β

Tωy p

В.Г.Воробьев, С.В.Кузнецов АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ПОЛЕТОМ САМОЛЕТОВ

Основной характеристикой боковой устойчивости самолета является степень путевой статической устойчивости по углу скольжения mβy .

Для ее увеличения и демпфирования боковых колебаний самолета в демпфере рыскания необходимо использовать сигнал, пропорциональ-

ный угловой скорости скольжения β . Однако создание датчиков такого сигнала затруднено, поэтому используют следующую упрощенную зависимость угловой скорости скольжения β от угловых скоростей

рыскания и крена в горизонтальном полете с постоянным углом атаки

α0 :

β = ωy cos α0 +ωx sin α0 . (6.93)

Следовательно, для эффективного демпфирования колебаний самолета по углу скольжения необходимо в демпфере рыскания помимо сигнала, пропорционального угловой скорости рыскания, вводить сигнал, пропорциональный угловой скорости крена. Тогда закон управления принимает следующий вид:

Рассмотрим модель быстрого бокового движения «чистого рыскания» по угловой скорости рыскания и углу скольжения (4.23) при наличии управляющих воздействий пилота на педали и включенном демпфере рыскания. Модель содержит уравнение состояния, уравнения выхода и входа, закон управления рулем направления ручного контура и закон управления рулем направления ручного контура и закон управления демпфера рыскания:

xбб(t) = Aббxбб(t) + Bббу uббу (t) , (6.96) yбб(t) = xбб(t) , (6.97)

uббу (t) = ∆δнр(t) +∆δнДР(t) , (6.98)

∆δнр(t) = Dббр ∆xн(t) , (6.99)

∆δнДР(t) = DббДР∆yбб(t) . (6.100)

Параметры модели определяют так:

∆ωy (t)

Aбб

aωy ,ωy

aωy ,β

xбб(t) =

∆β(t)

aβ,ω

aβ,β

Bу

aω

,δ

Dр

= k

, DДР

=[k

0] . (6.101)

н ,

ш.н

бб

ωy

Подставим уравнения выхода (6.97), входа (6.98) и законы управления (6.99) и (6.100) в уравнение состояния (6.96) и выполним преобразование Лапласа при нулевых начальных условиях:

(Ip − Aбб −Bббу DббДР)Yбб(p) = Bббу Dббp ∆Χн(p) . (6.102)

Получим вектор передаточных функций замкнутой системы «само- лет-демпфер рыскания» в быстром боковом движении по рысканию и скольжению на отклонение пилотом педалей при включенном демпфере рыскания:

∆δнДР = kωy Tωy p +1 ωy + kωx ωx , (6.94)

где kωx = kωx sin α0 .

Таким образом, анализ одного из простейших средств автоматизации бокового движения самолета показывает необходимость учета взаимодействия движений рыскания и крена.

Так как сигналы с ДУС, пропорциональные угловым скоростям, содержат помехи, то для их фильтрации применяется апериодический

фильтр с постоянной времени Tф = 0,1−0, 2с.

Закон управления имеет вид

ДР

Tωy p

∆δн

{kω

ωy + kω

(δзак)

ωx } .

T p

p +1

Передаточный коэффициент kω

(6.95)

корректируется по положению

закрылков (принимает большее значение при выпущенных закрылках и уменьшается при убранных).

Структурная схема демпфера рыскания, реализующего закон управления (6.95), представлена на рис.6.13. Так осуществляется демпфирование колебаний по рысканию с помощью демпфера рыскания ДР62.

6.3.2. Моделирование демпфирования колебаний по рысканию

WДР(p) =	Yбб(p)	=

бб	∆Xн(p)

= (Ip − Aбб −Bббу DббДР)−1Bббу Dббp = ФббДР(p)Bббу Dббp . (6.103) где ФббДР(p) = (Ip − Aбб −Bббу DббДР)−1 = (φббДР(p))−1 - пере-

ходная матрица состояния быстрого бокового движения самолета, управляемого демпфером рыскания.

Элементами вектора WббДР(p) являются передаточные функции самолета по параметрам быстрого бокового движения «чистого рыскания» на управляющее воздействие пилота ∆Χн(p) :

ДР

= [W

∆xн

(p)

∆xн

(p)] (6.104)

(p)]

бб

∆ωy

∆β

Переходная матрица состояния

{φДР(p)}

пр

ΦббДК (p) =

бб

(6.105)

φббДР(p)

Определитель матрицы

φббДР(p)

(p −aβ,β −aωy ,δн kωy

) −aωy ,β

−aβ,ωy

(p −aβ,β )

(6.106)

= p2 + 2hбДРp + (ωбДР)2 = ∆ДР(p).

Коэффициент демпфирования и частота боковых короткопериодических колебаний самолета, управляемого демпфером рыскания:

hбДР = −

(aω

+aβ,β +aω ,δ kω

) = −

ωy y +

zβ

δyн kω ) ,

,ω

y н y

(6.107)

(ωбДР)2 = aωy ,ωy aβ,β −aβ,ωy aωy ,β +

ωy

+aβ,βaωy ,δн kωy = My

Fzк

Присоединенная матрица

{ΦДР(p)}

(p −aβ,β )

aβ,ω

(p −aβ,β

бб

пр

. (6.108)

−aωy ,δн kωy ) . (6.109)

Тогда переходная матрица состояния

17	май 2003г.

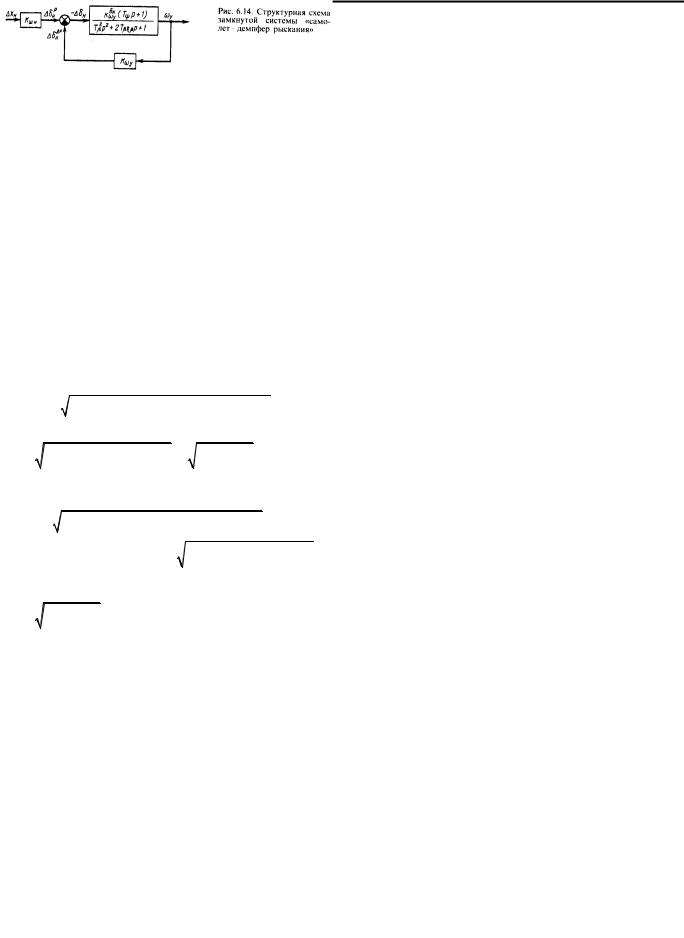
Глава 6. ДЕМПФИРОВАНИЕ КОЛЕБАНИЙ САМОЛЕТА

ΦббДР(p) =

(p −aβ,β )

aωy ,β

∆

(p)

∆

(p)

. (6.110)

ДР

(p −aβ,β −aω

aβ,ω

,δ

kω

)

∆ДР(p)

∆ДР

(p)

а вектор передаточных функций самолета

kш.нaωy ,δн (p −aβ,β )

∆

(p)

WДР

(p) =

ДР

(6.111)

бб

ш.нaωy ,δн aβ,ωy

∆ДР(p)

или

kδнДР (T p +1)

W∆xн (p) =

ωy

, (6.112)

(TДР)2 p2 +

∆ωy

ДРξДРp +1

W∆xн (p)

kβδнАБУ

. (6.113)

(TАБУ)2 p2 + 2T

ξАБУp +

∆β

АБУ

Время и относительный коэффициент демпфирования боковых короткопериодических колебаний самолета, управляемого демпфером рыскания:

TДР =

aω

,ω

aβ,β −aβ,ω

aω

,β + aβ,βaω

,δ

kω

Tβ

, (6.114)

ωy

−

δв k

1+ kω

kδн

ξДР

= −

ω ,ω

β,β

+ a

,δ

)

y y

aωy ,ωy aβ,β −aβ,ωy aωy ,β + aβ,βaωy ,δн kωy =

ωy

= −

+ M

− M

н k

ωy

)

−M

+ M

н k

zк

ωy

δн T ω

ωy

, (6.115)

+ k

δн

ωy

ДР

δн

(ω

)

= ω

(1+ k

) . (6.116)

(TДР)2

ωy

Коэффициенты усиления самолета, управляемого демпфером рыскания:

ДР			kωδн
kωδнy	=		y			, (6.117)
		1	+ kω kωδн
				y	y
δДР	=		kβδн
kβн						. (6.118)

		1	+ kω	y	kωδн
					y

На рис. 6.14 представлена структурная схема замкнутой системы «самолет-демпфер рыскания». Сворачивая эту схему, можно получить передаточную функцию (6.112).

Таким образом, демпфер рыскания с законом управления (6.83) не влияет на вид передаточных функций, но изменяет характеристики

образующих их звеньев. Анализ выражений (6.114)-(6.118) показывает, что демпфер рыскания положительно влияет на характеристики колеба-

тельного звена передаточных функций. Постоянная времени TβДР

уменьшается, частота собственных колебаний ωβДР и относительный коэффициент затухания ξβДР увеличиваются. Однако при этом умень-

шаются коэффициенты усиления kωδнДР	и kβδнДР .
y

Для снижения негативного влияния демпфера рыскания на путевую управляемость сигнал угловой скорости ωy в законе управления (6.90)

пропускается через изодромный фильтр.

Рассмотрим работу демпфера рыскания с изодромным законом управления (6.90) по демпфированию колебаний различной частоты. Передаточная функция демпфера имеет вид

W	∆ω	y (p) =	∆δ	н		(p)	= k		Tωy p	. (6.119)
						(p)		ωy T p +1
∆δн			∆ω		y
									ωy

Представим передаточную функцию (6.119) в несколько ином виде, поделив числитель и знаменатель на Tωy :

∆ωy (p) = k

. (6.120)

ωy p +

∆δн

ωy

Из

(6.120)

видно,

что

при

мы имели бы

ωy

∆ωy (p) k

ωy

, т.е. «идеальный»

демпфер рыскания. Это условие

∆δн

выполняется при больших частотах колебания, когда после замены

p = jω :

W∆ωy (jω) = k		jω			(6.121)
	ωy jω+			1
∆δн
			T
				ωy

и второе слагаемое в знаменателе (6.121) мало по сравнению с первым. Тогда

∆δн( jω) kωy ωy ( jω) , (6.122)

т.е. при высокочастотных колебаниях демпфер рыскания отклоняет руль направления пропорционально угловой скорости рыскания, что от него и требуется. При малых частотах колебаний демпфер рыскания

начинает работать как дифференцирующее звено, так как при ω → 0

k		jω		→ k		T jω . (6.123)
k			1	→ k		T jω . (6.123)
	ωy jω+		1		ωy	ωy
	ωy jω+		T
			ωy

Когда ω → 0 , а ωy → const и ωy → 0 , выходной сигнал

изодромного фильтра и управляющий сигнал демпфера рыскания будут стремиться к нулю. В результате при развороте с постоянной скоростью демпфер рыскания воздействовать на руль направления не будет.

Довороты самолета в боковой плоскости, а также устранение скольжения осуществляются энергичным отклонением пилотом педа-

лей на величину ∆xн . При этом закон отклонения руля направления

∆δн = kш.н∆xн близок к ступенчатому. На этапе быстрого бокового

движения происходит формирование нового установившегося значения угловой скорости рыскания:

					kδнДР (T p +1)
= lim{			p∆xн			ωy		ψ	}
				p (TβДР)2 p2
p→0								+ 2TβДРξβДРp +1
(∆ω	y	)ДР		= lim[p∆x		н	(p)W∆xн (p)] =
		уст		p→0				∆ωy

18	май 2003г.

В.Г.Воробьев, С.В.Кузнецов АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ПОЛЕТОМ САМОЛЕТОВ

ДР		kωδн kш.н
= kш.нkωδн	∆xн =	y				∆xн . (6.124)
= kш.нkωδн	∆xн =	+ k		δ		∆xн . (6.124)
y	1	+ k	ω	kωн
				y	y
Так как	согласно		(6.117) kш.нkωδнДР				< kωδн kш.н , то
						y	y

(∆ωy )ДРуст < (∆ωy )уст . Это показано на рис. 6.8. Реакция самолета на

ступенчатое отклонение педалей описывается переходными функциями:

∆ω

ДР

(p) = p∆x

(p)W

∆xн

(p)

∆ωy

∆x

δнДР

(Tψp +1)

, (6.125)

kωy

+ 2T

ДРξДРp +1]

[(TДР)2 p2

∆xн

δнДР

∆n

ДР

(p) =

Fzк

kωy ,β

. (6.126)

[(T

ДР)2 p2 + 2TДР

ξДРp +1]

Перейдем от изображения

∆nДР(p) к оригиналу:

ДР

ξДР

V0Fβ kδн

−

ДР

∆n

(t) =

zк

ωy ,β

[1−

Tβ

1−(ξβДР)2

sin(

1−(ξДР)2

+arcsin

1−

(ξДР)2 )]∆x

TДР

Выражение (6.127) определяет переходный процесс в боковом короткопериодическом колебательном движении самолета с демпфером рыскания при отклонении педалей пилотом. Анализ выражения (6.127) показывает, что оно аналогично выражению (6.43) для нормальной перегрузки. Динамические характеристики боковой устойчивости и управляемости определяются аналогично (6.44). Таким образом, включение демпфера рыскания в проводку управления рулем направления приводит к уменьшению колебательности процесса управления, однако снижает эффективность путевого управления от педалей.

19	май 2003г.

ной нормальной перегрузке.

Влияние автоматов продольной устойчивости на устойчивость и управляемость. Покажем, что с помощью автомата продольной устойчивости повышается степень продольной статической устойчивости по перегрузке. Влияние демпферной части закона управления (7.3) на характеристики продольной устойчивости и управляемости показано в § 6.1. Рассмотрим влияние составляющей закона управления по избы-

май 2003г.

uωz

и uny , что приведет к плавному возвращению самолета к исход-

друга, АПУ вернет руль высоты в балансировочное положение. Дальнейшая отработка руля будет вызвана сменой знака суммы сигналов

В.Г.Воробьев, С.В.Кузнецов АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ПОЛЕТОМ САМОЛЕТОВ

Г л а в а 7

где ∆δвАПУ -

отклонение руля высоты автоматом продольной ус-

АВТОМАТИЧЕСКОЕ УЛУЧШЕНИЕ УСТОЙ-

тойчивости;

∆α = α −α0 -

приращение

угла атаки относительно

ЧИВОСТИ И УПРАВЛЯЕМОСТИ

опорного значения, имевшего место в момент включения автомата;

Если самолет обладает неудовлетворительными характеристиками

∆ny = ny −1 - избыточная нормальная перегрузка; kα - передаточ-

ный коэффициент по приращению угла атаки, показывающий, на какой

устойчивости и управляемости или эти характеристики существенно

угол должен отклониться руль высоты при изменении угла атаки на 1°;

меняются по режимам полета, возникает задача их улучшения с помо-

kny

-передаточный коэффициент по избыточной нормальной пере-

щью соответствующих автоматических средств.

В качестве средств автоматического улучшения устойчивости са-

грузке, показывающий, на какой угол должен отклониться руль высоты

молета применяют автоматы устойчивости, среди которых различают

при изменении избыточной нормальной перегрузки на единицу.

автоматы продольной устойчивости и автоматы боковой устойчивости.

В связи с недостаточной точностью датчиков угла атаки и необхо-

Их общей особенностью является отклонение руля при возникновении

димостью создания специальных схем для запоминания опорного зна-

перегрузок относительно соответствующей связанной оси самолета.

чения угла атаки закон управления (7.1) большого распространения не

Разделение средств автоматического демпфирования и улучшения

получил. Поэтому обычно используется закон управления (7.2), кото-

устойчивости самолета на автоматы демпфирования и устойчивости

рый часто комплексируется с законом управления демпфера тангажа:

достаточно условно, так как демпфирование и устойчивость - взаимо-

∆δАПУ = k

∆ω + k

∆n

. (7.3)

связанные свойства самолета. Кроме того, на современных самолетах

автоматы демпфирования и устойчивости комплексируются в единой

То есть отклонение руля высоты автоматом продольной устойчиво-

системе и работают одновременно и согласованно.

сти пропорционально угловой скорости тангажа и избыточной нор-

Автоматическое улучшение управляемости самолета осуществля-

мальной перегрузке.

ется путем отклонения рулей средствами автоматического управления

Благодаря последовательному включению исполнительного уст-

при воздействии пилота на рычаги управления и изменения параметров

ройства автомата в механическую проводку бустерной или электродис-

короткопериодического движения самолета либо изменением кинема-

танционной системы управления рулем высоты при совместном управ-

тики системы управления рулями по режимам полета. Благоприятное

лении самолетом пилотом и автоматом полное отклонение руля высоты

влияние автоматики на характеристики управляемости проявляется в

от балансировочного положения ∆δв

равно алгебраической сумме

улучшении качества и обеспечении стабильности переходных процес-

сов выхода самолета на новый режим полета после целенаправленного

∆δ

= ∆δP

+∆δАПУ .

воздействия пилота на рычаги управления. При этом сохраняются тре-

буемые характеристики демпфирования и устойчивости.

В состав автомата продольной устойчивости (рис.7.1) входят дат-

В качестве средств автоматического улучшения управляемости са-

чик линейного ускорения ДЛУ, датчик угловой скорости ДУС, вычис-

молета применяют автоматы управления, автоматы регулирования

литель ВАПУ и сервопривод руля высоты СПδв Автомат продольной

управления и загрузки, автоматы триммирования.

устойчивости работает следующим образом. При изменении нормаль-

Среди автоматов управления различают автоматы продольного

управления и бокового управления. Их общей особенностью является

ной перегрузки на вход вычислителя В с датчиков ДУС и ДЛУ посту-

дополнительное к ручному автоматическое отклонение руля при воз-

пают сигналы uω

и un

. Сигнал un

преобразуется в сигнал u∆n

действии пилота на рычаги управления. При наличии на самолете бус-

терной системы управления автоматическое отклонение руля суммиру-

ется с ручным отклонением руля посредством механической проводки.

При наличии на самолете электродистанционной системы управления

автоматическое отклонение руля суммируется с электродистанционным

отклонением. Иногда автомат управления сам представляет собой элек-

тродистанционную систему управления и берет на себя все ее функции.

На современных самолетах автоматы управления комплексируются с

автоматами демпфирования и устойчивости в единой системе и рабо-

тают одновременно и согласованно.

Эти

сигналы

суммируются

согласно

закону

управления (7.3).

Среди автоматов регулирования управления различают автоматы

Управляющий сигнал

uσ

вызывает отработку сервоприводом руля

регулирования продольного, путевого и поперечного управления. Ана-

логичным образом классифицируют автоматы регулирования загрузки.

высоты.

При

отклонении

руля

высоты

на

угол

∆δвАПУ возникает

Общая особенность этих автоматов - обеспечение постоянства статиче-

ских характеристик управляемости при изменении режимов полета

управляющий аэродинамический момент

Mzδв

, противоположный по

путем воздействия на кинематику механической проводки управления.

7.1. АВТОМАТИЧЕСКОЕ УЛУЧШЕНИЕ УСТОЙЧИВОСТИ

знаку возмущению. Поэтому угловая скорость

ωz

и избыточная нор-

ПО ПЕРЕГРУЗКАМ

мальная перегрузка начнут уменьшаться, а вместе с ними и сигналы

uω

с ДУС и un

с ДЛУ.

Когда угловая скорость тангажа станет

Устройство и работа автоматов продольной устойчивости. Ав-

равной нулю ( ωz

= 0 ), руль высоты все еще будет отклонен автома-

томаты демпфирования не полностью решают проблему улучшения

пилотажных свойств самолета, так как компенсируют лишь недоста-

том

продольной

устойчивости

благодаря еще

имеющемуся

сигналу

точное собственное демпфирование самолета. Вследствие действия

uny

с ДЛУ (тогда как демпфер тангажа в этот момент возвращал руль

внешних продольных возмущений, даже при включенном демпфере

тангажа, у самолета могут измениться угол атаки и нормальная пере-

высоты в балансировочное положение). Поэтому угловая скорость

грузка. Поэтому необходимо сохранить исходный режим полета по

тангажа

поменяет знак и избыточная перегрузка ∆n

начнет

углу атаки и нормальной перегрузке. Для освобождения пилота от ре-

шения этой задачи служат автоматы продольной устойчивости.

интенсивно уменьшаться. Когда сигналы uω

и un

уравновесят друг

Автомат продольной устойчивости (АПУ) - средство автоматиче-

ского управления, обеспечивающее повышение устойчивости самолета по углу атаки и нормальной перегрузке на всех этапах полета путем отклонения руля высоты при возникновении приращения угла атаки или избыточной нормальной перегрузки.

Простейшие автоматы продольной устойчивости реализуют следующие законы управления рулем высоты:

∆δвАПУ = kα∆α , (7.1)

∆δвАПУ = kny ∆ny , (7.2)

Глава 7. АВТОМАТИЧЕСКОЕ УЛУЧШЕНИЕ УСТОЙЧИВОСТИ И УПРАВЛЯЕМОСТИ

точной нормальной перегрузке.

При отклонении руля высоты автоматом продольной устойчивости появляется приращение коэффициента момента тангажа

∆mz = mδzв ∆δвАПУ = mδzв kny ∆ny .

С учетом того, что на малых углах атаки ∆ny = kαny ∆α , где kαny

- коэффициент пропорциональности, степень продольной статической устойчивости по перегрузке самолета, управляемого АПУ, определится согласно (3.30) следующим образом:

АПУ		dmRz		kny mδzв	АПУ
σп	= (		)V=const = σп +		= σп +∆σп .
σп	= (	dcya	)V=const = σп +	cya	= σп +∆σп .
		dcya		cya

Так как mδzв < 0 , то приращение степени продольной статической устойчивости по перегрузке при использовании автомата продольной устойчивости ∆σпАПУ < 0 . Следовательно, σпАПУ > σп .

указателем угла скольжения, отклоняет руль направления. Разворот при этом становится координированным. Для освобождения пилота от решения этой задачи служат автоматы боковой устойчивости.

Автомат боковой устойчивости (АБУ) - средство автоматического управления, обеспечивающее повышение устойчивости самолета по углу скольжения и боковой перегрузке на всех этапах полета путем отклонения руля направления при возникновении приращения угла скольжения или боковой перегрузки.

Простейшие автоматы боковой устойчивости реализуют следующие законы управления рулем направления:

∆δнАБУ = kβ∆β (7.4)

∆δнАБУ = −knz nz (7.5)

где ∆δнАБУ - отклонение руля направления автоматом боковой ус-

тойчивости; ∆β = β−β0 - приращение угла скольжения относительно опорного значения; kβ , knz -передаточные коэффициенты по прира-

Покажем, что с помощью автомата продольной устойчивости			щению угла скольжения и боковой перегрузке ( nz0 = 0 ).
улучшается динамическая устойчивость	продольного	движения. Как	Невысокие точностные характеристики известных датчиков угла
видно из рис. 7.2, характеристики динамической устойчивости самолета
			скольжения не позволяют широко применять закон управления (7.4).
с АПУ - период колебаний T , и время затухания tк		~ уменьшаются.	Поскольку углы скольжения обычно малы, то боковая перегрузка прак-
к	зат		тически пропорциональна углу скольжения. Так как измерение боковой
Автомат продольной устойчивости так же, как и демпфер тангажа,
позволяет снизить колебательность продольного короткопериодическо-			перегрузки не вызывает затруднений, закон управления (7.5)
го движения самолета и уменьшить длительность переходных процес-			распространен более широко.
сов. Вместе с тем увеличивается частота продольных короткопериоди-			Обычно автомат боковой устойчивости объединяется с демпфером
			рыскания и имеет закон управления
ческих колебаний νк .			∆δнАБУ = kω ωy − kn	nz . (7.6)
			y	z

При совместном управлении пилотом и автоматом полное отклонение руля направления от балансировочного положения равно алгебраической сумме

Величина νк , зависит от запаса статической устойчивости самоле-

та по перегрузке, который в течение полета меняется в широких пределах. При этом увеличение запаса устойчивости ухудшает демпфирование. Демпферная часть закона управления (7.3) увеличивает коэффици-

ент демпфирования hк и попутно способствует некоторому увеличе-

нию частоты собственных колебаний νк . Составляющая закона управ-

ления по перегрузке также увеличивает частоту νк . Таким образом,

подбором передаточных коэффициентов kωz и kny удается снизить

запас статической устойчивости по перегрузке, компенсируя смещение фокуса вперед обратной связью по перегрузке.

Другим важным преимуществом автоматов продольной устойчивости является их способность возвращать самолет к исходному режиму полета по нормальной перегрузке. При длительном возмущении появляется статическая ошибка в виде установившегося значения избыточ-

ной перегрузки ∆ny.уст . Поэтому АПУ с законами управления (7.2) и

(7.3) называют статическими. Для ликвидации статической ошибки применяют более сложные законы управления, например с интегрированием сигнала с датчика ДЛУ.

Основной недостаток автомата продольной устойчивости - уменьшение эффективности управления рулем высоты от колонки штурвала,

так как отклонение руля высоты автоматом ∆δвАПУ вычитается из

отклонения руля высоты пилотом ∆δвр . Это приводит к уменьшению

интенсивности вертикального маневра.

Устройство и работа автоматов боковой устойчивости. Демпфе-

ры крена и рыскания не могут противодействовать изменению угла скольжения и боковой перегрузки. Поэтому наряду с задачей демпфирования боковых короткопериодических колебаний возникает задача сохранения исходного режима полета по углу скольжения и боковой перегрузке. Особенно это актуально при развороте, когда пилот воздействует на элероны. Для противодействия возникающему при этом скольжению и связанной с ним боковой перегрузке пилот, наблюдая за

∆δн = ∆δнр +∆δнАБУ .

Функциональная схема автомата боковой устойчивости аналогична схеме АПУ. Отличие заключается в том, что датчик угловой скорости ДУС ориентирован по измерительной оси OY, а датчик линейных ускорений ДЛУ - по измерительной оси OZ. Вычислитель ВАБУ вырабаты-

вает управляющий сигнал uσн согласно закону управления (7.6) на основе сигналов uωy и unz . Автомат содержит сервопривод руля

направления СПδн . Работа АБУ аналогична работе АПУ.

Влияние автоматов боковой устойчивости на устойчивость и управляемость. Покажем, что с помощью автомата боковой устойчивости повышается степень путевой статической устойчивости по углу

скольжения mβy . Демпферная часть закона управления (7.6) обеспечи-

вает увеличение степени путевой статической устойчивости по угловой скорости рыскания mωy y . Рассмотрим влияние составляющей закона

управления по боковой перегрузке.

При отклонении руля направления автоматом боковой устойчивости появляется приращение коэффициента момента рыскания

∆my = mδyн ∆δнАБУ = −mδyн knz ∆nz .

Известно, что при малых углах скольжения nz = −kβnz ∆β, где

kβnz - коэффициент пропорциональности. Тогда приращение частной

производной коэффициента момента рыскания по углу скольжения

∆mβy = mδyн knz kβnz ∆β .

Следовательно, при включенном автомате боковой устойчивости:

(mβy )АБУ = mβy + ∆mβy , (mβy )АБУ > mβy .

Анализ влияния автомата боковой устойчивости на динамические характеристики бокового движения аналогичен проведенному анализу для АПУ. Недостатком автомата боковой устойчивости является уменьшение эффективности путевого управления.

Особенности законов управления автоматов продольной и бо-

ковой устойчивости. Для обеспечения астатизма управления при длительных внешних возмущениях в закон управления АПУ вводят сигнал,

22	май 2003г.

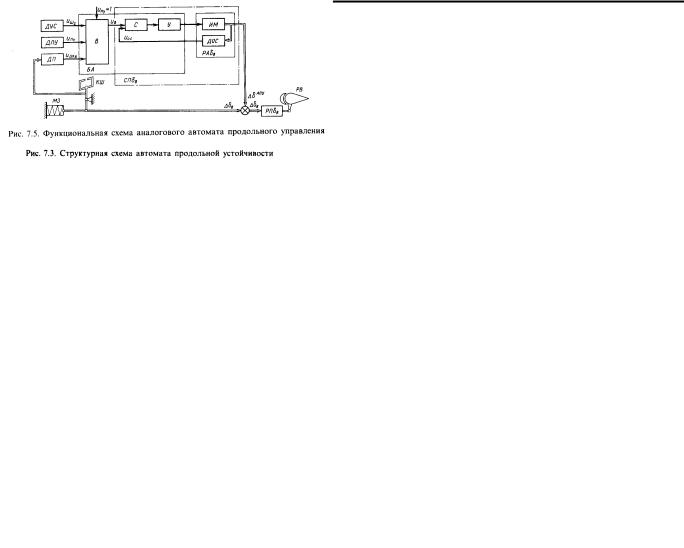
В.Г.Воробьев, С.В.Кузнецов АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ПОЛЕТОМ САМОЛЕТОВ

пропорциональный интегралу от избыточной нормальной перегрузки

(рис. 7.3):

k∫n

∆δ

= k

ω + k

∆n

, (7.7)

ωz T p +1 z

где

k∫ny

- передаточный коэффициент по интегралу от избыточ-

ной нормальной перегрузки.

Для ликвидации статической ошибки автоматов боковой устойчивости по углу скольжения при длительных внешних возмущениях применяется интегрирование сигнала с датчика ДЛУ либо использование скоростной обратной связи в сервоприводе автомата:

p∆δн = kωy ωy − knz nz . (7.8)

Тогда в законе управления (7.8) вместо сигнала угловой скорости ωy следует использовать ее производную ωy для сохранения демп-

фирующих свойств автомата (рис. 7.4). Так обеспечивается улучшение путевой устойчивости с помощью систем САУ-62 и САУ-86.

7.2. АВТОМАТИЧЕСКОЕ УЛУЧШЕНИЕ ПРОДОЛЬНОЙ УСТОЙЧИВОСТИ И УПРАВЛЯЕМОСТИ

7.2.1. Автоматы продольного управления

Устройство и работа. Демпферы тангажа и автоматы продольной устойчивости обладают одним общим недостатком: снижают эффективность продольного управления самолетом от колонки штурвала. Если, к тому же, самолет обладает неудовлетворительными характеристиками продольной управляемости, пилоту приходится компенсировать снижение эффективности продольного управления дополнительным отклонением колонки штурвала и руля высоты. Автоматы продольного управления служат для освобождения пилота от решения этой задачи.

Автоматы продольного управления (АПУ) - средства автоматиче-

ского управления, обеспечивающие улучшение продольной управляемости самолета на всех этапах и во всех режимах полета путем отклонения руля высоты при воздействии пилота на колонку штурвала.

Простейший автомат продольного управления реализует следующий закон управления рулем высоты:

∆δвАПУ = kхв ∆xв , (7.9)

где ∆δвАПУ - автоматическое отклонение от балансировочного по-

ложения руля высоты автоматом продольного управления; kхв - пере-

даточный коэффициент по отклонению колонки штурвала, показывающий, на какой угол должен отклониться руль высоты при перемещении пилотом колонки штурвала от балансировочного положения на 1мм;

∆xв - отклонение пилотом колонки штурвала.

Обычно автомат продольного управления объединяется с демпфером тангажа или автоматом продольной устойчивости. Тогда их совме-

стные законы управления имеют следующий вид:

∆δвАПУ = kωz ∆ωz + kxв ∆xв ; (7.10)

∆δвАПУ = kωz ∆ωz + kny ∆ny + kxв ∆xв . (7.11)

Последовательное включение исполнительного устройства автомата в механическую проводку бустерной или электродистанционной системы управления рулем высоты позволяет суммировать отклонения руля высоты пилотом и автоматом.

Рассмотрим функциональную схему аналогового автомата продольного управления, включенного в бустерную систему управления (рис.7.5.). В состав автомата входят датчик угловой скорости тангажа ДУС, датчик линейных ускорений ДЛУ, датчик положения колонки

штурвала ДП, вычислитель В и сервопривод руля высоты СПδв . Вы-

числитель и электронная часть сервопривода образуют электронный блок автомата БА в канале руля высоты.

Автомат продольного управления работает следующим образом. При отклонении пилотом колонки штурвала КШ датчик ДП вырабаты-

вает электрический сигнал u∆xв , пропорциональный ∆xв . Этот сиг-

нал преобразуется в вычислителе В согласно закону управления (7.11) в сигнал uσв , который вызывает отработку сервоприводом руля высо-

ты. Полное отклонение руля высоты равно ∆δвP +∆δвАПУ . Отклонение руля высоты вызовет появление управляющего аэродинамического момента Mzδв , который изменит угловую скорость тангажа ωz и

избыточную нормальную перегрузку ∆ny . Сигналы, пропорциональ-

ные этим параметрам uωz и u∆n y поступят с датчиков ДУС и ДЛУ

на вычислитель, и вызовут уменьшение сигнала uв . Тогда сервопривод вернет шток рулевого агрегата в нейтральное положение. В это время угловая скорость тангажа ωz и избыточная перегрузка ∆ny

примут новые установившиеся значения, пропорциональные отклонению руля высоты пилотом с помощью колонки штурвала. При возвращении пилотом колонки штурвала в балансировочное положение все процессы повторяются в обратном порядке.

Влияние автоматов продольного управления на характеристи-

ки управляемости самолета. Автоматы демпфирования и устойчивости обладают одним общим недостатком - снижают эффективность ручного управления самолетом, увеличивая градиенты перемещений

(xвnУ )ДТ и усилий (PвnУ )ДТ на колонке штурвала. Поэтому демп-

ферная составляющая kωz ωz и составляющая перегрузки kn y ∆ny

законов управления (7.10)-(7.11) вызывают тот же эффект. Использование сигнала ∆xв в АПУ приводит к увеличению значения коэффициента штурвала в силу того, что

∆δв = ∆δвP +∆δвАПУ = kш.в∆xв + kxв ∆xв + kωz ωz + kn y ∆ny = = kш/ .в∆xв + kωz ωz + kn y ∆ny ,

где kш/ .в = kш.в + kxв .

Такое увеличение коэффициента штурвала компенсирует уменьшение градиентов перемещения и усилий, так как

23	май 2003г.

Глава 7. АВТОМАТИЧЕСКОЕ УЛУЧШЕНИЕ УСТОЙЧИВОСТИ И УПРАВЛЯЕМОСТИ

(xny )

δвny

= (xny

)

АПУ

kш/

.в

kш.в

ДТ

(Pny )

δвny

Pxв

δвny

Pxв

= (Pny )

kш.в

АПУ

kш/

.в

ДТ

Таким образом, автомат продольного управления позволяет сохранить статические характеристики продольной управляемости в заданных пределах.

Влияние автомата продольного управления на динамические характеристики видно из рис.7.6. Демпферная часть закона управления автомата обеспечивает уменьшение колебательности короткопериодического движения по угловой скорости тангажа, делая его почти апериодическим. Составляющая закона управления АПУ, пропорциональная

отклонению колонки штурвала ∆xв , обеспечивает равенство устано-

вившегося значения угловой скорости (ωz )уст установившемуся зна-

чению угловой скорости без применения автоматики. Тем самым сохраняется эффективность продольного управления.

Особенности законов управления автоматов продольного управления. В аналоговых автоматах продольного управления получил распространение закон управления

∆δвАПУ = kωz ωz + kxв (1− k/xв )∆xв . (7.12)

Передаточный коэффициент по отклонению колонки штурвала k/xв зависит от ее балансировочного положения следующим образом:

kx/	=	∆xв.бал.0 +∆xв.бал	,
в		(xвnУ )зад

где ∆xв.бал.0 - постоянное отклонение колонки штурвала, харак-

терное для данного самолета ∆xв.бал - отклонение колонки штурвала

из нейтрального положения в балансировочное (xвnУ )зад - заданный

для данного самолета градиент перемещения колонки штурвала на единицу нормальной перегрузки.

Величины ∆xв.бал.0 и ∆xв.бал являются постоянными и реали-

зуются в вычислителе в виде соответствующих опорных напряжений. Для измерения отклонения колонки штурвала из нейтрального положения в балансировочное устанавливается дополнительный датчик поло-

жения ДП. Наиболее просто сигнал, пропорциональный ∆xв.бал ,

можно получить, измеряя отклонение штока механизма эффекта триммирования МЭТ. Механизм используется пилотом для снятия усилий с колонки штурвала и ее перемещения в балансировочное положение. Тогда в функциональной схеме рис.7.5 появляется еще один датчик ДП

с электрическим выходом u∆xв.бал .

Автомат с законом управления (7.12) позволяет сохранить постоянство статических характеристик продольной управляемости самолета в различных режимах полета. Так обеспечивается улучшение продольной устойчивости и управляемости самолета Ту-154 с помощью системы АБСУ-154-2 (рис.7.7).

Пример 7.1. Рассчитаем характеристики управляемости самолета с автоматом продольного управления, имеющим закон управления (7.12) для исходных данных примеров 3.1, 3.2, и 6.1.

В начале полета ∆xв.бал = ∆δв.бал / kш.в = −90 мм, где

∆δв.бал = −8D, k/xB = (∆xв.бал.0 +∆xв.бал) / xвnУ зад = −0,915 ,

где		∆xв.бал.0 = −20 мм,				xвnУ зад =120 мм,
(xвnУ )АПУ = (xвnУ )ДТ /(1−kx/ в ) = −145 мм,
(PnУ )	АПУ	= (xnУ )	Pxв + P = 214 H.
в	АПУ	в	АПУ в	0
В	конце		полета	∆δв.бал = −8D , ∆xв.бал = −20 мм,
(xnУ )	АПУ	= −126 мм, (PnУ )		АПУ	=191 H.
в	АПУ		в	АПУ

Таким образом, автомат продольного управления существенно снизил разброс значений характеристик управляемости по режимам полета, сделав их практически постоянными. Так, градиент перемещения колонки штурвала теперь меняется от -145мм в начале полета до - 126мм в конце полета, а градиент усилий на колонке штурвала меняется от 214H в начале полета до 191Н в конце полета, что практически незаметно для пилота.

Влияние отказов автомата продольного управления на управ-

ление продольным движением. Пассивный отказ автомата продольного управления по сигналу ∆xв приводит к прекращению отработки

руля высоты через контур автоматического управления при воздействии пилота на колонку штурвала. Эффективность продольного управления самолетом падает, градиенты перемещений и усилий на колонке штурвала возрастают.

Полный пассивный отказ автомата, комплексированного с демпфером тангажа приводит к снижению эффективности демпфирования продольных короткопериодических колебаний и возрастанию эффективности продольного управления.

Активный отказ автомата продольного управления аналогичен активному отказу демпфера тангажа и сопровождается отработкой штока рулевого агрегата на максимальный ход, ограниченный концевыми выключателями. Ограничение хода штока рулевого агрегата АПУ сказывается на эффективности продольного управления, особенно при вертикальном маневре, когда часть рабочей зоны отклонения руля высоты расходуется демпферной составляющей автомата.

Цифроаналоговые автоматы продольного управления. Ужесто-

чение требований к характеристикам продольной устойчивости и управляемости самолета и, как следствие, усложнение законов управления АПУ, привели к необходимости реализации автоматов на цифроаналоговой схемотехнике.

В состав автомата входят датчики положения колонки штурвала ДП, угловой скорости тангажа ДУС и нормальной перегрузки ДЛУ, аналоговый блок управления БУ, цифровой вычислительный блок ус-

тойчивости и управляемости БВУУ и рулевой агрегат высоты PAδв

(рис.7.8).

Формирование закона управления осуществляется одновременно в аналоговом вычислителе В блока управления БУ и цифровом вычисли-

24	май 2003г.

В.Г.Воробьев, С.В.Кузнецов АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ПОЛЕТОМ САМОЛЕТОВ

те БВУУ. При этом аналоговый закон управления реализует функции автомата продольной устойчивости по сигналам нормальной перегрузки и угловой скорости тангажа.

Цифровой закон управления выполняет собственно функции АПУ по сигналам отклонения колонки штурвала, а так же сигналам и разовым командам от смежных систем и датчиков. Сигналы с датчиков ДП, ДУС и ДЛУ являются аналоговыми - напряжений постоянного и пере-

менного тока u∆xв , uωz и u∆ny . Часть сигналов со смежных датчи-

ков также имеют аналоговую форму. Ряд сигналов со смежных систем поступает в виде последовательного биполярного кода. Разовые команды подаются в виде напряжения постоянного тока 27 В.

Аналоговые сигналы и разовые команды преобразуются в БВУУ к цифровому виду. Управляющее воздействие формируется в цифровом

виде с последующим преобразованием в аналоговый сигнал uσцв . Этот

сигнал подается в блок управления, где суммируется с управляющим сигналом uσав аналогового контура. Сервопривод АПУ СПδв фор-

мирует отклонение руля высоты ∆δвАПУ .

В случае отказа цифрового контура продолжает работать аналоговый контур с сохранением основных функций демпфирования колебаний самолета по тангажу и устранения избыточной перегрузки.

Управляющее воздействие АПУ ∆δвАПУ суммируется с управ-

ляющим воздействием ручного контура ∆δPB электродистанционной

системы управления по усилию на колонке штурвала.

В обобщенном виде закон управления такого АПУ выглядит следующим образом:

∆δвАПУ = σaв +σцв ,

σaв = σωвz +σв∆ny ,

σцв = σв∆xв +σв∆α +σвM +σвАНУПС +σСАДв ,

σωвz = kωz ωz , σв∆ny = k∆ny ∆ny ,

σв∆xв = kxв (ϕ) ∆xв ,

Txв p +1

σв∆α = Fзакkα (∆α,M)[α −αD(M)] ,

σвM = Fзакδв(M) ,

σвАНУПС = FАНУПСδвАНУПС(∆xв , ∆ny ,α) , σСАДв = FСАДδСАДв (∆nУ) . (7.13)

Составляющая закона управления по угловой скорости тангажа

σωвz обеспечивает демпфирование колебаний самолета по тангажу. Составляющая закона управления по избыточной нормальной пере-

грузке σв∆ny улучшает продольную устойчивость самолета. Составляющая закона управления по отклонению колонки штурва-

ла σв∆xв улучшает продольную управляемость самолета, причем пере-

даточный коэффициент kxв корректируется по углу отклонения ста-

билизатора ϕ , а сигнал ∆xв пропускается через апериодический фильтр с постоянной времени Txв .

Составляющая закона управления по приращению угла атаки σв∆α обеспечивает улучшение продольной устойчивости и ограничение угла атаки при убранных закрылках. Требуемое значение угла атаки α0 корректируется по числу М. Передаточный коэффициент корректируется по разности ∆α = α −α0 и числу М. Составляющая закона

управления по числу M σвM обеспечивает ограничение скорости поле-

та самолета путем дополнительного отклонения руля высоты при изменении числа М при убранных закрылках.

При включении автомата непосредственного управления подъемной силой (АНУПС) формируется составляющая закона управления

σвАНУПС , которая корректируется по отклонению колонки штурвала,

избыточной перегрузке, приращению угла атаки и управляющему воздействию вычислительной системы управления полетом. Назначение и особенности формирования этой составляющей будут рассмотрены в гл.8.

При включении системы активного демпфирования (САД) форми-

руется составляющая закона управления σСАДв , которая корректиру-

ется по избыточной нормальной перегрузке. Назначение и особенности формирования этой составляющей будут рассмотрены в главе 8.

Так обеспечивается улучшение устойчивости и управляемости продольного движения с помощью системы АСУУ-96 (рис.7.9).

Распространен также вариант реализации цифроаналогового АПУ (рис.7.10) без суммирования управляющих воздействий аналогового и цифрового контуров. Отличие этой схемы заключается в том, что основным контуром управления является цифровой. Аналоговый автоматический контур, а также ручной контуры подключаются к сервоприводу электродистанционной системы управления только при отказе цифрового контура. Контроль и коммутация производится в аналоговых блоках управления и контроля БУК.

В обобщенном виде закон управления такого АПУ выглядит следующим образом:

∆δвАПУ = σaв σцв ,

σaв = σваωz +σва∆ny +σва∆xв ,

σцв = σвц∆xв +σвц∆α +σвцny + σωвцz + σψвц ,

σваωz = kωz ωzф ,

25	май 2003г.

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 189 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.03.2016513.22 Кб17УР курсовик заочники 2008.pdf
#
08.02.20153.43 Mб16Устав ЛетяГА.doc
#
22.03.2016528.9 Кб26Учеб пособ АиУ ч 1.doc
#
20.08.20194.02 Mб24учебник по русскому_0.doc
#
08.12.20193.04 Mб4Учебник (1).doc
#
22.03.20169.51 Mб382учебник Кузнецова 2003.pdf
#
22.03.201618.82 Mб188Учебник по ВС.DOC
#
21.04.2019710.14 Кб14Учебник по ФИЛОСОФИи ТЕХНИКИ.doc
#
10.01.20202.85 Mб0Учебное пособие КМЗИ ч1 СКС.doc
#
10.01.20202.71 Mб1Учебное пособие КМЗИ ч2 АСКС.doc
#
22.03.2016953.99 Кб81Учебное пособие. Инновационный менеджмент.2007.pdf