логистика кр1,2 (2) вариант3

Контрольная работа №1.

Задание для первой контрольной работы.

Предприятию для нормальной работы требуется ежедневно А=2 тонн материалов. Материалы можно получить со склада двумя способами: либо на транспорте склада, либо на транспорте предприятия. Склад выделяет транспорт грузоподъемностью В=12 тонн раз в неделю, собственный транспорт предприятия может доставлять материалы непрерывно интенсивностью С=7 тонн в сутки в течение D=2 первых дней в неделю. Стоимость еженедельной доставки груза складом – с_В=25 д.е., предприятием – с_С=12 д.е. стоимость хранения материалов на предприятии без учета срока хранения - с_ХО=5 д.е. за тону в сутки. Ежедневные потери, связанные с дефицитом материалов, - с_n=16 д.е. за сутки. Найдите недельный расходы за использование материалов в обоих случаях. Постройте графики движения материалов. Выберите наименьший по расходам вариант доставки груза.

Решение.

1. Рассмотрим случай доставки материалов транспортного склада. Поставка в этом случаи будет мгновенной. В зависимости от количества поставляемого материала может быть два случая:

1. когда материала больше потребного на неделю;

2. когда материала меньше недельной потребности.

В качестве исходных данных для расчета послужат данные варианта №3.

Вариант	Ежедневное потребление материалов	Грузоподъемность транспорта склада	Интенсивность доставки своим транспортом	Период доставки своим транспортом	Стоимость доставки складом	Стоимость доставки предприятием	Стоимость хранения, независимая от срока	Стоимость хранения, зависимая от срока	Потери от дефицита
	А, тонн в сутки	В, тонн	С, тонн в сутки	D, сутки	сb, д.е.	сс, д.е.	схо, д.е. за тонну	схт, д.е. за тонну в сутки	сn, д.е. за сутки
3	2	12	7	2	25	12	5	-	16

Недельный график поступления и расхода материала с учетом доставки со склада представлен на рис. 1.

Количество привезенного товара хватит на 12/2=6 дней. Площадь под графиком представляет собой площадь треугольника:

При заданной стоимости хранения с_ХО=5 д.е./тонна необходимо определить среднее количество хранимого материала L:

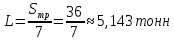
Так как стоимость хранения не зависит от времени хранения, то стоимость хранения равна:

Доставленные складом материалы обеспечивают работу производства в течении 6 дней. Следовательно , количество дней, не обеспеченных ресурсом, составляет 1 день:

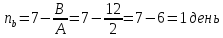
При этом расходы из – за дефицита материала составляет:

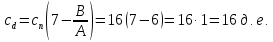
Стоимость транспортировки составляет с_В=25 д.е. с учетом расходов из-за дефицита материала суммарная стоимость доставки складом и хранения ресурса составляет:

2. Рассмотри случай доставки материалов транспортом предприятия (рис.2)

Для определения среднего количества хранимого материала определим площадь под ломаной кривой. Площадь состоит из трапеции и треугольника (рис. 2). Высота трапеции – 1 сутки; высота треугольника – 6 суток. Стороны трапеции – С=7, С-А=5; основание треугольника – 2С-А=12. Тогда площадь ломаной кривой равна:

Стоимость хранения:

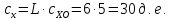
Доставка транспортом предприятия в точности обеспечивает недельный запас материалов (к концу недели запас равен нулю). Дополнительных расходов из-за дефицита материала нет (с_d=0).

Тогда суммарная стоимость доставки транспортом предприятия и хранения материала:

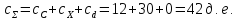
Сравнение стоимости доставки материалов складом или предприятием показывает, что доставка транспортом предприятия выгоднее: 66,715>42.

Контрольная работа №2

Задание для второй контрольной работы.

Предприятию известно поведение спроса от цены. Его можно описать аналитически:

Где Y – спрос (в единицах продукции),

x – цена единицы продукции,

a, b – коэффициенты (приведены в табл. приложения 3).

По номеру варианта a=-5, b=0,7.

Необходимо найти доход предприятия как функцию цены и определить максимальный доход и цену, при которой он реализуется.

Второй вопрос: как следует изменить существующую цену (х_сущ=8), чтобы получить максимальный доход?

Решение.

Выполнение работы начнем с построения графика спроса. На оси абсцисс нанесем цену – х, на оси ординат – величину спроса Y. График показан на рис. 3. Рассчитанные значения координат для построения графика приведены в таб.1

Таб.1 Зависимость спроса от цены.

x	Y	x	Y	x	Y	x	Y
0	0,9933	5	0,8176	10	0,1192	15	0,0041
1	0,9866	6	0,69	11	0,063	16	0,002
2	0,9734	7	0,525	12	0,0323	17	0,001
3	0,9478	8	0,3543	13	0,0163	18	0,0005
4	0,9002	9	0,2142	14	0,0082	19	0,0002

Как известно, доход находится как произведение цены на количество реализованной продукции. Считая, что спрос определяет реализованную продукцию, можно определить величину дохода Р:

График дохода как функция цены показан на рис. 4. Рассчитанные значения координат для построение графика приведены в табл. 2.

Таб. 2. Зависимость дохода от цены

х	Р	х	Р	х	Р	х	Р
0	0	5	4,088	10	1,192	15	0,0615
1	0,9866	6	4,14	11	0,693	16	0,032
2	1,9468	7	3,675	12	0,3876	17	0,017
3	2,8434	8	2,8344	13	0,2119	18	0,009
4	3,6008	9	1,9278	14	0,1148	19	0,0038

Доход является функцией одной переменной – х. нахождение экстремума такой функции, в данном случае максимума, не представляет труда. Следует найти первую произвольную по х и приравнять ее к нулю. Она равна:

Достаточно положить численность равным нулю, то есть

Решение данного уравнения можно осуществить с помощью Excel. Т.е. средства Excel позволяет найти цену, при которой реализуется максимальный доход:

Ответ на первый вопрос задания: при цене х = 6,61 доход максимальный, который равен:

Ответ на второй вопрос задания: существующую цену следует снизить с 8 до 5,61 д.е.