1.5. Полный кпд гтд прямой реакции

Полным КПД ГТД прямой реакции называется отношение тяговой работы

ко всей теплоте, внесенной в двигатель с топливом, т. е.

. (1.11)

Так как Q_о характеризует величину химической энергии топлива при условии его полного сгорания в двигателе и при отсутствии потерь тепла через стенки камеры сгорания, то полный КПД оценивает долю этой энергии, преобразованную в тяговую работу. Значит, он наиболее полно учитывает все виды потерь в процессе преобразования химической энергии топлива в тяговую работу двигателя по перемещению летательного аппарата.

Введем понятие внутреннего КПД ТРДД

.

В отличие от внутреннего КПД термодинамического цикла 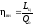он учитывает гидравлические потери в наружном контуре ТРДД, что следует из сравнения выражений для

L_ц = иL_тм =

Тогда для полного КПД ТРДД получим

η_п = η_{вн ТРДД} η_тяг,

т. е. полный КПД ТРДД равен произведению внутреннего КПД ТРДД и тягового КПД.

В ТРД L_тм=L_ц, поэтому внутренний КПД ТРД совпадает с внутренним КПД термодинамического цикла.

Полный КПД характеризует экономичность двигателя в полете в отличие от удельного расхода топлива, который характеризует экономичность двигателя только при заданной скорости полета и данном типе топлива.

При работе двигателя на месте полный КПД равен нулю, т. к. равен нулю тяговый КПД. В полете полный КПД может достигать значений 0,2…0,35 и более.

Найдем связь между полным КПД и удельным расходом топлива, который, как известно, равен

.

Для этого заменим в выражении для удельного расхода топливавеличину удельной тяги значением, определенным из формулы (1.11) для полного КПД, и учитывая, что

,

получим

.

Тогда окончательно будем иметь

. (1.12)

Таким образом, при заданной скорости полета удельный расход топлива обратно пропорционален полному КПД. Значит, оценивать экономичность двигателей путем сравнения их удельных расходов топлива можно только при одинаковой скорости полета. Поэтому С_уд является менее универсальным параметром, характеризующим экономичность двигателя, чем полный КПД. Однако С_уд позволяет оценить экономичность двигателя в стартовых или стендовых условиях. При этом используется следующая зависимость:

.

1.6. Оптимальное распределение работы цикла между контурами в трдд без смешения потоков

При разработке ТРДД возникает вопрос, как распределить работу цикла между контурами, чтобы получить максимальную удельную тягу двигателя.

Передача работы воздуху наружного контура осуществляется с помощью компрессора низкого давления, который принято называть вентилятором. Изменять величину этой работы можно за счет изменения степени повышения давления в КНД . (Часто вместоиспользуют символили ). При изменении будет изменяться и величина работы

,

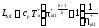потребная для привода во вращение КНД. Поэтому необходимо изменять и работу расширения газа в турбине, которая передается частично в наружный контур. Таким способом можно управлять распределением работы цикла

L_ц = (1.13)

между контурами.

Например, увеличение работы L_е =mL_кII, передаваемой из внутреннего контура в наружный, как следует из выражения

, (1.14)

будет приводить к увеличению скорости истечения воздуха с_сII из сопла наружного контура (рис.1.13), а в соответствии с (1.13) при заданной величине L_ц – к уменьшению скорости истечения газов из сопла внутреннего контура. Это вызовет изменение тяги двигателя

Р=P_I+P_II=G_вIP_удI+G_вIIP_удII,

Рис. 1.13. Схема двухконтурного

двигателя с раздельными контурами

создаваемой обоими контурами вместе. В этом выражении P_удI=(c_cI– V) – удельная тяга внутреннего, а P_удII= (c_cII– V) – удельная тяга наружного контура. В соответствии с этим удельная тяга двигателя с раздельными контурами определяется по формуле

. (1.15)

Оптимальным распределением работы цикламежду контурами двухконтурного двигателя будем считать такое, при котором его удельная тяга достигает максимума.

Определим это распределение при условии, что L_ц, m, η_II и V неизменны, а изменяется лишь L_кII, т. е. величина работы, передаваемой из внутреннего контура через вентилятор воздуху, протекающему через наружный контур. Для этого возьмем производную от функции (1.15) по L_кII и, приравняв ее к нулю, получим следующее условие максимума Р_уд

. (1.16)

Из формул (1.13) и (1.14) при принятых выше условиях следует, что

и.

Подставив значения этих производных в выражение (1.16), получим

. (1.17)

Таким образом, при оптимальном распределении L_ц между контурами с_сII = η_IIс_сI , причем с_сII тем меньше с_сI, чем ниже η_II, т. е. чем выше гидравлические потери в наружном контуре. При отсутствии гидравлических потерь в наружном контуре (η_II= 1), оптимальному распределению работы цикла между контурами соответствует равенство скоростей истечения газа и воздуха из этих контуров. При принятых допущениях максимальной удельной тяге соответствует минимальный удельный расход топлива, поскольку

, (1.18)

а величины g_т=G_т/G_вI и m не изменяются.

Определим значение степени повышения давления в вентиляторе , соответствующее оптимальному распределению работы цикла между контурами. Для этого установим, как от зависят скорости истечения газа и воздуха, удельная тяга и удельный расход топлива двигателя.

Увеличение приводит к повышениюL_кII, а значит в соответствии с формулой (1.14) – к возрастанию скорости истечения воздуха из наружного контура с_сII (рис. 1.14). Но при этом увеличивается и величина работы L_е = mL_кII, передаваемой из внутреннего в наружный контур, что при неизменной L_ц в соответствии с формулой (1.13) приводит к уменьшению с_сI. Как видно из рисунка, при увеличении 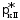удельная тяга вначале возрастает и достигает максимального значения прис_сII= η_ІІс_сI. Это значение и является оптимальным. Дальнейшее увеличениеуже приводит к снижениюР_уд. Удельный расход топлива в соответствии с формулой (1.18) изменяется обратно пропорционально Р_уд.

Такой характер изменения Р_уд объясняется изменением потерь кинетической энергии со струями газа и воздуха, покидающими двигатель. Это приводит к изменению тягового КПД двигателя, характеризующего, как отмечалось выше, эффективность преобразования работы цикла в тяговую работу.

Рис. 1.14. Влияние наРудиСуд ТРДД(Н= 0; МН=0; σвх= 1;m= 1; = 25;Тг* = 1600;= 0,84)				Рис.1.15. Влияние m и Н на (=25;Т*г=1600 К;=0,84)

Скорости истечения газа и воздуха из сопел внутреннего и наружного контуров двигателя соответственно равны

, .

Так как температура воздуха в наружном контуре за вентилятором значительно ниже температуры газов за турбиной, то, как видно из формул и из рис. 1.14, для получения равных или близких по величине скоростей истечения газа с_сI и воздуха с_сII давление за вентилятором должно быть значительно выше давления за турбиной.

Значение (илиL_кIIопт) для ТРДД с раздельными контурами зависит от многих факторов. Влияние наиболее важных из них можно проанализировать, приняв для упрощения η_ІІ = 1. Тогда оптимальному распределению работы между контурами будет соответствовать равенство скоростей истечения из этих контуров, т. е. с_сI= с_сII, и из формул (1.13) и (1.14) получим

. (1.19)

Таким образом, любой фактор (π, Δ, η_с, η_р, Т^*_в), приводящий к изменению работы цикла, а значит и L_кIIопт , приводит к изменению . Например, увеличение высоты полета при неизменном значении температуры перед турбиной ведет к увеличениюL_ц за счет увеличения Δ=Т^*_г/Т_н и в соответствии с формулой (1.19) – к увеличению L_кIIопт и, следовательно, . Увеличение степени двухконтурности приводит к уменьшениюL_кIIопт и соответственно (рис.1.15).