1.4. Обобщенное уравнение бернулли

Если из уравнения сохранения энергии

вычесть уравнение первого закона термодинамики ,

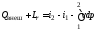то получим следующее уравнение

Это уравнение называется обобщенным уравнением Бернулли. Оно показывает, что подведенная к газу внешняя работа расходуется на его политропическое сжатие, изменение кинетической энергии и преодоление гидравлического сопротивления.

1.5. Теорема эйлера об изменении количества движения

Рис. 1.10. Силы, действующие

на профиль в потоке

При проектировании газотурбинных двигателей, анализе их рабочего процесса и расчете эксплуатационных характеристик возникает необходимость определения сил взаимодействия газа с элементами двигателя, находящимися в потоке (например, при определении усилий, действующих на лопатки компрессора и турбины, силы тяги, создаваемой двигателем, и т.д.)

Рассмотрим аэродинамический профиль, обтекаемый потоком (рис. 1.10).

Вектор аэродинамической силы , действующей на этот профиль, можно определить, интегрируя силы давленияи трения, с которыми газ действует на поверхностьf этого профиля, т.е.

.

Очевидно, что профиль воздействует на газ с силой , равной по величине, но противоположно направленной, т.е.= –.

Рис. 1.11. К объяснению

теоремы Эйлера

Однако определение силы интегрированием сил давления и трения газа в инженерной практике затруднительно, т.к. значения и распределение этих сил по поверхности обтекаемого тела довольно сложно определить.

Но, если использовать теорему Эйлера об изменении количества движения газового потока при обтекании тела, то аэродинамическую силу, действующую на тело, можно определить без знания и во всех точках обтекаемой поверхности.

Примем, что движение газа установившееся. Выделим произвольной поверхностью F некоторый объем газа, окружающий обтекаемое тело, например, профиль. Такую поверхность обычно называют контрольной поверхностью. На рис. 1.11 показано плоское сечение этой поверхности.

Отбросим газ вне контрольной поверхности и заменим его действие на газ внутри этой поверхности силами давления и трения.

Тогда в соответствии с теоремой Эйлера, при установившемся течении газа сумма всех газодинамических сил (сил давления и трения), действующих на выделенную произвольной контрольной поверхностью F массу газа со стороны отброшенного вне этой поверхности газа и обтекаемых тел, равна разности количеств движения вытекающей из этой поверхности и втекающей в неё в единицу времени масс газа, т.е.

.

Здесь сумма сил, действующих на массу газа, находящегося внутри контрольной поверхности со стороны самой контрольной поверхности,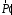сила, действующая на этот газ со стороны обтекаемого тела (профиля),разность количеств движения вытекающей из этой поверхности и втекающей в неё в единицу времени масс газа.

Рациональным выбором формы контрольной поверхности можно облегчить вычисление как этих газодинамических сил, так и количеств движения вытекающей и втекающей в единицу времени масс газа.

Сила, действующая на обтекаемое тело (профиль), = –.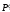