Вопросы экзаменационных билетов по математике за 1 семестр. Элементы линейной и векторной алгебры.

1. Матрицы: определение-Матрицами называются массивы элементов, представленные в виде прямоугольных таблиц, для которых определены правила математических действий. Элементами матрицы могут являться числа, алгебраические символы или математические функции. ,

элемент матрицы-Элементы матрицы обозначаются , где - номер строки, в которой находится элемент, а - номер столбца ,

размерность матрицы- Пара чисел I и J называется размерностью матрицы и обознается как I×J

2. Квадратная- Если число столбцов матрицы равно числу ее строк (I = J = N), то такая матрица называется квадратной ,

симметричная-Матрица A называется симметричной, если At = A. Иными словами aij = aji , диагональная-Матрица называется диагональной, если все ее элементы, кроме диагональных (aii) равны нулю ,

единичная- Единичной матрицей (обозначается I, а иногда E) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1 ,

треугольная-Матрица A называется верхней треугольной, если все ее элементы, лежащие ниже диагонали, равны нулю ,

трапецевидная- это матрица элементы главной диагонали , которой не равны нулю ,

нулевая матрица- Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается O. Очевидно, что A+O = A, A−A = O и 0A = O .

Равные матрицы - Две матрицы называются равными, если они имеют одинаковые размеры .

3. Действия над матрицами:

транспонирование- Матрицу можно транспонировать. При этой операции матрица переворачивается, т.е. строки и столбцы меняются местами. Транспонирование обозначается штрихом, A' или индексом At ,

сложение -две матрицы одинаковой размерности можно поэлементно складывать и вычитать ,

умножение на число -Матрицы можно умножать на числа. При этом каждый элемент умножается на это число .

Свойства сложения и умножения на число- Свойства умножения матрицы на число:

1.   

2.   

3.   

4.   

5.   

Свойства сложения и вычитания матриц:

1.   Ассоциативность 

2.   , где 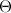 - нулевая матрица соответствующего размера.

3.   

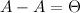
4.   Коммутативность 

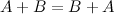
4. Умножение матриц- Матрицы можно перемножать, но только в том случае, когда они имеют соответствующие размерности .

5. Многочлены от матриц- (прочитать -http://www.reshim.su/blog/mnogochlen_ot_matricy/2013-06-26-336).

6. Определители 2-го и 3-го порядка - . Их вычисление.-

7. Свойства определителей-

1 При транспонировании квадратной матрицы её определитель не меняется:  .

2  Общий множитель в строке можно выносить за знак определителя

3

4  Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем

5 Если две строки определителя поменять местами, то определитель поменяет знак

6 Определитель с двумя равными строками равен нулю

7 Определитель с двумя пропорциональными строками равен нулю

8 Определитель, содержащий нулевую строку, равен нулю

9  Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число

10 Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов

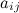8. Минор элемента определителя- Минором  к элементу  определителя 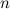-го порядка называется определитель -го порядка, полученный из исходного вычеркиванием -той строки и -того столбца .

Алгебраическое дополнение элемента определителя - Алгебраическим дополнением  к элементу  определителя -го порядка называется число .

Разложение определителей по строке или столбцу- Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения .