
Курс лекций по физике - Часть_2 - Электрическое_и_магнитное_поле_Оптика
.pdf
В о л н о в о й п о в е р х н о с т ь ю называют поверхность, в точках которой колебания имеют одинаковую фазу.
Форма волновой поверхности в однородных изотропных средах совпадает с формой волнового фронта.
Рассмотрим классификацию волн, исходя из определения волны.
По характеру периодического процесса волны бывают с к а л я р н ы е , когда невозможно указать пространственное направление колебаний (волна температуры) и
ве к т о р н ы е , когда колебания происходят в определенном направлении (колебание частиц воздуха в звуковой волне). При этом сам колеблющийся параметр также может быть скалярным (давление в звуковой волне) или векторным (напряженность электрического поля в электромагнитной волне).
По частотным характеристикам волны делятся на две группы:
|
м о н о х р о м а т и ч е с к и е в о л н ы – распространяется гармоническое |
|
колебание с частотой ω ; |
|
н е м о н о х р о м а т и ч е с к и е в о л н ы – одновременно распространяют- |
|
ся различные колебания с разными частотами. |
По природе волны делятся на:
м е х а н и ч е с к и е – распространение упругих (механических) колебаний вещества (например, звук).
э л е к т р о м а г н и т н ы е – распространение колебаний электромагнитного поля (например, свет).
В зависимости от направления колебаний волны делятся на два типа:
п р о д о л ь н ы е в о л н ы – колебания происходят вдоль направления распространения волны (например, звук);
направление распространения волны
направление колебаний
п о п е р е ч н ы е в о л н ы – колебания происходят перпендикулярно распространению волны, такая волна называется (например, электромагнитные волны).
направление распространения волны
направление колебаний
Среди волн по форме волнового фронта выделяют:
с ф е р и ч е с к и е в о л н ы – волновой фронт является сферой. Например, излучение точечного источника в однородной изотропной среде.
Волновой фронт

п л о с к и е в о л н ы – волновой фронт является плоскостью.
Волновой
фронт
Направление
распространения
волны
Волновые процессы описываются волновым уравнением, решением которого они являются.
Вспомним колебания. Уравнение свободных гармонических колебаний имеет вид
|
d 2 x |
ω2 x 0 . |
|
|
|
|
dt 2 |
0 |
|
|
|
Его решением является функция, описывающая гармонический колебательный |
||
процесс x(t) x0 cos(ω0t φ) . |
|
|
В о л н о в о е у р а в н е н и е имеет несколько похожий вид, оно представляет со-
бой дифференциальное уравнение второго порядка в частных производных
2ξ |
V 2 |
ξ 0 |
или |
ξ |
1 |
2ξ |
. |
|
t 2 |
V 2 |
t 2 |
||||||
|
|
|
|
|
Здесь греческой буквой ξ («кси») обозначен колеблющийся параметр, – дифферен-
циальный оператор Лапласа (P. Laplace, 1749–1827), для которого используется гре-
ческая буква «дельта» (не путать с приращением). Поскольку ξ(r ,t) является
функцией нескольких переменных, уравнение записывается не в полных производных, как для колебаний, а в частных производных.
Используемый дифференциальный оператор Лапласа можно представить через
другой дифференциальный оператор 2 . Дифференциальный оператор («набла») определяется в декартовой системе координат как формальный вектор с проек-
|
|
|
|
|
|
|
|
|
|
|
|
|
||
циями |
|
, |
|
, |
|
|
или i |
|
|
j |
|
k |
|
, тогда его действие на скалярную |
|
|
|
|
|
|
|||||||||
|
x |
|
y |
|
z |
|
dx |
|
|
y |
|
z |
|
|
функцию можно записать
φ |
φ |
|
φ |
|
φ |
, тогда φ 2φ |
2φ |
|
2 |
φ |
|
2 |
φ |
|
|||
dx |
i |
y |
j |
z |
k |
x2 |
y2 |
z |
2 |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
где i , j, k – орты декартовой системы координат. Оператор ставит в соответствие произвольной скалярной функции φ векторную функцию с проекциями на оси декар-
φ φ φ
товой системы координат x , y , z .
В развернутом виде в декартовой системе координат, учитывая, что
ξ2ξ 2ξ 2ξ , трехмерное волновое уравнение записывается следующим
x2 y2 z 2
образом:

|
2ξ |
|
2ξ |
|
2ξ |
|
1 2ξ |
. |
|
|||
|
x2 |
y2 |
z 2 |
V 2 |
t 2 |
|
||||||
|
|
|
|
|
|
|
|
|||||
Любая функция вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
ξ(r ,t) ξ(Vt |
r ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
является решением волнового уравнения, |
здесь |
|
|
|
||||||||
|
ξ(r ,t) ξ(x, y, z,t) , где |
r – радиус- |
||||||||||
вектор, которому можно сопоставить три декартовые координаты (x, y, z) . Таким об-
разом, любая периодическая функция, зависящая от времени |
t |
|
|||
и координат r , яв- |
|||||
|
и t |
|
|
|
|
ляется волной, если r |
связаны по закону r |
Vt . |
|
|
|
Если волна распространяется вдоль одного направления, тогда уравнение становится одномерным волновым уравнением. Одномерное волновое уравнение при рас-
пространении волны вдоль оси Ox имеет вид |
|
|
|||
|
|
|
|
|
|
|
2ξ |
|
1 |
2ξ |
. |
|
x2 |
V 2 |
t 2 |
||
|
|
|
|||
Являющиеся его решением функции вида ξ(Vt x) описывают плоские волны:
ξ(Vt x) – плоская бегущая волна, распространяющаяся в положительном направ-
лении оси x ;
ξ(Vt x) – плоская бегущая волна, распространяющаяся в отрицательном направ-
лении оси x .
|
Здесь t – время, x – координата, V – скорость распространения волны. |
|
||||||
|
Характеристики волн естественно связаны с характеристиками колебаний волны. |
|||||||
|
|
|
|
|
|
|
|
|
|
Безразмерный аргумент функции ξ(r Vt) , описывающей волновой процесс, |
|||||||
|
|
|
|
|
|
x |
|
|
называется |
ф а з о й в о л н ы . Фаза плоской волны ξ(Vt x) ξ |
ω t |
|
имеет |
||||
V |
||||||||
|
|
|
|
|
|
|
||
|
|
x |
|
|
|
|
||
вид |
ω t |
|
. Здесь ω – частота колебаний, называемая для волнового процесса |
|||||
|
||||||||
|
|
V |
|
|
|
|
||
ч а с т о т о й в о л н ы . |
|
|
|
|
||||
|
Скорость распространения колебаний, которую мы назвали скоростью волны, |
|||||||
является ф а з о в о й с к о р о с т ь ю в о л н ы . |
Она определяет скорость, с которой |
|||||||
перемещается поверхность постоянной (одинаковой) фазы волны. |
|
|
|
|||||
|
Минимальное расстояние между двумя точками, в которых фаза колебаний оди- |
|||||||
накова в один и тот же момент времени, называется д л и н о й в о л н ы |
λ . Волна |
|||||||
(плоскость постоянной фазы волны) проходит за один период колебаний T путь, равный длине волны λ . То есть,
λ VT .
Волна называется г а р м о н и ч е с к о й , если распространяющиеся колебания являются гармоническими.

График плоской волны |
|
График монохроматической |
|
|
плоской волны |
|
|
|
|
|
|
x
x
Для гармонических волн вводят понятие а м п л и т у д ы в о л н ы , |
которая равна |
амплитуде гармонических колебаний в данной точке пространства. |
|
И н т е н с и в н о с т ь ю в о л н ы называется количество энергии, |
переносимой |
волной в единицу времени через единичную площадку, перпендикулярную распростране-
нию волны. Для гармонических волн интенсивность пропорциональна квадрату амплитуды волны.
В о л н о в ы м |
ч и с л о м называют величину, равную отношению частоты ко- |
||||||
лебаний к фазовой скорости волны k |
ω |
|
2π |
|
2π |
. Тогда плоскую волну, являю- |
|
|
TV |
|
|||||
|
V |
|
λ |
||||
щуюся решением |
одномерного волнового |
уравнения, можно представить в виде |
|||||
ξ(ωt kx) . |
|
|
|
|
|
|
|
Если волновое уравнение трехмерное, то его решением может быть плоская вол- |
|||||||
|
|
|
|
|
|
||
на, которую можно записать в виде ξ(ωt kr ) , где k – в о л н о в о й в е к т о р , на-
правление которого совпадает с направлением распространения волны, а величина
|
|
|
|
2π |
|
|
|
|
|
||||
равна волновому числу |
k |
|
|
; |
r – радиус-вектор точки, в которой рассматриваем |
|
|
λ |
|||||
волну. |
|
|
|
|
||
|
|
|
|
|
||
Основные понятия физики волн мы определили, и далее мы будем рассматривать волновые процессы на примере э л е к т р о м а г н и т н ы х в о л н , частным случаем которых являются световые волны или свет.
Э л е к т р о м а г н и т н а я в о л н а – процесс распространения в пространстве возмущения электромагнитного поля.
Существование электромагнитных волн является следствием уравнений Максвелла. Для электромагнитного поля вдали от порождающих его свободных зарядов и мак-
ротоков эти уравнения имеют вид |
|
|
|
|
|
|
|
|
||
|
|
|
|
дB |
|
|
||||
Edl |
|
|
|
|
|
dS |
; |
DdS |
0 ; |
|
|
|
дt |
||||||||
(L) |
(S ) |
|
|
|
(S ) |
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
дD |
|
|
|||||||
Hdl |
|
|
|
|
|
dS |
; |
BdS |
0 . |
|
|
дt |
|||||||||
(L) |
(S ) |
|
|
|
(S ) |
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если среда однородна и изотропна, то |
D εε0 E |
и B |
μμ0 H. В этом случае |
||||||||||||||||||||||||||
уравнения Максвелла можно переписать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
μμ |
|
|
|
|
дH |
|
|
|
|
0 ; |
||||||||||||||||||
|
Edl |
0 |
|
|
|
дt |
dS |
; |
|
|
EdS |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(L) |
|
|
|
|
|
|
(S ) |
|
|
|
|
|
|
|
(S ) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
εε0 |
|
|
|
дD |
|
|
|
|
|
|
0 . |
|||||||||||||||||
|
Hdl |
|
|
|
дt |
dS ; |
|
|
|
HdS |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
(L) |
|
|
|
|
|
(S ) |
|
|
|
|
|
|
|
|
|
|
|
(S ) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если из этих уравнений вывести уравнения для векторов напряженностей E и |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H , то получим волновые уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
εμ |
2 |
|
|
|
|
|
|
|
εμ |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
E ε |
0 |
μ |
0 |
|
|
E |
и |
|
H ε |
0 |
μ |
0 |
|
H |
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
t |
2 |
|
|
|
|
|
|
|
t 2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Это значит, что напряженности |
|
|
E и |
H переменного электромагнитного поля в |
|||||||||||||||||||||||||
однородной, изотропной, непроводящей, нейтральной среде должны удовлетворять волновому уравнению, то есть переменное электромагнитное поле будет распространяться в пространстве в виде волны.
Сравнивая полученные уравнения с волновым уравнением, записанным в общем
виде, ξ |
1 |
2ξ |
, находим фазовую скорость электромагнитных волн |
|
V 2 |
t 2 |
|||
|
|
|
V |
|
|
1 |
1 |
|
|
или |
V |
|
c |
|
, где |
c |
|
|
1 |
|
|
3 108 |
м |
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
ε0μ0 |
|
|
|
εμ |
|
εμ |
|
0 0 |
с |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
В вакууме ε μ 1 |
и, соответственно, V c . |
Таким образом, величина |
|||||||||||||||||||||||||||||||||
c 3 108 |
м |
есть |
скорость распространения электромагнитных волн в вакууме. |
||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из уравнений Максвелла следует также, что в однородной и изотропной среде |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
k , E |
|
|
k |
|
|
μμ0 H |
, |
|
k , H k |
|
|
εε0 E |
, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εε0 |
|
|
|
|
|
|
|
|
|
μμ0 |
|
||||||||||
где квадратные скобки обозначают, как обычно, векторное произведение векторов.
Откуда видно, что электромагнитные волны в однородной изотропной среде пред- |
|||||
|
|
|
|
|
|
ставляют собой |
поперечные волны ( E k и |
H k ), кроме того, вектор напря- |
|||
|
|
|
|
|
|
женности электрического поля E перпендикулярен вектору напряженности маг- |
|||||
|
|
|
|
|
|
нитного поля Н , и оба поля колеблются в фазе. |
|
|
|||
|
|
|
|
|
|
Векторы E |
и Н вместе с волновым вектором k |
образуют правую тройку векто- |
|||
|
|
|
|
|
|
ров (E, H , k ) . То есть при вращении правого буравчика от первого вектора ко второму |
|||||
в сторону меньшего угла его поступательное движение будет направлено по третьему |
||
|
|
|
вектору. Циклические перестановки векторов H , k , E |
или k , E, H также будут обра- |
|
зовывать правую тройку.
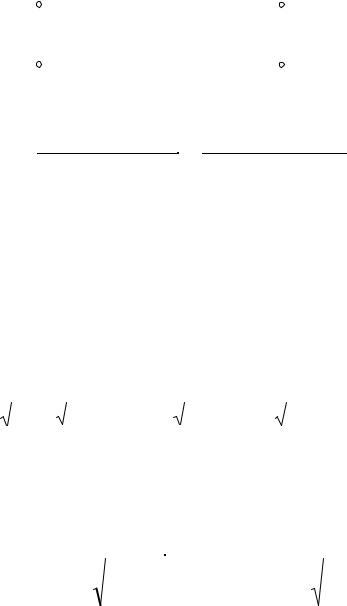
Если ось Ox выбрана по направлению распространения волны, то ось Oy можно выбрать так, что вектор напряженности электрического поля плоской монохроматической электромагнитной волны будет направлен по оси Oy Ey E0 cos(ωt kx φ),
тогда Ex Ez |
0 . Вектор напряженности магнитного поля этой волны будет иметь |
составляющие |
H z H0 cos( t kx ) и H x H y 0 . На рисунке представлен |
случай |
и x 0 при t 0, тогда Ey E0 sin( ωt kx) и H z H0 sin(ωt kx) . |
2 |
|
y
E
V
x
z B
Электромагнитные волны, как любые волны, не переносят вещество – это распространяющиеся электрические и магнитные поля, они переносят электромагнитную энергию. Для характеристики переноса энергии используют векторное произведение напряженностей электрического и магнитного поля – в е к т о р П о й н т и н г а (J. Poynting, 1852–1941), введенный Джоном Пойнтингом в 1884 году
|
|
|
S |
E, H |
. |
Вектор S является вектором плотности потока электромагнитной энергии. Он по-
казывает, в каком направлении и какое количество энергии переносится за единицу времени через единичную площадку, расположенную перпендикулярно распространению волн.
По определению интенсивности волны она равна среднему значению модуля вектора Пойнтинга, при этом усреднение должно проводиться или за целое число периодов или за время, много большее периода колебаний,
|
|
|
|
|
|
|
|
|
|
|
|
|
I S |
εε0 E 2 |
μμ0 H 2 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μμ0 |
εε0 |
|
|||||
|
|
|
|
|
||||||||
Электромагнитные волны кроме энергии переносят импульс, и поскольку волны поглощаются и отражаются, они передают импульс поглощающей или отражающей поверхности, то есть оказывают на нее давление. Полученное Дж. Максвеллом в 1873 году выражение для давления плоской монохроматической электромагнитной волны при нормальном падении на поверхность с коэффициентом отражения R
P 12 εε0 E 2 (1 R)

было экспериментально доказано в 1900 году П. Н. Лебедевым (1866–1912). Из-за малости величины давления, например, давление света Солнца на поверхность Земли составляет P 5 мкПа, измерение давления потребовало изобретательности и мастерства.
При падении плоской волны на поверхность под углом давление, оказываемое волной на поверхность, описывается выражением
P 12 0 E 2 (1 R)cos2 .
То, что свет ведет себя подобно волне, было установлено за много лет до Максвелла. Но никто не мог сказать, что это за волна, то есть распространением каких именно колебаний является свет. Максвелл, основываясь на своей теории, утверждал, что свет – это электромагнитная волна.
Эта точка зрения постепенно получила признание, хотя большинство ученых поначалу считали волны, получающиеся из уравнений Максвелла, абстрактными волнами, не имеющими физического смысла. Окончательно точка зрения Максвелла получила признание лишь после того, как в 1887 году Генриху Герцу (H. Hertz, 1857–1894) впервые удалось генерировать и наблюдать электромагнитные волны на опыте.
В качестве источника электромагнитных волн был использован колебательный контур. Герц, уменьшая число витков катушки индуктивности, а также разворачивая пластины конденсатора, чтобы они лежали в одной плоскости, перешел от закрытого колебательного контура, переменное электрическое поле в котором сосредоточено между пластинами конденсатора, а магнитное – внутри катушки индуктивности, к от-
крытому колебательному контуру – в и б р а т о р у Г е р ц а , переменное поле кото-
рого заполняет окружающее его пространство.
Имея широкий диапазон частот ν 2ωπ (или длин волн λ VT Vν ), электро-
магнитные волны отличаются друг от друга по способам создания и регистрации, а также по своим свойствам. Электромагнитные волны условно делят на несколько групп:
|
|
|
λ , м |
|
|
ν , Гц |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Радиоволны |
|
|
10 |
3 |
10 |
4 |
3 10 |
5 |
12 |
|||
|
|
|
|
|
|
3 10 |
||||||
Световые волны |
5 10 |
4 |
10 |
9 |
11 |
17 |
||||||
|
|
|
|
6 10 |
|
3 10 |
||||||
инфракрасное |
5 10 4 |
7,5 10 7 |
6 1011 |
4 1014 |
||||||||
излучение |
|
|
|
|
|
|
|
|
|
|
|
|
видимый свет |
7,5 10 7 |
4 10 7 |
4 1014 7,5 1014 |
|||||||||
ультрафиолетовое излучение |
4 10 7 |
10 9 |
7.5 1014 |
3 1017 |
||||||||
Рентгеновское |
2 10 |
9 |
6 |
10 |
12 |
17 |
19 |
|||||
излучение |
|
|
|
|
1.5 10 |
|
5 10 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
-излучение |
меньше 6 10 12 |
больше 5 1019 |
||||||||||
О п т и ч е с к и м и з л у ч е н и е м или с в е т о м называются электромагнитные
волны, длины волн которых лежат в диапазоне 10 9 5 10 4 м . Свет включает в се-
бя инфракрасное излучение, видимый свет, ультрафиолетовое излучение.

Границы между диапазонами волн условны и в разных справочниках слегка отличаются. Для видимого диапазона удобнее запоминать интервал длин волн
(0,4 0,75) 10 6 м и интервал частот (0,4 0,75) 1015 Гц , так как в этом случае
они имеют похожий вид. Следует помнить то, что длина волны 0,4 10 6 м соответствует частоте 0,75 1015 Гц , а 0,75 10 6 м – частоте 0,4 1015 Гц .
В произвольной среде скорость света не превосходит скорости света в вакууме
|
|
с |
ε 1, μ 1. Это выражение можно записать так |
||||||||||||
V |
|
|
|
с , так как |
|||||||||||
|
|
|
|||||||||||||
|
εμ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
, где |
n |
|
εμ |
. |
|
||
|
|
|
|
|
n |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Введенная новая |
величина n называется |
о п т и ч е с к о й |
п л о т н о с т ь ю |
|||||||||||
с р е д ы или абсолютным показателем преломления среды . |
Он показывает, |
||||||||||||||
во сколько раз скорость света в среде меньше скорости света в вакууме n Vc . Или,
другими словами, во сколько раз длина волны света в среде λ меньше длины волны света в вакууме λ0
λ VT nc T cTn λn0 .
Для немагнитных сред (например, вода, стекло и многие другие прозрачные среды) μ 1 и, следовательно, n 
 ε .
ε .
Интерференция волн
И н т е р ф е р е н ц и е й |
в о л н называется взаимодействие конечного числа волн, |
при котором происходит |
устойчивое во времени их усиление в одних точках про- |
странства и ослабление в других точках. Интерферировать могут только когерентные волны. Волны называются к о г е р е н т н ы м и (от лат. cohaerentia – связь), если раз-
ность фаз между колебаниями волн в одной точке пространства постоянна.
И н т е р ф е р е н ц и е й с в е т о в ы х в о л н называется устойчивое перераспре-
деление светового потока при взаимодействии конечного числа (двух и более) когерентных волн.
Если на пути света установить непрозрачный экран, то в результате перераспределения светового потока на экране возникает и н т е р ф е р е н ц и о н н а я к а р т и н а ,
состоящая из чередующих более светлых и более темных областей. Для возникнове-
ния интерференционной картины световые волны должны быть когерентными. В классических экспериментах по интерференции когерентные волны получают от одного
источника, для чего один световой луч разделяют на несколько лучей.
Описывая свет, обычно говорят о векторе Е , который называют световым вектором. Это связано с тем, что действие света обычно обусловлено действием именно
электрического поля. Мы, рассматривая свет, также будем говорить о напряженности |
|||||
|
|
|
|
|
|
электрического поля Е . |
|
|
|||
Рассмотрим классические опыты по интерференции. |
|||||
|
|
|
|
Э |
1. Опыт Юнга (1801 г.) |
|
|
|
|
||
|
S1 |
|
|
||
|
|
|
В эксперименте источником света служит ярко |
||
S |
|
|
|
||
|
|
|
|||
|
|
И |
освещенная щель S , световая волна от которой прохо- |
||
|
|
|
|
||
|
|
|
|
дит две равноудаленные щели S1 и S2 , параллельные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
щели S . Интерференционная картина наблюдается на |
|
|
|
|
|
|
экране Э (область И ) . |

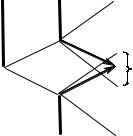
2.Зеркала Френеля (1816 г.)
Для опыта использовались два зеркала, расположенные под углом друг к другу, близким к 1800, и источник света S , который отражается в обоих зеркалах. Световые лучи, отразившиеся от зеркал, можно считать вышедшими из мнимых источников S1 и S2 ,
являющихся мнимыми изображениями S в зеркалах. Мнимые источники когерентны, и исходящие из них пучки света интерферируют в области перекрытия. Интерференционная картина наблюдается на экране Э в области И , закрытой защитным экраном З от прямого попадания света.
2. Бипризма Френеля
Для получения интерференции использовалась бипризма, состоящая из двух сложенных основаниями одинаковых призм с малыми преломляющими углами. Свет от источника S преломляется в обеих призмах. Преломленные лучи можно считать исходящими из мнимых источников S1 и S2 , яв-
ляющихся когерентными. На экране Э в области И наблюдается интерференционная картина.
З Э
S 
И
S1
S2
Э
S1
И
S
S2
3. Билинза Бийе |
|
|
|
|
В опыте использовалась собирающая |
|
Э |
||
линза, разрезанная пополам, с раздвинутыми |
|
S1 |
||
половинами. На полученную билинзу направ- |
|
|||
|
|
|||
ляют свет от щели |
S , параллельной плоско- |
|
|
|
сти разреза. В S1 и |
S2 получаются действи- |
S |
И |
|
тельные изображения щели. Пучки света, |
||||
|
|
|||
проходящие через S1 и S2 , когерентны, и на |
|
S2 |
||
экране в области перекрытия и будет наблю- |
|
|||
даться интерференционная картина. |
|
|
||
Независимо от способа получения интерференционной картины в любом случае необходимы когерентные источники, испускающие когерентные волны. Опыты по интерференции отличаются используемыми приспособлениями для создания этих источников, например, устройствами для отражений и преломлений, обеспечивающих наложение одной световой волны на другую.
Рассмотрим наложение волн более подробно. Будем рассматривать колебания одного направления и ограничим наше рассмотрение только наложением двух лучей
