
Курс лекций по физике - Часть_2 - Электрическое_и_магнитное_поле_Оптика
.pdf
|
|
|
|
|
|
|
|
|
|
Q |
q |
|
|
|
1 |
|
Q |
|
|
|
|
Q 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
W |
A dq |
dq |
|
qdq |
или окончательно |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
C |
|
|
C |
0 |
|
|
|
|
2C |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
W |
Q 2 |
|
C2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2C |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Если рассмотреть плоский конденсатор с расстояниями между пластинами |
|||||||||||||||||||||||||||||||
площадью пластин S , подставить C |
0 S |
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
Q |
|||||||||||||||||
|
|
и учесть, что |
|
|
, то |
||||||||||||||||||||||||||||
|
d |
0 |
0 S |
||||||||||||||||||||||||||||||
|
2 |
|
2 |
2 |
2 |
|
2 |
|
|
|
2 02 S 2 E |
2d |
|
1 |
|
|
|
|
2 |
|
|
1 |
|
2 |
|
||||||||
Q |
|
|
|
0 S |
|
E |
|
, то получим W |
|
|
|
|
|
|
|
|
|
|
|
0 E |
|
Sd |
|
|
0 E V . Здесь |
||||||||
|
|
|
|
|
|
|
2 0 S |
|
|
2 |
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
d и
есть
V –
объем пространства между пластинами конденсатора, где локализовано электрическое поле. Тогда выражение
12 0 E 2 WV w
имеет смысл объемной плотности энергии электрического поля.
Полученное здесь выражение объемной плотности энергии электрического поля справедливо в общем случае электрического поля напряженностью E .
Пластины конденсатора имеют разноименный заряд, следовательно, они притягиваются друг к другу. Пластины реального конденсатора находятся на фиксированном расстоянии, поскольку сила притяжения компенсирована внешними силами.
Найдем силу притяжения между пластинами – силу притяжения, с которой на одну пластину конденсатора действует другая пластина. Заряд на одной пластине Q ,
тогда сила притяжения должна быть равна F QE SE , где E – напряженность электрического поля, в котором находится пластина. Это поле E создает одна вторая
пластина, и оно имеет напряженность E |
|
. Следовательно, сила равна |
|
||
2 0 |
F 2 S . 2 0
Выражая плотность заряда 0 E через напряженность поля внутри конден-
сатора, создаваемого обеими пластинами E 2E |
|
, получим |
|
||
|
0 |
|
F 12 0 E 2 S .
Если между пластинами конденсатора помещен диэлектрик, тогда он будет испы-
тывать давление
P FS 12 0 E 2 w .

Электрический ток
В предыдущей теме мы рассмотрели взаимодействие и свойства систем неподвижных зарядов. Перед тем как перейти к взаимодействию движущихся зарядов, нужно научиться описывать их движение, чему посвящена данная тема.
Э л е к т р и ч е с к и м т о к о м называется упорядоченное движение зарядов. Ток характеризуется направлением тока и силой тока .
Н а п р а в л е н и е т о к а совпадает с направлением движения положительных зарядов.
С и л а т о к а равна величине заряда, прошедшего в единицу времени через поперечное сечение проводника
|
|
|
|
|
|
|
I |
dQ |
|
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
I |
|
|
|
|||||
Электрический ток называется |
п о с т о я н н ы м э л е к т р и ч е с к и м т о к о м , |
||||||||||||||||||||
если сила тока не изменяется со временем. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Для постоянного тока ( |
) |
|
I |
Q |
|
, и в этом случае заряд, |
прошедший |
||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|||||
по проводнику за время , будет равен |
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||
Для более детального описания протекания заряда по проводнику вводят п л о т - |
|||||||||||||||||||||
н о с т ь |
|
т о к а |
, равную величине заряда, |
прошедшего через единицу площади по- |
|||||||||||||||||
верхности, перпендикулярной направлению тока, |
|
|
|
||||||||||||||||||
|
|
|
|
I const |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
j |
dI |
|
qnv |
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
t |
|
Q dSIt |
|
|
|
|
|
|
|
|
|
|
|||||
Здесь |
|
– сила тока, прошедшего через |
, |
|
|
|
– заряд одного носителя заряда, |
|
– |
||||||||||||
концентрация и |
j – средняя скорость упорядоченного движения носителей заряда. |
|
|
||||||||||||||||||
Если плотность тока одинакова во всех точках сечения проводника ( |
|
|
), |
||||||||||||||||||
то j |
|
I |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если ввести вектор, по величине равный плотности тока и направленный по дви- |
|||||||||||||||||||||
dI |
|
|
|
dS |
q |
|
n |
|
|||||||||||||
жению положительных зарядов, то мы получим в е к т о р п л о т н о с т и т о к а |
|
|
|||||||||||||||||||
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
j const |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
j |
qnv |
. |
|
|||||||||||
Скорость упорядоченного движения зарядов пропорциональна напряженности электрического поля, которое вызывает их движение

vE .
Коэффициент пропорциональности называется подвижностью носителя за-
|
|
|
|
|
. Величина называется удельной проводимостью ме- |
|
|
||||
ряда. Тогда |
j |
qn E E |
|
||
|
|
|
|
|
|
талла.
Мы знаем, что электростатические поля могут только вызывать перераспределение зарядов в проводнике, которое сопровождается выравниванием потенциала, при котором движение зарядов прекращается. Для постоянного движения зарядов в проводнике требуются силы не электростатической природы.
Силы, поддерживающие постоянную разность потенциалов и обеспечивающие протекание тока, называются с т о р о н н и м и с и л а м и . Под действием сторонних сил электрические заряды движутся внутри источника против сил электростатического поля, вследствие чего на клеммах источника поддерживается постоянная разность потенциалов, и при подключении к источнику электрической цепи в ней потечет электрический ток.
Природа сторонних сил может быть различной. В гальванических элементах они возникают за счет энергии химических реакций, в генераторе – за счет механической
энергии вращения ротора генератора и т. п.
F стор можно ввести напряженность поля сторонних сил
|
|
|
|
|
|
|
F |
||
E |
|
|
стор |
. Результирующее поле в проводнике будет суммой электростатическо- |
стор |
|
|||
|
|
q |
||
|
|
|
||
|
|
|
|
го поля E и поля сторонних сил Eстор |
|
|
|
|
|
||
|
E E Eстор . |
||
Работа сторонних сил по перемещению единичного положительного заряда на участке цепи (1-2) называется э л е к т р о д в и ж у щ е й с и л о й (ЭДС), действующей
на этом участке, и обозначается ε12
(2)
ε12 Aстор (един) Eстор dl ,
(1)
где dl – вектор, направленный по току, длина которого равна длине бесконечно малого участка цепи.
Если участок электрической цепи содержит источник ЭДС, этот участок назы-
вается н е о д н о р о д н ы м у ч а с т к о м ц е п и . Для неоднородного участка цепи
полная работа электростатических и сторонних сил по перемещению единичного положительного заряда, называемая н а п р я ж е н и е м , равна
(2) |
|
|
|
(2) |
|
(2) |
|
U A12(един) |
|
|
Eстор dl |
Edl ε 1 2 |
|||
E dl |
|||||||
(1) |
|
|
|
(1) |
|
(1) |
|
или, окончательно, U ε 1 2 .

Для однородного участка цепи (не содержащего источник ЭДС) напряжение определяется выражением
U 1 2 .
Для замкнутой цепи 1 2 , поскольку работа электростатических сил в замк-
нутом контуре равна нулю, и напряжение равно ЭДС U ε, то есть полная работа по перемещению заряда в замкнутой цепи равна работе сторонних сил.
Сила тока на однородном участке цепи связана с приложенным напряжением з а к о н о м О м а , установленным в 1887 году Г. Омом (G. Ohm, 1787–1854): если под действием сторонних сил на однородном участке проводника создается напряжение U , то на данном участке проводника протекает ток силой I , которая пропорциональна приложенному напряжению
|
|
|
I |
1 |
|
|
|
|
|
|
|
|
|
|
|
U |
или, |
как часто записывают, |
IR U |
. |
|||||
|
||||||||||||
|
|
|
|
R |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
Величина R , входящая в закон Ома, называется электрическим сопротивлени- |
|||||||||||
ем участка проводника. |
|
j |
I |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
S |
|||||
|
|
|
|
|
|
|
|
|||||
|
Если к однородному участку проводника длины L и поперечного сечения S при- |
|||||||||||
ложить напряжение U , оно создаст в проводнике однородное электрическое поле |
||||||||||||
E |
U |
, так как для однородного поля U EL. Это поле обеспечивает проте- |
||||||||||
|
||||||||||||
|
L |
|
|
|
|
|
|
|||||
кание тока с постоянной плотностью |
|
|
. Подставив плотность тока и напряжен- |
|||||||||
ность в выражение j σE , которое является законом Ома в дифференциальной форме, получим
I |
σ |
U |
или |
I σ |
S |
U . |
|
|
|
||||
S |
|
L |
|
|
L |
|
Коэффициент пропорциональности (величина обратная сопротивлению) называется
п р о в о д и м о с т ь ю |
1 |
σ |
S |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
R |
|
L |
|
|
|
|
|
|||||||
Мы получили, что сопротивление R зависит от природных свойств проводника и |
|||||||||||||||
от геометрических размеров участка проводника |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
1 |
|
L |
ρ |
L |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
σ S |
S |
|
|
|
|||||
Величина, обратная удельной проводимости |
ρ |
1 |
, называется у д е л ь н ы м |
||||||||||||
σ |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
с о п р о т и в л е н и е м , которое, как и удельная проводимость, зависит только от природы проводника и не зависит от его формы и размеров. По определению удельное со-
противление материала проводника есть сопротивление участка проводника единичной длины и единичной площади поперечного сечения.

|
|
|
0 |
|
C |
|
t |
Для металлов удельное сопротивление растет с температурой. Этому не стоит удивляться, так как с ростом температуры атомы металла движутся быстрее и больше мешают упорядоченному движению электронов. В широких диапазонах температуры сопротивление увеличивается практически линейно
0 1 t .
Коэффициент называется температурным коэффициентом сопротивления.
Для разных металлов температурный коэффициент свой, причем значения зависят от диапазонов температуры, поэтому при использовании табличных значений следует обращать внимание на интервал температур, для которого справедливо используемое значение.
При низких температурах наблюдается отклонение от линейного закона. Для
большинства реальных металлов характерно наличие остаточного сопротивления ост |
||||||
|
|
|
при абсолютном нуле. Это связано с наличием |
|||
|
|
|
примеси (чужеродных атомов) в кристаллической |
|||
|
|
|
решетке металла и ее неидеальностью (наличием |
|||
|
|
|
дефектов кристаллической структуры). |
|
||
|
|
|
В |
то же |
время некоторые |
металлы |
|
|
( Al, Pb, Zn , их сплавы и другие) проявляют |
||||
|
|
|
||||
ост |
|
T |
вблизи абсолютного нуля при температурах, раз- |
|||
|
ных для |
каждого |
вещества (T 0,14 |
20 K ), |
||
|
|
|
||||
свойство с в е р х п р о в о д и м о с т и – их сопротивление становится равным нулю.
Сверхпроводимость является макроскопическим квантовым эффектом и объясняется на основе квантовой механики. Физическая модель сверхпроводимости была создана в
1957 году.
Для неоднородного участка цепи з а к о н О м а принимает вид
I ε 1 2 .
R
Мы можем записать обобщенный закон Ома в виде
I R1 U ,
где U ε 1 2 для неоднородного участка, U 1 2 – для однородного участка.
|
|
|
|
|
|
|
|
|
|
Рассмотрим замкнутую цепь, содержащую ис- |
|
a ε |
|
|
|
|
r |
|
|
точник ЭДС с внутренним сопротивлением r |
и под- |
||
|
|
|
|
|
|
||||||
|
|
|
|
b ключенную к источнику нагрузку сопротивлением R . |
|||||||
|
|
|
|
|
|
||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
Запишем закон Ома для неоднородного участка |
|
|
|
|
|
|
|
|
|
|
|
цепи ab (внутри пунктира) |
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
I ε a b , |
|
|||||
|
|
|
|
R |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
откуда Ir ε a b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Запишем закон Ома для однородного участка цепи ba (снаружи пунктира)
I b a ,
R
откуда найдем IR b a . Тогда Ir IR ε.
И мы получаем з а к о н О м а д л я з а м к н у т о й ц е п и
|
|
|
|
|
|
|
|
||
|
I |
ε |
. |
|
|
|
|
||
|
r R |
|
|
|
εR |
|
|||
Напряжение на клеммах источника будет равно U |
ab |
IR |
. |
||||||
|
|||||||||
|
|
|
|
|
|
r R |
|||
|
|
|
|
|
|
|
|||
При протекании тока (движении заряда) совершается работа. Для этого требуется энергия, поступление которой обеспечивается источником ЭДС.
Энергия, необходимая для переноса заряда dq Idt между точками, напряжение
между которыми U , равна
dW Udq IUdt .
Мощность, потребляемая от источника ЭДС, |
P |
dW |
IU |
. |
|
|
||||
dt |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Если проводник неподвижен, вся энергия идет на нагревание проводника. Тогда с |
||||||||||
учетом закона Ома |
|
|
|
|
|
|
|
|
|
|
t |
t |
t |
|
|
t |
2 |
|
|
||
Q W dW Pdt IUdt I 2 (t)Rdt |
U |
|
|
(t) |
dt . |
|||||
|
|
|
|
|||||||
0 |
0 |
0 |
|
|
0 |
|
R |
|||
|
|
|
|
|
|
|
||||
Если ток постоянен ( I = const , U = const ), то выделяемое тепло определяется выражением
Q I 2 Rt U 2 t .
R
В этом случае тепловая мощность равна
P I 2 R U 2 .
R
Полученные выражения, описывающие тепловое действие электрического тока,
носят название з а к о н а Д ж о у л я – Л е н ц а (J. Joule, 1818–1889, Э. Ленц, 1804– 1865).
Если проводник перемещается, то часть энергии будет израсходована на совершение работы
A Pdt Q .
При постоянном токе работа будет равна A IUt I 2 Rt .
При расчете электрических цепей, содержащих разветвленные неоднородные участки, использование закона Ома часто неудобно, так как расчет становится громоздким

и сложным. В этих случаях применяют определенные правила расчета – п р а в и л а К и р х г о ф а (G. Kirchhoff, 1824–1887), являющиеся следствием фундаментальных законов физики.
1. П е р в о е п р а в и л о Кирхгофа – правило узлов.
Суммарная сила входящих в узел токов равна суммарной силе выходящих токов.
Iвход Iвыход
или, если считать, как это принято, втекающие токи положительными, а вытекающие
– отрицательными, то полная сумма всех токов равна нулю
Ii 0 .
Узлом называется точка электрической цепи, в которой соединены более двух проводников.
Первое правило Кирхгофа является следствием закона сохранения заряда – сколько заряда втекает ежесекундно в узел, столько должно и вытекать – заряд не может исчезнуть.
2.В т о р о е п р а в и л о Кирхгофа – правило контуров.
Взамкнутом контуре сумма ЭДС равна сумме падений напряжения на однородных участках
n |
m |
|
εi Ik Rk |
. |
|
i 1 |
k 1 |
|
Второе правило Кирхгофа является следствием потенциальности электростатического поля – работа сил электростатического поля A при перемещении заряда по замкнутому контуру равна нулю. Эта работа может быть найдена на всех участках цепи, как разность полной работы электростатических и сторонних сил A и работы сторонних сил Aстор . Тогда
|
|
|
|
|
|
A Aстор 0 . |
|
||
Если перемещаемый заряд единичный и положительный, то поскольку по опреде- |
||||
лению A(един) k U k – падение напряжения на k -м участке цепи, а Aстор (един) i |
εi – |
|||
ЭДС на k -м участке цепи, получим |
|
|
|
|
|
|
|
|
|
|
n |
m |
|
|
|
εi |
U k |
. |
|
|
i 1 |
k 1 |
|
|
Пользуясь обобщенным законом Ома, |
можем записать U k I k Rk . Тогда второе |
|||
правило Кирхгофа примет вид |
|
|
|
|
|
n |
m |
|
|
εi I k Rk . |
|
|||
i 1 |
k 1 |
|
||
В правой части суммирование ведется по всем участкам цепи, содержащим сопротивление, в левой – по всем участкам, содержащим ЭДС.
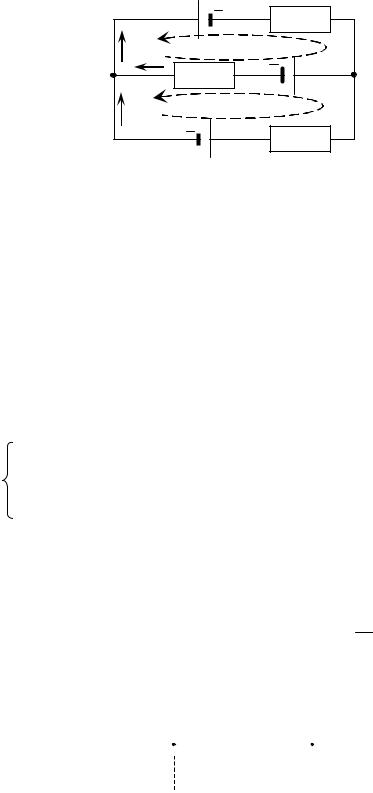
Как пример использования правил Кирхгофа рассмотрим цепь, изображенную на рисунке.
Применим первое правило. Выберем направление протекания токов, как показано на рисунке. В данной схеме два узла a и b . Первое правило, в записи для этих узлов, будет отличаться только знаками токов (левая и правая части поменяются местами)
I1 I2 I3 .
|
|
|
ε1 |
|
|
|
|
|
I1 I |
2 |
R2 |
a |
|
|
|
|
|
|
|
|
I3 |
ε3 |
|
|
|
R1 |
|
|
|
b |
|
ε2 |
||
R3 |
||
|
При использовании второго правила выберем направление обхода замкнутых контуров, как указано пунктиром.
Тогда при суммировании ЭДС по определению нужно брать ЭДС с плюсом, если при обходе контура первым будет отрицательная клемма (минусовой полюс) источника, а затем положительная клемма (плюсовой полюс), в этом случае ЭДС создает ток, направленный в сторону обхода контура. Если полюса будут встречаться при обходе контура в обратном порядке, то ЭДС нужно брать с минусом, в этом случае ЭДС создает ток, направленный в сторону против обхода контура.
При суммировании падений напряжения на резисторах ток будем брать с плюсом,
если его направление совпадает с направлением обхода, и с минусом – в противном
случае. Тогда для нашей схемы получим
ε1 ε2 I1R1 I2 R2 ,
ε2 ε3 I2 R2 I3R3 .
Или оба правила вместе
ε1 ε2 I1R1 I2 R2 ,
ε2 ε3 I2 R2 I3R3 ,
I1 I2 I3 .
Если полученная при решении уравнений сила тока в какой-либо ветви цепи получится отрицательной, то это означает, что в данной ветви ток будет протекать в направлении, противоположном выбранному.
Для простых цепей вместо правил Кирх-
гофа можно использовать правила нахождения |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
эквивалентного сопротивления при последо- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
R |
R2 |
|
|
|
|
Rn |
|||||||||||
вательном соединении резисторов |
|
|
|
|
|
|
|||||||||||||
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R Ri |
|
|
|
|
|
R1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и при параллельном соединении резисторов |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
R2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
i 1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которые могут быть получены из закона Ома |
|
|
|
|
Rn |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
или правил Кирхгофа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Электромагнетизм
В 1820 г. датский физик Ханс Эрстед (H. Ørsted, 1777–1851) показывал студентам тепловое действие тока. При включении тока отклонилась стрелка случайно оказавшегося рядом компаса. Описание этого опыта вызвало лавину новых открытий. Так родилась новая область физики – электродинамика.
Частью электродинамики (электромагнетизма) является м а г н и т о с т а т и к а ,
изучающая не изменяющиеся во времени (стационарные, или постоянные) магнитные поля, с которых мы начнем наше рассмотрение.
М а г н и т н о е п о л е – силовое поле (подобное гравитационному или электриче-
скому), окружающее токи и постоянные магниты. Магнитное поле не действует на неподвижные заряды, оно может создаваться только движущимися зарядами и действует только на движущиеся заряды.
Магнитные силы, действующие со стороны магнитного поля на движущиеся заряды, могут:
–искривлять их траекторию (если заряд движется в свободном пространстве);
–отклонять проводник (если заряды движутся в проводнике);
–поворачивать контур (если проводник образует замкнутый контур).
Все объекты, на которые действует магнитное поле:
движущиеся заряды,
проводники с током,
контуры с током,
постоянные магниты,
являются источникамитакжемагнитного поля.
изменяющееся электрическое поле,
Последний источник мы упоминаем пока лишь для полноты картины, говорить о нем будем в самом конце темы, когда будет идти речь об электромагнитной индукции. Пока рассмотрим только первые четыре источника.
Для описания магнитного поля нужно ввести его характеристики. Естественно это сделать так же, как, например, в электричестве, по силовому действию поля. Сделать это можно несколькими способами. В качестве объекта, на который действует сила со стороны магнитного поля, можно выбрать любой из объектов или движущийся заряд, или проводник с током, или контур с током, или магнит. Принципиальной разницы нет. Обычно используют какой-нибудь из первых двух способов. Мы рассмотрим оба и покажем их равнозначность.
Воспользуемся сначала первым способом – рассмотрим движущийся заряд.
На заряд, движущийся в магнитном поле, будет действовать сила, которую будем на-
зывать магнитной силой FM . Экспериментально установлено:
вектор силы перпендикулярен вектору скорости ( FM V );
если изменить направление скорости заряда, то сила изменит свое направление, но при этом останется перпендикулярной некоторому направлению, совпадающему с направлением магнитной стрелки, помещенной в точку, где находится заряд;
если изменить величину заряда, то сила по величине пропорциональна величине заряда q ( FM ~ q );

если изменить модуль скорости, то величина силы пропорциональна скорости его движения V ( FM ~ V ).
При изменении условий опыта, |
измеряя величину силы, действующей на заряд q , |
|||
можно убедиться, что отношение |
|
FM |
не зависит от величин q , V и угла меж- |
|
Vqsin α |
||||
|
|
|||
ду направлениями скорости и магнитной стрелки и принимает определенные значения в каждой точке пространства.
Исходя из этого, для описания магнитного поля введем некоторый вектор, назы- |
|
|
|
ваемый в е к т о р о м м а г н и т н о й и н д у к ц и и B |
, который является силовой ха- |
|
|
рактеристикой магнитного поля. Направлением вектора B выбирается направление |
|
|
|
магнитной стрелки (которому перпендикулярна сила |
FM , действующая на движу- |
щийся заряд) в ту сторону, куда направлен ее северный конец. Величину магнитной индукции в данной точке пространства определим так:
B FM . qV sin α
|
|
|
|
|
|
|
|
|
|
|
|
Учтем, что FM B и, кроме того, FM V , то, следовательно, |
FM V , B , |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
где |
V , B – |
векторное |
произведение векторов V |
и |
B , |
и |
его модуль |
||||
|
|
|
|
VB sin . |
|
|
|
|
|
|
|
|
V , B |
|
|
|
|
|
|
|
|||
|
|
Суммируя все перечисленное, можно записать |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FМ |
kqV , B , |
|
|
|
|
где k – коэффициент пропорциональности. |
|
|
|
|
|||||||
|
|
Поскольку индукция магнитного поля является новой физической величиной, и |
|||||||||
для нее нет единицы измерения, то выберем единицу измерения индукции магнитного поля так, чтобы коэффициент пропорциональности был равным единице k 1.
Тогда, используя введенную характеристику магнитного поля – индукцию маг- |
|||
|
|
|
|
нитного поля B , для силы, действующей на заряд q , движущийся со скоростью V |
|||
в магнитном поле, получим выражение |
|
|
|
|
|
|
|
|
|
|
|
|
FM q V , B |
. |
|
Эту силу, называют м а г н и т н о й |
с и л о й Л о р е н ц а (H. Lorentz, 1853–1928), |
||
или иногда ее называют магнитной составляющей силы Лоренца. В последнем слу-
|
|
|
чае с и л о й Л о р е н ц а называют силу F |
qE q V , B , действующую на движу- |
|
щийся заряд в электрическом и магнитном полях.
По определению векторного произве-
дения – |
модуль |
магнитной силы |
|
FM qVBsin α , где α – угол между век- |
|
||
|
|
|
|
торами V и |
B . Направлена магнитная сила |
B |
|
перпендикулярно к плоскости, в которой |
|
||
|
|
|
|
лежат векторы V и |
B . Заметим, что если |
|
|
FM
+ |
V |
V |
|
|
B FM
