8. Бортовая качка судна на регулярном волнении с заданной диаграммой остойчивости

Используем полученные энергетические соотношения для нелинейного уравнения бортовой качки , имеющего вид :

(78)

Разделив на J₁=(J_хх+λ₄₄), получим

, (79)

где ,w()=,m()=.

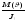Решение уравнения (78) будем искать в виде .

Тогда угловая скорость будет

.

Используем энергетические зависимости (76) и (77). Получим

=;

=, (80)

где

=.

. (81)

Подставляя (81) в (80), получим:

=;

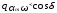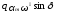=. (82)

Введем следующие обозначения: зависимость

(83)

будет называться средней частотой на наклонении судна от 0 до , а зависимость

(84)

средним сопротивлением при наклонении от 0 до .

Тогда вместо уравнений (82) получим:

, (85)

(86)

Возводя в квадрат каждое из этих уравнений и сложив, получим общее выражение для амплитуды бортовой качки:

(87)

Разделив (86) на (85), получим общее выражение для фазового угла

(88)

Формула (87) для амплитуды выражает зависимость амплитуды от частоты в неявном виде, так как в правую часть входят и, которые сами являются функциями амплитуды. Поэтому вычислить амплитуду по этой формуле невозможно. Рассмотрим случай, когда сопротивление линейное, а восстанавливающий момент задан диаграммой статистической остойчивости.

Линейное сопротивление можно представить выражением

W()=(89)

Найдем среднее сопротивление:

(90)

Подставив (90) в выражения для амплитуды и фазы (87) и (88), получим

; (91)

(92)

Так как формула (91) выражает зависимость между иω в неявном виде, решим данное уравнение относительно ω. Возведем в квадрат обе части этого уравнения:

;

. (93)

Преобразуем (93) в биквадратное уравнение относительно частоты ω.

(94)

Решая уравнение (94) сначала относительно , получим

(95)

Задаваясь различными значениями необходимо вычислить по формуле (83) с использованием заданной диаграммами остойчивости. Затем производим вычисления по формуле (95) и получаем зависимость ω() или . Из-за наличия двойного знака перед квадратным корнем получаем два значения частотыω₁ и ω₂, соответствующие заданному значению амплитуды .

Кривая будет иметь максимум при равенстве нулю величины, стоящей под знаком радикала .Полагая, радикал равным нулю получим:

(96)

С другой стороны равенство нулю радикала дает зависимость:

(97)

Совместное решение системы уравнений (96) и (97) дает точку, соответствующую максимуму кривой .

Из формулы (97) имеем:

=(98)

Подставим (98) в уравнение (96):

Откуда :

. (99)

Из раздела линейной качки известно, что отношение мало по сравнению с единицей.

Это положение можно распространить и на нелинейную качку. Тогда получим:

или

. (100)

Из уравнения (97) получим выражение для максимальной амплитуды, решая его относительно :

(101)

Пренебрегая вторым слагаемым под знаком радикала, получим

(102)

По формуле (102) вычислить максимальное значение невозможно, так каквходит в правую часть в неявном виде. Эту проблему можно решить графическим способом. Перепишем формулу (102) следующим образом:

.

Но, согласно (101) , значит

. (103)

Таким образом, является линейной функцией при угловом коэффициенте

. (104)

Зависимость (103) на графике изобразится наклонной прямой, проходящей через начало координат под углом β и вертикальной оси.

Таким образом, точка максимума амплитудной кривой, с одной стороны, лежит на скелетной линии, а с другой – на прямой, выражаемой уравнением (103), т.е. представляет точку пересечения кривой и прямой (рис9). Такое графическое решение дает достаточно точные результаты

Рис.9 К определению максимальной амплитуды

Рассмотрим теперь случай квадратичного сопротивления.

Квадратичное сопротивление представим выражением.

. (105)

Найдем среднее сопротивление

(106)

Подставим найденное выражение в общие формулы для амплитуды и фазы:

(107)

. (108)

Также как в случае линейного сопротивления амплитуда явно не выражается через частотуω. Поэтому возведем в квадрат обе части уравнения (107) и получим биквадратное уравнение относительно ω.

(109)

Откуда:

(110)

Полагая стоящую под знаком радикала функцию равной нулю, будем иметь

, (111)

С другой стороны:

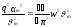. (112)

Решая совместно уравнения (111) и (112) для определения и, найдем :

=() или=().

и

. (113)

Полученные зависимости определяют положение максимума амплитудной кривой при заданных α_m и w.