6 . Приближённые формулы для расчёта периода бортовой качки конечной амплитуды

Для расчёта периода бортовой качки большой амплитуды можно воспользоваться следующими приближёнными формулами:

1) В случае прямобортного судна, когда

,

r– начальный метацентрический радиус.

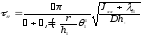, (60)

θ₀– угол крена.

2) В случае прямобортного судна с начальной метацентрической высотой h₀=0, когда

.

. (61)

3) В случае низкобортного судна с относительно большой метацентрической высотой, когда /

. (62)

Данные формулы могут быть использованы в качестве оценочных расчётов.

7. Энергетические зависимости вынужденной качки

Энергетические соотношения, которые имеют место при установившемся колебательном процессе, имеют общий характер и справедливы как для линейных, так и для нелинейных колебаний. Используя эти соотношения, можно дать достаточно строгое приближённое решение дифференциального уравнения, описывающего нелинейный установившейся процесс. Метод, с помощью которого получается это решение, называется методом энергетического баланса [5].

Уравнение бортовой качки на регулярном волнении в относительных координатах имеет вид:

(63)

В данном уравнении момент начала отсчета времени выбран так, чтобы сделать равной нулю начальную фазу вынужденных колебаний, т.е.

Умножим левую и правую части уравнения на величину и проинтегрируем все члены уравнения. Учитывая, что

,

будем иметь

. (64)

Уравнение (63) описывает установившийся процесс бортовой качки на волнении, поэтому в начальный момент времени:

t=0 =0

Тогда:

.

Окончательно, имеем:

. (65)

Полученная зависимость представляет уравнение баланса энергии. Каждая составляющая этого уравнения имеет определённый физический смысл.

1) (-) –приращение кинетической энергии;

2) –работа сил сопротивления;

3) 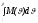–работа восстанавливающих сил (потенциальная энергия);

4) – работа возмущающих сил.

Для установившейся бортовой качки, происходящей с периодом , можно записать две зависимости:

1. При;

. (66)

Тогда из уравнения баланса следует

. (67)

т.е. при максимальном наклонении из положения равновесия разность работ возмущающих сил и сил сопротивления равна разности максимальных значений потенциальной и кинетической энергии.

2)При ;

(68)

Из уравнения баланса энергии следует

(69)

т.е. энергия, сообщаемая кораблю возмущающими силами за один размах, равна работе сил сопротивления за тот же размах.

Рассмотрим интегралы, входящие в полученные выражения. Представим их следующим образом :

. (70)

Рассмотрим поведение функций, входящих в данные интегралы (рис.7)

При установившейся качке график скорости в первой и второй четверти периода будет отличаться только по знаку, но не по абсолютной величине. Тогда, исходя из рисунков, можно определить:

≠0; =0;

=2. (71)

Рис.7 К определению интегралов (70)

Рис.8 К определению интегралов (70)

Функция обладает тем свойством, что абсолютное её значение целиком определяется величиной скорости, а знак функциивсегда соответствует знаку(рис.8), т.е. всегда

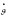
>0 при ≠ 0;

=0 при =0. (72)

Тогда

=2. (73)

Используя полученные значения интегралов (71),(73), подставим их в уравнения (67) и (69). Получим две зависимости:

(74)

. (75)

Разделив на два обе составляющие зависимости (75)и используя её для подстановки в (74), окончательно получим следующие энергетические соотношения:

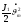-; (76)

. (77)