4. Способы расчёта периода бортовой качки судна с заданной диаграммой остойчивости частотный график качки на спокойной воде
Первая группа способов, включающая в себя первый способ А.Н. Крылова, способы Карпова и Мозли, основана на разбиении всего участка интегрирования на два: большой (от θ до θ1) и малый от θ1 до θ0. На первом участке рассматриваемый интервал нигде в бесконечность не обращается и допускает применение любого из правил приближённого вычисления, например, правила трапеций. Интеграл по второму участку, составляющему незначительную часть первого, рассчитывается отдельно, с помощью специального приближённого приема.
4.1 Способ а.Б. Карпова.
Данный способ допускает применение при нулевой метацентрической высоте. Разбиваем промежуток интегрирования на два участка (рис.1)
θ0= θ1+ Δθ,
Δθ-малый участок, составляющий n-ую часть амплитуды θ0.
.
Участок θ1= Δθ(n-1)
Выражение для периода качки (9) разобьется на два интеграла [1]:
Тθ
=4
,
(10)
Рис.1 Разбиение диаграммы динамической остойчивости по методу Карпова.
Интегрируемая функция в первом интеграле не обращается в бесконечность и поэтому он может быть вычислен по правилу трапеций.
Для этого с диаграммы динамической остойчивости снимаются величины плеч d через интервалы Δθ и вычисляется интеграл I по методу трапеций.
Второй интеграл является не собственным, так как интегрируемая функция обращается в бесконечность при θ=θ0 . Для вычисления второго интеграла делается предположение, что диаграмма динамической остойчивости представляет прямую линию, проходящую через концы ординат d0 и d1. Тогда в интервале между θ1 и θ0 имеем (рис.2)
,
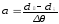(11)
Рис.2 К определению периода качки по методу Карпова.
Но
,
а
.
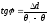Значит
.
С другой стороны
.
Отсюда
.
Тогда второй интеграл можно представить так
, (12)
где
При этом, погрешность расчета получается тем больше, чем круче диаграмма и может быть снижена за счёт уменьшения участка ∆θ.
4.2 Способ Власова в.Г.
Способы второй группы , включающие в себя второй способ А.Н. Крылова, способы Благовещенского, Власова и Робба основаны на замене истинной формы диаграммы остойчивости некоторой аналитической, достаточно простой кривой, для которой рассматриваемый интеграл может быть вычислен аналитически. В способах Робба, Крылова и Благовещенского такими аппроксимирующими кривыми являются параболы соответственно третьей, пятой и n-ой степени. Наиболее простой из способов второй группы– способ В.Г. Власова, основанный на замене истинной, нелинейной диаграммы статистической остойчивости осредненной линейной диаграммой.
Ее плечи лежат посредине между хордой OB и секущей OC,отсекающей площадь, равную площади истинной диаграммы для того угла крена θ0, для которого вычисляется период θ. В результате осреднённое плечо статистической остойчивости:
,
(13)
так как согласно рис.3, будем иметь
S∆оас=d0=
.
(14)
Отсюда,
.
Рис.3 К определению периода качки по методу Власова.
Для периода качки судов с такой диаграммой справедлива формула линейной теории
(15)
Но
hср=
,
поэтому окончательное выражение для
периода будет иметь вид:
,
(16)
Угол θ0 берется в радианах.
Способом Власова можно пользоваться для амплитуд θ0 не превышающих положение максимума диаграммы [3].
Способы третьей группы (Павленко и Сизова) основаны на заменах переменной интегрирования, устраняющих несобственность вычисляемого интеграла.