3. Бортовая качка конечной амплитуды на спокойной воде. Формула для периода качки

В общем случае качки судна на спокойной воде бортовые колебания конечной амплитуды сопровождаются поперечно-горизонтальными, вертикальными колебаниями и рысканием. Более того, из-за взаимосвязи вертикальных колебаний с килевыми и продольно-горизонтальными при бортовой качки конечной амплитуды возникают все пять остальных видов качки. Однако опыты показывают, что для достаточно удлиненных судов влияние килевых, продольно-горизонтальных колебаний и рысканья на кинематику бортовой качки на спокойной воде, как правило, невелико. Гидродинамическая взаимосвязь бортовой качки с поперечно-горизонтальной и вертикальной очень сложна; учёт этой взаимосвязи требует решения нелинейной гр. задачи с использованием разложений в ряды по малому параметру. Но, в первом приближении влияние поперечно-горизонтальных колебаний на характер бортовых может быть оценено в рамках линейной теории, а влияние вертикальной качки сведено к учету неравно объемности бортовых наклонений, которое на кинематических характеристиках качки существенно не сказывается. Эти допущения лежат в основе упрощенного подхода и составлению и решению дифференциального уравнения бортовой качки конечной амплитуды на спокойной воде.

Будем считать, что другие виды качки отсутствуют, а бортовые наклонения судна равнообъемные. Тогда на смоченную поверхность судна действуют:

1. восстанавливающий момент: _,

2. инерционный:

3. демпфирующий:

Условие динамического равновесия действующих на судно моментов приводит к уравнению

(1)

- момент инерции массы судна относительно центральной продольной оси.

При достаточно больших амплитудах, превышающих угол входа палубы в воду, присоединенный момент инерции может зависеть от угла качки. Однако модельный эксперимент показывает, что в большинстве случаев для судов обычных образований они весьма слабы. Поэтому будем считатьпостоянным, не зависящим от угла качки.

Демпфирующий момент является сложной функцией угловой скорости качки: в отличие от линейной теории Мс может зависеть от квадрата и даже куба . Однако для большинства морских судов величинасказывается только на степени затухания бортовых колебаний. Ставя основной задачей, определение периода качки на спокойной воде, сопротивлением воды качке судна пренебрегаем. Тогда уравнение (1) примет вид:

(2)

или

где 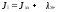- суммарный момент инерции массы судна и присоединенной массы воды.

Сложность данного уравнения в том, что оно нелинейное, причем l(θ) обычно задается не аналитически, а таблично или графически.

Чтобы получить формулу для периода качки проинтегрируем это уравнение:

1. Заменим

2. Помножим правую часть на

(3)

Введем (3) в уравнение

Переменные илегко разделить

(4)

Проинтегрируем равенство (4) при следующих начальных условиях t=0,θ=θ₀, =0.

Это означает, что процесс качки на тихой воде происходит благодаря начальному отклонению судна на угол θ₀ и предоставлению его затем самому себе. Тогда, интегрируя левую часть от =0 до текущего значения угловой скорости , и правую отθ=θ₀ до текущего угла качки θ, получим

или

(5)

Откуда получим

(6)

Здесь d=d(θ)– плечо динамической остойчивости;d₀=d(θ₀)

Это равенство имеет простую физическую интерпретацию: приращение в процессе качки кинетической энергии системы судно-жидкость равно изменению потенциальной энергии. Для определения второго интеграла уравнения качки представим полученное равенство в виде [3]:

,

.

отсюда

(7)

Из физических соображений необходимо оставить только знак “–“, поскольку при заданных начальных условиях приращению времени отвечает уменьшение угла θ , т.е. отрицает значение dθ .

Проинтегрируем (7) от t=0 до текущего момента времени t при тех же начальных условиях. Тогда получим:

(8)

Рассматриваемый процесс качки является незатухающим периодическим. Обозначим его период τ_θ . Тогда при θ=0 судно оказывается в прямом положении, т.е. проходит четверть полного периода колебания, за время . Используя это значениеt в формуле (8), находим искомый период качки

(9)

Интеграл, стоящий в правой части, является несобственным так как при θ=θ₀ подинтегральная функция обращается в бесконечность. Для вычисления данного интеграла разработан ряд способов, которые можно разбить на три принципиально различные группы.