11.1.2 Субгармонический резонанс третьего рода

_{Колебания судна в режиме субгармонического резонанса третьего рода обусловлены нелинейными свойствами диаграммы остойчивости и могут возникнуть лишь тогда, когда последние выражены достаточно сильно. Чем слабее нелинейность начального участка диаграммы, тем меньше вероятность появления этого резонанса. Поэтому субгармонический резонанс третьего рода маловероятен при качке судов со значительной начальной остойчивостью и, по-видимому, возможен при качке судов с малой метацентрической высотой и резковыраженной S-образной ДСО. Этот резонанс характерен для зоны частот волнения, которые примерно в 3 раза больше частот собственных колебаний судна.}

_{Т.о., данный резонансный режим может быть вызван действием набегающих волн мертвой зыби, ещё более коротких, чем в случае параметрического резонанса. Однако качка судна в этом режиме будет происходить с частотой, достаточно близкой к частоте собственных бортовых колебаний. Форма резонансных колебаний судна будет иметь сложный, полигармонический характер.}

_{Рис.18 АЧХ бортовой качки в основном и субгармонических резонансных режимах второго и третьего рода.}

_{Сопоставление амплитудно-частотных кривых различных режимов качки показывает принципиальное отличие амплитудно-частотной кривой резонанса третьего рода от рассмотренных ранее: демпфирование ограничивает эту кривую не только сверху, как при основном и параметрическом резонансах, но и снизу, превращая её в замкнутую (рис.18). Это значит, что плавное, медленное изменение частоты волнения не может привести к возникновению резонанса 3 рода- для этого необходимо дополнительное внешнее воздействие, например, шквал ветра или отдельная крутая волна.}

_{Попытки экспериментального изучения резонанса третьего рода в опытовом бассейне не увенчались успехом. Поэтому о нем можно говорить как о теоретически возможном, но ещё не подтвержденном экспериментом.}

_{Можно показать, что участки резонансных кривых, для которых не выполняются условия [4]:}

при ;

при. (178)

отвечают неустойчивым физически нереальным режимам колебаний.

11.2 Супергармонический резонансный режим

_{Супергармонические резонансы, в отличие от субгармонических возникают в результате многочастотного возбуждения ( наличия высших гармоник в выражении для возмущающего момента).}

_{Рассмотрим уравнение бортовой качки в абсолютных координатах с учетом возмущающего момента второго порядка.}

₍₁₇₉₎

_{Нелинейный момент второго порядка} определяется на основании решения общей нелинейной задачи о поперечной качке плоского контура на регулярном волнении с учетом нелинейных граничных условий на самом контуре и свободной _{поверхности жидкости [ 6].}

_{Решение данного уравнения будем искать в следующем виде :}

₍₁₈₀₎

_{Дифференцируя (180) , подставляя найденные производные в (179) и отделяя составляющие одного порядка малости получим :}

₍₁₈₁₎

₍₁₈₂₎

_{Решение уравнения (181) определяет амплитуды бортовой качки в основном резонансном режиме, а решение уравнения (182)- в супергармоническом резонансном режиме. Перепишем уравнение (182) следующим образом :}

₍₁₈₃₎

_где

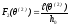
_{Применяя метод гармонического баланса для решения данного уравнения , после несложных выкладок, можно получить следующие уравнения установления бортовой качки в супергармоническом резонансном режиме :}

(184)

(185)

Полученные выражения представляют собой законы изменения во времени амплитуд и фаз второй гармоники бортовой качки. Правые части полученных выражений являются периодическими функциями по , которые могут быть представлены в виде рядов Фурье .Применяя затем принцип усреднения за период, окончательно будем иметь:

(186)

Рассмотрим стационарный режим качки, в котором амплитуды и фазы являются постоянными величинами

Тогда будем иметь

(187)

где

(188)

Ясно, что

Тогда систему уравнений (187) можно переписать так

(189)

Из систем уравнений (189) легко получить выражения для искомых амплитуд и фаз

(190)

(191)

Уравнение (190) следует представить в виде биквадратных уравнений относительно частот  и для построения АЧХ использовать обратную зависимость частоты от амплитуды. Возводя в квадрат правые и левые части выражения (190) после несложных преобразований получим:

(192)

Откуда

(193)

Остановимся подробнее на вычислении нелинейного момента _.

_{В соответствии с методом малого параметра [6]:} (194)

где

- малые параметры, характеризующие относительные амплитуды волнового движения жидкости, поперечно-горизонтальных, вертикальных и бортовых колебаний.

В выражении ( 194) :

–момент второго порядка, обусловленный взаимодействием набегающих и дифрагированных волн;

моменты, обусловленные изолированными ПГК, ВК и БК контура на тихой воде;

моменты, обусловленные взаимодействием набегающего, дифрагированного и вызванного колебаниями контура волнения жидкости;моменты второго порядка, обусловленные совместными ПГК и ВК, ПГК и БК, ВК и БК на тихой воде.

Все составляющие нелинейного момента определяются на основании гипотезы плоских сечений, согласно которой все нелинейные задачи решались вначале для отдельного шпангоутного сечения, а затем найденные гидродинамические характеристики интегрировались по длине судна.

Для каждого шпангоутного контура составляющие нелинейного момента определяются согласно следующим выражениям [6] :

(195)

(196) (197)

где

;

(198)

где

;

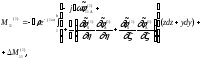(199)

где

_;

(200)

,

где

(201)

,

где

(202)

,

где

В формулах (195) – (202) ипредставляют собой комплексные амплитуды вертикальной, поперечно-горизонтальной и бортовой качки, определяемые на основании решения задачи первого порядка.

Все потенциалы второго порядка , входящие в выражения для составляющих момента могут быть определены на основании метода интегральных уравнений с учетом нелинейных граничных условий на свободной поверхности жидкости и на контуре. Представим каждый потенциал второго порядка в комплексном виде . Тогда система интегральных уравнений будет иметь вид :

(203)

m=2,3,4,7; k=2,3,4,7,

где путь интегрирования Г означает участок невозмущенной свободной поверхности y=0, исключая участок пересечения ее контуром .

Функция Грина для задачи второго порядка имеет вид:

(204)

где

Разбивка контура на сегменты позволяет перейти от этой системы к системе 2N связанных алгебраических уравнений для :

(205)

I=1, 2,...,N,

где

(206)

Знак ± в выражениях (206) выбирается в соответствии с условием симметрии потенциалов второго порядка и функций относительно вертикальной оси контура.

Так при определении потенциалов и симметричных частей потенциалов необходимо оставить знак “+”. При определении потенциалов и асимметричных частей потенциаловнеобходимо использовать знак “-”.

Нижний предел интегралов (206) равен b/2 в случае пересекающего свободную поверхность контура

Здесь идействительные и мнимые части функций, представляющих собой граничные условия на свободной поверхности в задачах второго порядка.

Когда m=k=2,3,4:

(207)

При

(208)

Когда m=k=7:

((209)

В случае m=2,3,4; k=0+7:

(210)

где 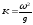- волновое число;

Функции . ипредставляют собой действительные и мнимые части граничных условий на контуре:

(211)

(212)

(213)

(214)

(215)

(216)

; (217)

(218)

(219)

. (220)

Коэффициенты , входящие в систему (205) определяются следующим образом

(221)

(222)

(223)

(224)

Входящие сюда интегралы легко вычисляются по формулам квадратур благодаря тому, что путь Sj-прямолинейный сегмент.

Таким образом, для построения амплитудно-частотной характеристики необходимо задаться рядом значенийпо кривой частотнайти соответствующие значения собственных частоти затем по формуле (193) вычислить значения частот возмущения. Построенная таким образом криваябудет представлять зависимость амплитуд бортовой качки от частоты в супергармоническом резонансном режиме.

При вычислении по формулам (193), необходимо иметь в виду, что значения нелинейных возмущающих моментов, входящих в правые части данных выражений, зависят от частоты. Указанное обстоятельство вынуждает рассчитывать зависимость 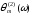методом последовательных приближений согласно которому в первом приближении в правых частях уравнений следует положитьи вычислять действительные и мнимые составляющие моментовкак функции , зависящие от.

Построенные в первом приближении амплитудно-частотные характеристики качки в супергармоническом резонансном режиме необходимо уточнить. Для этого в каждом последующем приближении, нелинейные моменты 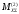следует вычислять как функции, зависящие от частот, найденных в предыдущем приближении.. Для получения окончательных значений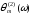обычно достаточно второго и третьего приближения соответственно.

Выражение для кривой, определяющей положение максимума имеет вид:

(225)

Используя метод вариаций Ляпунова , условия устойчивости в малом для качки в супергармоничском резонансном режиме будут иметь вид [6]:

при ;

при (226)

На рис. 19-22 приведены результаты расчетов амплитуд бортовой качки в основном и супергармоническом резонансных режимах для четырех различных судов. Также показан расчет суммарной амплитудно-частотной характеристики, учитывающей влияние вторых гармоник.

Анализ результатов расчетов амплитуд бортовой качки в супергармоническом резонансном режиме, проведенных для различных типов судов, позволил сделать следующие выводы:

1. максимальные амплитуды качки в супергармоническом резонансном режиме возникают на частотеи не превышают 10-15 градусов ( рис.19-22);

2. нелинейность по восстанавливающему моменту в большинстве случаев не влияет на значения амплитуд вторых гармоник , поскольку при 15 град. собственная частота нелинейной бортовой качки практически не зависит от угла крена и может быть вычислена по линейной теории. Поэтому для кривых не характерен загиб в сторону низких или высоких частот. Кроме этого, значения полученных амплитудпрактически полностью совпадают с соответствующими значениями, найденными в результате решения системы , учитывающей нелинейность, вызванную только действием гидродинамических сил второго порядка

3. кривая зависимости соответствует устойчивым “ в малом” режимам качки.

Амплитудно-частотные характеристики бортовой качки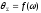, соответствующие бигармоническому закону колебаний (180), были определены посредством суммирования значений амплитуд первой и второй гармоник, снятых с соответствующих кривых с учетом малого параметра[6]. Полученные таким образом АЧХ имеют соответственно два резонансных режима: основной и супергармонический. В зоне последнего амплитуды бортовой качкидля судов с большим значением отношенияB/T , малой метацентрической высотой h_o и S- образной диаграммой остойчивости могут

быть в два раза больше соответствующих амплитуд, определенных без учета нелинейных гидродинамических сил второго порядка Для судов со значительной начальной остойчивостью (h_o3,5м ) учет нелинейных

факторов в зоне супергармонического резонанса приводит к увеличению амплитуд по сравнениювсего на 2-5градуса.

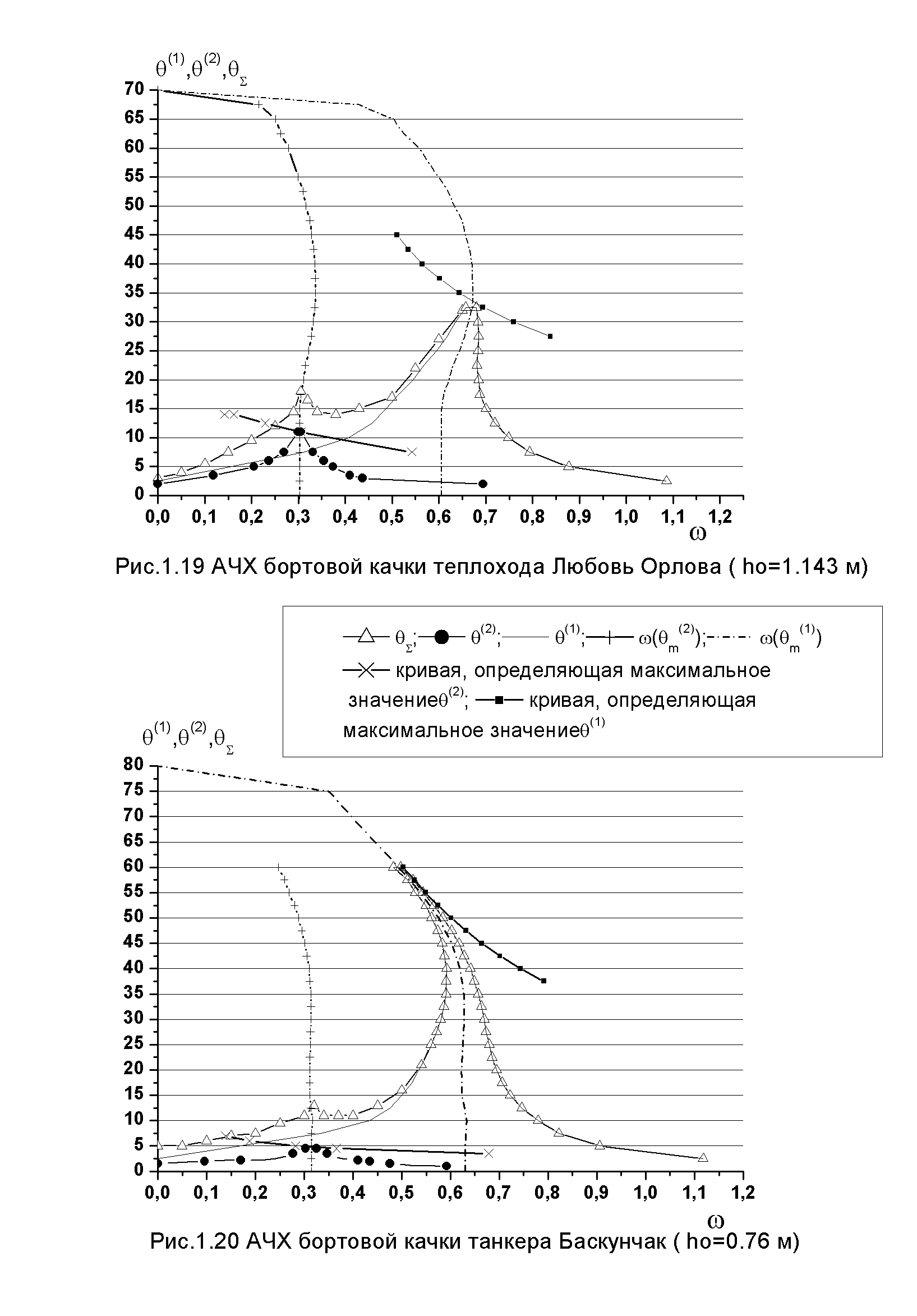
Рис.19 АЧХ бортовой качки теплохода Любовь Орлова

Рис.20 АЧХ бортовой качки танкера Баскунчак

_{Рис.21 АЧХ бортовой качки контейнеровоза Художник Сарьян}

_{Рис.22 АЧХ бортовой качки судна Волго-Балт}