
методические указания для лабораторных работ / РАСЧЕТ СОБСТВЕННЫХ И ВЗАИМНЫХ ЧАСТИЧНЫХ ЕМКОСТЕЙ СИСТЕМЫ ПРОВОДНИКОВ
.pdf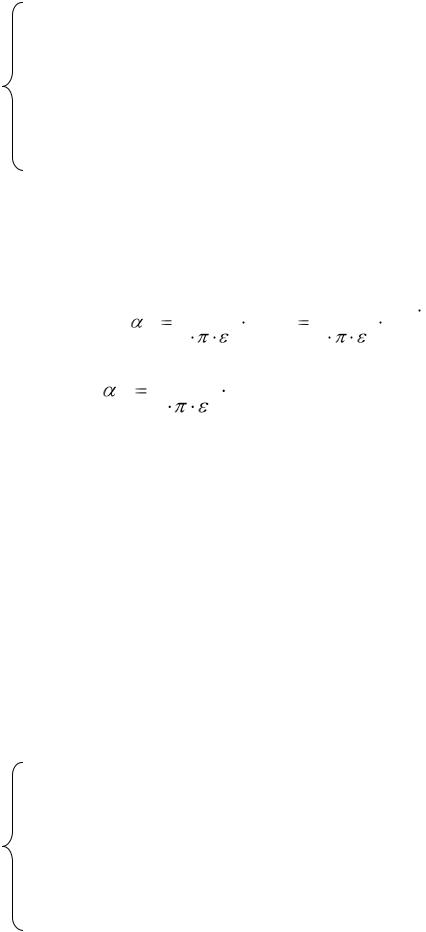
1= 11 1+ 12 2 + 13 3 + 14 4 + 15 5
2= 21 1+ 22 2 + 23 3 + 24 4 + 25 5
3= 31 1+ 32 2 + 33 3 + 34 4 + 35 5
(7)
4= 41 1+ 42 2 + 43 3 + 44 4 + 45 5
5= 51 1+ 52 2 + 53 3 + 54 4 + 55 5
Коэффициенты системы определяются аналогично (6), а индексы коэффициентов - взаимными расстояниями проводников. Для одинаковых
индексов (k = n): kk |
|
1 |
ln |
bkk |
|
|
1 |
ln |
2 hk |
, |
(8) |
|
|
akk |
|
|
|
|
|||||
|
2 |
a |
|
2 |
a |
|
r k |
|
|||
а для разных: |
|
1 |
|
ln |
bkn |
. |
(9) |
kn |
2 |
|
akn |
||||
|
|
||||||
|
|
a |
|
|
|
Коэффициенты с одинаковыми индексами 11, 22, …, kk опреде-
ляют потенциал проводникам его собственным линейным зарядом, а коэф-
фициенты с разными индексами определяют составляющую потенции-
kn
ала проводника от влияния зарядов соседних проводников. Присвоение ин-
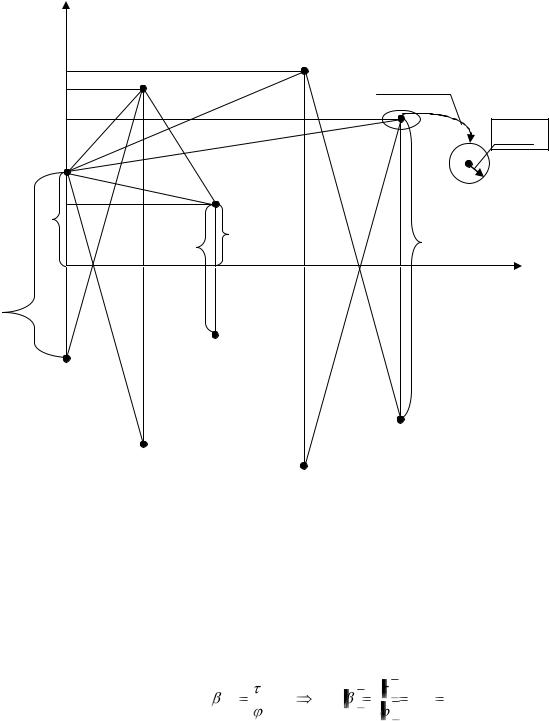
дексов расстояниям a и b иллюстрируется рис. 2.
Коэффициенты называются потенциальными коэффициентами. Ес-
ли все потенциальные коэффициенты системы (7) определены, а потен-
циалы всех проводников известны, то система допускает решение отно-
сительно неизвестных линейных плотностей зарядов проводников:
1= 11 1+ 12 2 + 13 3 + 14 4 + 15 5
2= 21 1+ 22 2 + 23 3 + 24 4 + 25 5
3= 31 1+ 32 2 + 33 3 + 34 4 + 35 5 (10)
4= 41 1+ 42 2 + 43 3 + 44 4 + 45 5
11
5= 51 1+ 52 2 + 53 3 + 54 4 + 55 5
Уравнения системы (10) называются второй группой формул Макс-
велла, а коэффициенты системы - емкостными коэффициентами. Если
b11 =2 h1
y, м |
|
|
|
|
|
|
|
y1 |
|
|
|
|
4 |
увеличено |
|
y2 |
|
2 |
|
a14 |
|
||
a21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y5 |
a12 |
|
|
|
|
|
|
|
|
a15=a51 |
|
5 |
r5 |
||
1 |
|
|
|
a23= a32 |
b45 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
y1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
b33 |
h3 = y3 |
|
b55=2 h5 |
|
|
|
b21 |
|
|
x, м |
|||
|
|
|
|
|
|
||
|
b12 |
x2 |
|
x3 |
x4 |
x5 |
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
b54 |
|
|
|
|
|
|
|
|
5 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
Рис. 2. Правило присвоения индексов расстояниям а и b:
аkn – расстояние от проводника k до проводника n; bkn - расстояние от проводника k до изображения проводника n; bkk расстояние от проводника k до изображения проводника k; rk – радиус проводника k
положить 1 0, а 2= 3= 4= 5=0, то из первого уравнения системы:
|
|
|
|
|
|
|
К |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
м |
|
||||
1= 11 1 |
11 |
|
|
|
|
|
|
|
|
|
. |
(11) |
1 |
|
|
|
В |
|
м |
||||||
12

Таким образом, коэффициенты имеют размерность емкости на единицу длины проводника. Все коэффициенты могут быть вычислены через известные коэффициенты :
kn  kn , (12)
kn , (12)
где - главный определитель системы (7),
– алгебраическое дополнение определителя , которое образуется
kn
вычеркиванием k-й строки и n-го столбца и умножением полученного минора на (-1)k+n.
При всех вычислениях главный определитель получается симметрич-
ным относительно главной диагонали. Симметрия обуславливается равен-
ством расстояний akn = ank и расстояний bkn = bnk и, как следствие, равен-
ством коэффициентов и . Из симметрии главного определителя сле-
kn nk
дует равенство алгебраических дополнений = и коэффициентов
kn nk
= . Все коэффициенты с одинаковыми индексами положительны,
kn kn kk
а с разными – отрицательны.
kn
Уравнения системы (10) в результате эквивалентных преобразований могут быть сведены к третьей группе формул Максвелла. Для примера такие преобразования показаны ниже для первого уравнения системы (10)
прибавлением и вычитанием из уравнения одинаковых произведений:
1= 11 1+ 12 2 + 13 3 + 14 4 + 15 5 + + 12 1 - 12 1 + 13 1 - 13 1 + 14 1 - 14 1 +
15 5 - 15 5 = = ( 11+ 12 + 13 + 14 + 15) 1+ 12 ( 2- 1) + 13 ( 3- 1) +
14 ( 4- 1) + 15 ( 5- 1) = ( 11+ 12 + 13 + 14 + 15) 1-
12 ( 1- 2) - 13 ( 1- 3) |
|
|
С11 |
U12 |
U13 |
13

- 14 ( 1- 4) - 15 ( 1- 5) = C11 1+ C12 U12 + C13 U13 + C14 U14 +
U14 U15
+C15 U15.
(13)
Напряжения U12, U13, …, U1k есть разность потенциалов между первым и k-м проводом, а С12, С13, …, С1k – емкость между теми же проводами на единицу их длины. Они называются взаимными частичными емкостями. Емкость С11 называется собственной частичной емкостью для провода №1, ей соответствуют одинаковые индексы в обозначении. Физически соб-
ственная частичная емкость обусловлена взаимным расположением прово-
да и проводящей поверхности.
Подобные преобразования можно выполнить для остальных урав-
нений системы (10), в результате чего получается система (14).
Уравнения системы (14) называются третьей группой формул Максвелла. По аналогии с первым уравнением коэффициенты Сkk системы (10) с оди-
наковыми индексами называются собственными частичными емкостями, а с разными индексами Сkn – взаимными частичными. Уравнения
1 = C11 1+ C12 U12 + C13 U13 + C14 U14 + C15 U15
2 = C21 U21+ C22 2 + C23 U23 + C24 U24 + C25 U25
3 = C31 U31+ C32 U32 + C33 3 + C34 U34 + C35 U35
(14)
4 = C41 U41+ C42 U42 + C43 U43 + C44 4 + C45 U45
5 = C51 U51+ C52 U52 + C53 U53 + C54 U54 + C55 5
системы позволяют составить схему замещения для группы линий (осей), которая показана на рис. 3. Для простоты на рисунке показана только часть емкостей и их обозначение индексами.
y, м
|
2 |
С24 = С42 14 |
4 |
С45 = С54 |
|
|
|
||
С12 |
|
С14 |
|
5 |

Рис. 3. К понятию собственных и взаимных частичных емкостей
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
Выполнить расчет собственных, взаимных частичных емкостей и ли-
нейных плотностей зарядов системы проводников для следующего вари-
анта задания:
|
|
|
Номер провода |
|
|
||
Параметры |
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
4 |
5 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x, м |
0 |
0,2 |
|
0,6 |
|
1,1 |
1,3 |
|
|
|
|
|
|
|
|
y, м |
0,5 |
0,7 |
|
0,9 |
|
0,4 |
1,1 |
|
|
|
|
|
|
|
|
r, мм |
5 |
10 |
|
5 |
|
10 |
10 |
|
|
|
|
|
|
|
|
, В |
140 |
80 |
|
200 |
|
70 |
105 |
|
|
|
|
|
|
|
|
Рекомендуется выполнять расчет с применением пакета прикладных программ. Ниже приведен вариант расчета с применением программы
Mathcad (по желанию студента допускается ручной расчет). В расчете приведены краткие текстовые комментарии и пояснения.
Координаты точек (м):
x1 |
0 |
x2 |
0.2 |
x3 |
0.6 |
x4 |
1.1 |
x5 |
1.3 |
y1 |
0.5 |
y2 |
0.7 |
y3 |
0.9 |
y4 |
0.4 |
y5 |
1.1 |
|
|
|
|
|
15 |
|
(задание координат и |
||
|
|
|
|
|
|
|
радиусов проводников |
||
kr1 |
1 0.5005 |
nr2 |
10.0105 |
r3 |
0.005 |
r4в матричной0.010 r5форме0.01) |
|||
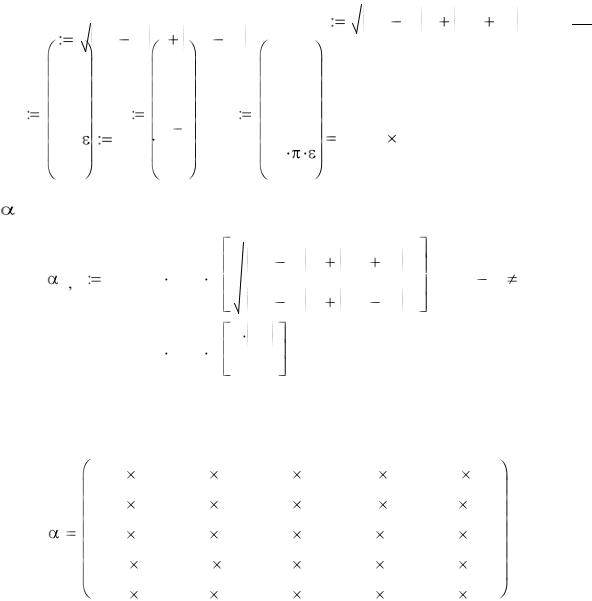
Радиусы проводников (м):
Расчет расстояний akn и bkn по теореме Пифагора по рис. 2 ORIGIN  1 (присвоение индексов начать с 1)
1 (присвоение индексов начать с 1)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
x |
x 2 |
y |
y 2 |
||
|
|
|
|
|
|
|
|
|
|
||||||||
a |
|
x |
x |
2 |
y |
y |
2 |
|
kn |
|
k |
n |
k |
n |
|||
|
|
|
|
|
|
|
|
|
|
||||||||
kn |
0 |
k |
n |
0.5 |
k |
n |
|
|
0.005 |
|
|
Расчет коэффициента |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0.2 |
|
|
0.7 |
|
|
|
|
0.01 |
|
выражения (6): |
|
|
||||
x |
0.6 |
y |
|
0.9 |
|
r |
|
|
0.005 |
|
|
|
|
|
|
|
|
|
|
8.85 10.412 |
|
|
|
1 |
|
1.798 |
1010 |
|
|
|
|||||
|
1.1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
0.01 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1.3 |
|
|
1.1 |
|
|
|
|
0.01 |
|
|
Расчет коэффициентов |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
kn:
1
2

|
|
|
|
|
x |
x |
2 |
y |
y |
n |
2 |
|
|
1.798 |
1010 ln |
|
|
k |
n |
|
k |
|
|
if k n 0 |
|
k n |
|
|
|
|
|
|
|
|
|
|||
|
|
x |
x |
2 |
y |
y |
n |
2 |
||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
k |
n |
|
k |
|
|
|
|
|
1.798 |
1010 ln |
2 yk |
otherwise |
|
|
|
|
||||
|
|
|
rk |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Результаты расчета потенциальных коэффициентов в матричной форме:
9.526 |
1010 |
2.623 |
1010 |
1.344 |
1010 |
4.533 |
109 |
6.554 |
109 |
2.623 |
1010 |
8.885 |
1010 |
2.346 |
1010 |
7.268 |
109 |
1.059 |
1010 |
1.344 |
1010 |
2.346 |
1010 |
1.058 |
1011 |
1.219 |
1010 |
1.921 |
1010 |
4.533 |
109 |
7.268 |
109 |
1.219 |
1010 |
7.879 |
1010 |
1.316 |
1010 |
6.554 |
109 |
1.059 |
1010 |
1.921 |
1010 |
1.316 |
1010 |
9.698 |
1010 |
Таким образом, все потенциальные коэффициенты системы (7) най-
дены, поэтому возможно решение системы относительно неизвестных ли-
16
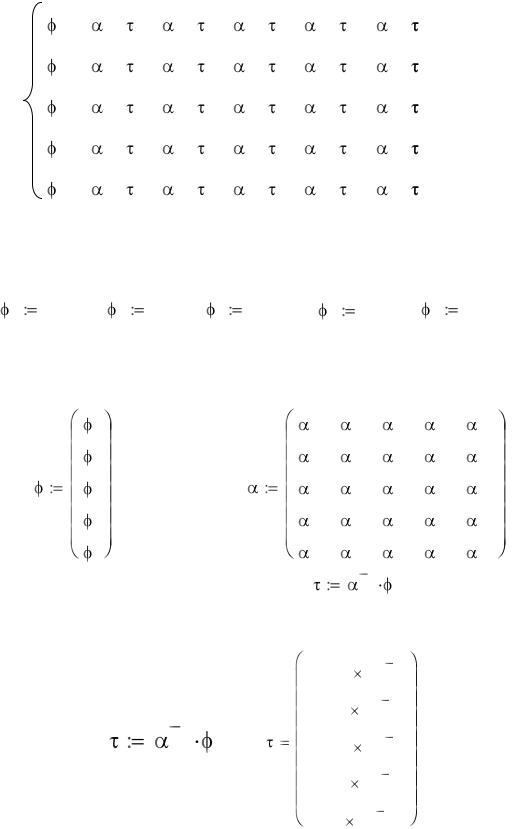
нейных плотностей зарядов . В программе Mathcad система (7) запишется в виде:
1 11
11 1
1  12
12 2
2  13
13 3
3  14
14 4
4  15
15 5
5
2 21
21 1
1  22
22 2
2  23
23 3
3  24
24 4
4  25
25 5
5
3 31
31 1
1  32
32 2
2  33
33 3
3  34
34 4
4  35
35 5
5
4 41
41 1
1  42
42 2
2  43
43 3
3  43
43 4
4  45
45 5
5
5 51
51 1
1  52
52 2
2  53
53 3
3  54
54 4
4  55
55 5
5
Потенциалам осей присваиваются численные значения в соответствии с вариантом задания:
1 |
140 |
2 |
80 |
3 |
200 |
4 |
70 |
5 |
105 |
Систему удобно решать в матричной форме, поэтому потенциалы осей записываются как вектор-столбец, а коэффициенты - как матрица:
1 |
11 |
12 |
13 |
14 |
15 |
2 |
21 |
22 |
23 |
24 |
25 |
3 |
31 |
32 |
33 |
34 |
35 |
4 |
41 |
42 |
43 |
44 |
45 |
5 |
51 |
52 |
53 |
54 |
55 |
Применяя стандартный алгоритм ( |
1 |
) программы Mathcad для |
|
||
решения системы уравнений, вычисляют искомые значения : |
||
1.176 |
10 |
9 |
2.635 |
10 |
11 |
1 |
|
9 |
1.566 |
10 |
|
4.714 |
10 |
10 |
6.26 |
10 |
10 |
17
В результате все линейные плотности зарядов найдены.
Емкостные коэффициенты рассчитываются в соответствии с (12):
kn
kn
где - главный определитель системы (7),
– алгебраическое дополнение определителя , которое образуется
kn
вычеркиванием k-й строки и n-го столбца и умножением полученного минора на (-1)k+n.
Главный определитель образуется на основе матрицы . Для
исключе-
ния путаницы в обозначении элементов матрицы и ее субматриц,
образу-ющих миноры определителей kn, переобозначим матрицу |
|
символом А, то есть А. Тогда, А и = 5.445 1054. |
|
Коэффициентов , а значит и алгебраических дополнений ( ) - 25.
kn kn
Приводить их все не имеет смысла, так как они образуются по известному
простому правилу. Ниже приведен пример записи для двух субматриц.
|
|
22 |
23 |
24 |
25 |
21 |
23 |
|
24 |
25 |
|||||||||
A11 |
32 |
33 |
34 |
35 |
31 |
33 |
|
34 |
35 |
||||||||||
|
|
|
|
|
|
A12 |
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
42 |
43 |
44 |
45 |
41 |
43 |
|
44 |
45 |
|||||||||
|
|
52 |
53 |
54 |
55 |
51 |
53 |
|
54 |
55 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
11 = А11 |
|
12 = А12 |
|
|||||||||||||
В соответствии с (12): |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
11 |
|
A11 |
|
11 =1.149 10-11 |
12 |
|
|
|
A12 |
|
12 3.162 10-12 |
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
A |
|
|
|
|
|
A |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Аналогично вычисляются все остальные коэффициенты. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
13 |
|
A13 |
|
13 6.853 10-13 |
14 |
|
A14 |
|
|
|
14 2.191 10-13 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
A |
|
|
|
|
A |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
18
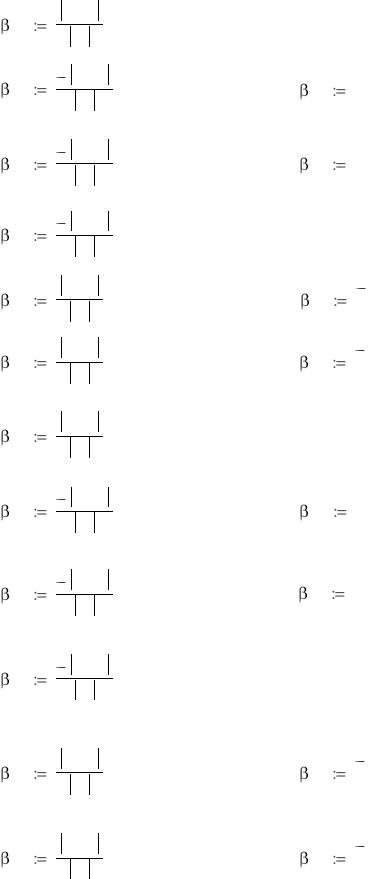
15
A15
A
21
A21
A
23
A23
A
25
A25
A
31
A31
A
33
A33
A
35
A35
A
41
A41
A
43
A43
A
45
A45
A
51
A51
A
53
A53
A
15 2.659 10-13
21 3.162 10-12 |
22 |
|
|
|
A22 |
|
|
|
|
|
|
22 1.291 10-11 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
A |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
23 2.276 10-12 |
24 |
|
|
|
A24 |
|
|
|
|
|
|
|
24 5.448 10-13 |
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
A |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
25 6.716 10-13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 6.853 10-13 |
32 |
|
|
|
|
|
A32 |
|
32 2.276 10-12 |
|||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
A |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
33 1.046 10-11 |
34 |
|
|
|
|
A34 |
|
|
|
34 1.097 10-12 |
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
A |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
35 1.628 10-12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 2.191 10-13 |
42 |
|
|
|
A42 |
|
|
|
|
42 5.448 10- |
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
A |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
13 |
|||||
43 1.097 10-12 |
44 |
|
|
|
A44 |
|
|
|
|
|
44 1.317 10-11 |
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
A |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
45 1.495 10-12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
51 2.659 10-13 |
52 |
|
|
|
|
|
A52 |
|
|
52 6.716 10-13 |
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||
53 1.628 10-12 |
54 |
|
|
|
|
A54 |
|
|
54 1.495 10-12 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
19

55 |
|
A55 |
|
55 1.093 10-11 |
||
|
|
|
|
|
||
|
|
A |
|
|
||
|
|
|
|
|
|
|
Емкостные коэффициенты второй группы формул Максвелла вычис-лены. В соответствии с (13) вычисляются собственные частичные емкости проводов:
C11 |
11 |
12 |
13 |
14 |
15 |
С11 7.159 10-12 |
C22 |
21 |
22 |
23 |
24 |
25 |
С22 6.257 10-12 |
C33 |
31 |
32 |
33 |
34 |
35 |
С33 4.774 10-12 |
C44 |
41 |
42 |
43 |
44 |
45 |
С44 9.816 10-12 |
C55 |
51 |
52 |
53 |
54 |
55 |
С55 6.865 10-12 |
В соответствии с обозначением взаимных частичных емкостей в (13),
вычисляются их значения:
C12 |
12 |
C12 |
3.162 |
10 |
12 |
C34 |
34 |
C34 |
1.097 |
10 |
12 |
C13 |
13 |
C13 |
6.853 |
10 |
13 |
C35 |
35 |
C35 |
1.628 |
10 |
12 |
C14 |
14 |
C14 |
2.191 |
10 |
13 |
C41 |
C14 |
C41 |
2.191 |
10 |
13 |
C15 |
15 |
C15 |
2.659 |
10 |
13 |
C42 |
C24 |
|
|
|
|
C21 |
C12 |
C21 |
3.162 |
10 |
12 |
C43 |
C34 |
C43 |
1.097 |
10 |
12 |
C23 |
23 |
C23 |
2.276 |
10 |
12 |
C45 |
45 |
C45 |
1.495 |
10 |
12 |
C24 |
24 |
C24 |
5.448 |
10 |
13 |
C51 |
C15 |
C51 |
2.659 |
10 |
13 |
C25 |
25 |
C25 |
6.716 |
10 |
13 |
C52 |
C25 |
C52 |
6.716 |
10 |
13 |
C31 |
C13 |
C31 |
6.853 |
10 |
13 |
C53 |
C35 |
C35 |
1.628 |
10 |
12 |
C32 |
C23 |
C32 |
2.276 |
10 |
12 |
C54 |
C45 |
C54 |
1.495 |
10 |
12 |
Коэффициент С42 в результатах расчета отсутствует, так как оператор присваивания ссылается на значение, полученное в строке ниже (7-я стро-
ка). Для получения результата достаточно повторить запись С42 С24
ниже седьмой строки:
C42  C24 С42 = 5.448 10 13
C24 С42 = 5.448 10 13
20
