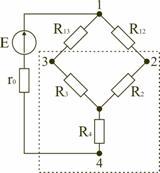
6 Преобразование треугольника сопротивлений в эквивалентную звезду

В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме. Сопротивления R₁₂, R₁₃, R₂₄, R₃₄ включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.

В мостовой схеме сопротивления R₁₃, R₁₂, R₂₃ и R₂₄, R₃₄, R₂₃ соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R₂₄ R₃₄ R₂₃ звездой R₂ R₃ R₄. Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:

; ;.

7 Преобразование звезды сопротивлений в эквивалентный треугольник

Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:

; ;.

После проведенных преобразований можно определить величину эквивалентного сопротивления мостовой схемы

.

8. Расчет электрических цепей постоянного тока с одним источником методом свертывания

Этот метод применяется для не очень сложных пассивных электрических цепей, такие цепи встречаются довольно часто, и поэтому этот метод находит широкое применение. Основная идея метода состоит в том, что электрическая цепь последовательно преобразуется ("сворачивается") до одного эквивалентного элемента, и определяется входной ток. Затем осуществляется постепенное возвращение к исходной схеме ("разворачивание") с последовательным определением токов и напряжений.

Последовательность расчёта:

1. Расставляются условно–положительные направления токов и напряжений.

2. Поэтапно эквивалентно преобразуются участки цепи. При этом на каждом этапе во вновь полученной после преобразования схеме расставляются токи и напряжения в соответствии с п. 1.

3. В результате эквивалентного преобразования определяется величина эквивалентного сопротивления цепи.

4. Определяется входной ток цепи с помощью закона Ома.

5. Поэтапно возвращаясь к исходной схеме, последовательно находятся все токи и напряжения.

Рассмотрим этот метод на примере. В исходной схеме расставляем условно–положительные направления токов в ветвях и напряжений на элементах. Нетрудно согласиться, что под действием источника E с указанной полярностью направление токов и напряжений такое, какое показано стрелками. Для удобства дальнейшего пояснения метода, обозначим на схеме узлы а и б. При обычном расчете это можно не делать.

Далее осуществляем последовательно эквивалентное преобразование схемы. Вначале объединяем параллельно соединенные элементы, и находим:

Затем, объединяя все последовательно соединенные элементы, завершаем эквивалентное преобразование схемы (рис. 1.15, в):

В последней схеме находим ток I₁:

Теперь возвращаемся к предыдущей схеме . Видим, что найдCенный ток I₁ протекает через R₁, R_2,3, R₄ и создает на них падение напряжения. Найдем эти напряжения:.Возвращаясь к исходной схеме , видим, что найденное напряжениеU_аб прикладывается к элементам R₂ и R₃.

Значит, можем записать, чтоU₂ = U₃ = U_а,б

Токи в этих элементах находят из совершенно очевидных соотношений:

Итак, схема рассчитана.