Расчет методом эквивалентного источника напряжения

Этот метод расчета иногда называют методом эквивалентного генератора. Он применяется в тех случаях, когда необходимо определить ток только в одной ветви схемы. Токи в остальных ветвях не представляют интереса. Так, при эксплуатации какого–либо устройства нас интересует часто, какой ток (мощность) будет в нагрузке и (или) какой ток (мощность) будет на входе этого устройства. Известно, что при уменьшении требований к количеству определяемых величин упрощается и сам расчет.

Расчет методом эквивалентного источника напряжения основывается на теореме об эквивалентном источнике напряжения:

"Ток в любой ветви линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником напряжения. ЭДС этого источника должна быть равна напряжению на зажимах разомкнутой ветви, а внутреннее сопротивление источника должно равняться входному сопротивлению пассивной электрической цепи со стороны зажимов подключения ветви при разомкнутой ветви".

Опуская доказательство теоремы (желающим ознакомиться с доказательством рекомендуем [1, стр.95]), рассмотрим последовательность расчета на основании этой теоремы. Исходная схема представлена на рис. 1.19, а.

Здесь выделена только интересующая часть схемы – ветвь а–б, а остальная часть представлена активным двухполюсником А с клеммами а–б. Отсоединяем интересующую нас ветвь а–б (рис. 1.19, б) и, осуществляя расчет оставшейся цепи (двухполюсник А), находим напряжение U_аб на клеммах а–б. Затем в этой же оставшейся схеме (двухполюсник А) (рис. 1.19, б) убираем источники ЭДС, заменяя их на резисторы, сопротивления которых равны внутренним сопротивлениям этих источников или перемычками, если источники идеальны и определяем сопротивление цепи относительно клемм а–б, которое обозначаем через R₀. Величина R₀ определяется методом эквивалентного преобразования. Затем эта часть схемы (двухполюсник А) (рис. 1.19, б) заменяется последовательно соединенными источником ЭДС с нулевым внутренним сопротивлением и ЭДС, равной найденному U_а,б , и резистором с сопротивлением, равным R_0, а к клеммам а–б подключается интересующая ветвь (рис. 1.19, в). Ток в интересующей цепи определяется из очевидного соотношения:

.

Последовательность расчета:

1. Отсоединить от схемы интересующую ветвь, клеммы подсоединения которой обозначить через а–б.

2. Рассчитать оставшуюся часть цепи и определить напряжение на клеммах а–б (U_аб).

3. В оставшейся части цепи заменить источники ЭДС перемычкой или резистором, сопротивление которого равно внутреннему сопротивлению источника ЭДС.

4. Определить сопротивление этой цепи относительно клемм а–б, которое обозначим R₀.

5. Оставшуюся часть цепи заменить последовательно соединёнными источником ЭДС с напряжением U_аб и резистором с сопротивлением R₀. Эту цепь подсоединить к клеммам а–б.

6. К клеммам а–б подсоединить интересующую ветвь и определить ток, протекающий через нее.

Определим ток в ветви а–б схемы (рис. 1.20, а) методом эквивалентного источника напряжения.

Отключаем ветвь а–б (рис. 1.20, б) и находим напряжение на клеммах а–б:

.

Далее исключаем у оставшейся схемы источник E, заменяя его перемычкой, считая, что его внутреннее сопротивление равно нулю (рис. 1.20, в) и определяем сопротивление цепи относительно клемм а–б:

.

Теперь составляем схему (рис. 1.20, г) и находим ток в ветви а–б:

.

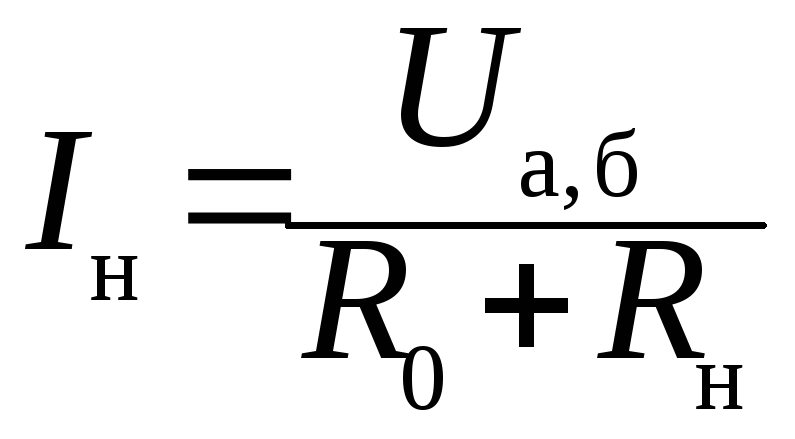На этом расчет закончен.