Виды соединения электрических элементов

Последовательное соединение – такое соединение элементов, при котором в них протекает один и тот же ток. На рис. 1.10 только два резистора соединены последовательно, это резисторы R₃ и R₄.

Параллельное соединение – такое соединение элементов, к которым прикладывается одно и то же напряжение. На рис. 1.10 только два резистора соединены параллельно, это резисторы R₈ и R₉.

Соединение звездой – такое соединение, когда из узла выходит три и более ветви с элементами. Звезда может состоять из трех и более лучей, содержащих элементы. На рис. 1.10 соединение звездой образуют такие, например, элементы: R₅–R₆–R₇, R₁–R₂–R₅ и т. д.

Рис. 1.10. Схема типовых видов соединения элементов

Соединение треугольником – такое соединение, при котором три ветви образуют замкнутый контур. Например, на схеме рис. 1.10 треугольником соединены резисторы R₆–R₇–R₈.

Эквивалентные преобразования подразумевают замену двух и более элементов цепи одним таким элементом, при котором электрические режимы всех оставшихся других элементов не изменяются, т. е. токи и напряжения на этих элементах остаются прежними.

Последовательно соединенные резисторы можно заменить одним резистором, сопротивление которого равно сумме сопротивлений этих резисторов. Так, для схемы, изображенной на рис. 1.11, а имеем:

Рис. 1.11. Эквивалентные преобразования при последовательном (а) и при параллельном (б) соединении элементов

Если последовательно соединены n различных резисторов, то их эквивалентное сопротивление равно:

.

В частном случае, если n последовательно соединенных резисторов имеют одно и то же значение сопротивления R, то их эквивалентное сопротивление в n раз больше этой величины сопротивления и равно:

R_экв = nR.

Очевидно, что величина эквивалентного сопротивления больше наибольшего из последовательно соединённых резисторов.

Параллельно соединенные резисторы можно заменить одним резистором, проводимость которого равна сумме проводимостей каждого из резисторов.

Под проводимостью резистора понимается величина, обратная сопротивлению резистора и обозначается через Y:

.

Для схемы, приведенной на рис. 1.11, б имеем:.

Выражаем проводимости через сопротивления:

.

Решая это выражение относительно R_экв находим:

.

Для n параллельно соединенных резисторов имеем выражения:

; .

О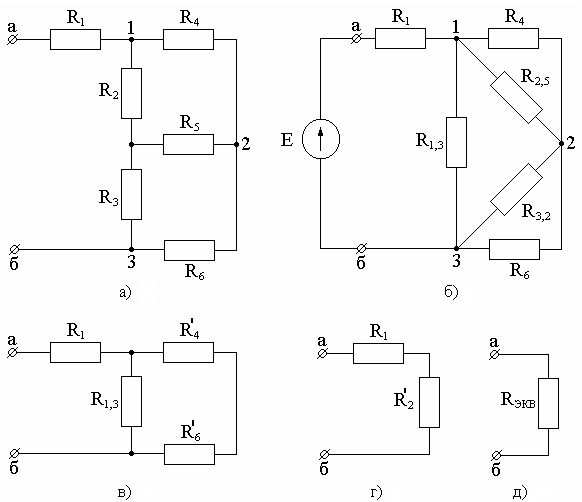тметим несколько особенностей для параллельно соединенных резисторов. Как видно, при параллельном соединении резисторов эквивалентная проводимость больше проводимости резистора, имеющего наибольшее значение проводимости среди всех резисторов. Очевидно, что этот резистор имеет наименьшую величину сопротивления из всех резисторов. Следовательно, эквивалентное сопротивление параллельно соединенных резисторов меньше наименьшего сопротивления из всех резисторов. Это позволяет сделать вывод, что параллельное подключение резистора к какой–либо цепи уменьшает общее (эквивалентное) сопротивление этой цепи.

Если параллельно соединены n резисторов с одинаковым сопротивлением R, то их эквивалентное сопротивление равно:

;

Значит, эквивалентное сопротивление такой цепи в n раз меньше каждого из резисторов.

Соединение звездой и треугольником. Отдельные схемы не возможно эквивалентно преобразовать и найти их полное сопротивление относительно входных выводов, если не осуществить переход от соединения электрических элементов звездой к соединению их треугольником или на оборот. При замене звезды (рис. 1.12, а) на эквивалентный треугольник (рис. 1.12, б) сопротивления треугольника связаны с сопротивлениями звезды следующими соотношениями:

При замене треугольника на эквивалентную звезду сопротивление звезды выражается через сопротивление треугольника следующими соотношениями:

; ;.

На рис. 1.13 показана последовательность эквивалентного преобразования цепи для определения эквивалентного сопротивления всей цепи относительно точек а–б. Обычно преобразование начинается с объединения последовательно или параллельно соединенных элементов. В исходной схеме (рис. 1.13, а) таких соединений нет. В этом случае необходимо выполнить преобразование звезды в треугольник или треугольника в звезду. В исходной схеме звезду из резисторов R₂–R₅–R₃ заменяем треугольником (рис. 1.13, б) из резисторов R_1,3, R_2,5, R_3,2, величины которых находятся из выше приведенных формул. Теперь видно, что резисторы R₄ и R_2,5, а также резисторы R₆ и R_3,2 соединены между собой параллельно и объединяются соответственно в резисторы R'₄, R'₆ (рис. 1.13, в). Затем объединяются последовательно соединенные резисторы R'₄ и R'₆ с параллельно с ними соединенным резистором R_1,3. Их эквивалентом является резистор R'₂ (рис. 1.13, г). Суммируя R₁ и R'₂, находим R_экв для всей цепи (рис. 1.13, д).