Тема 7. Исследование поведения функции

Задача 18. Исследовать функцию и построить ее график.

Решение:

1. Определим область существования функции. Квадратный трехчлен, стоящий под знаком логарифма, можно представить так: . Как видно, под знаком логарифма будет положительное число при любом значении аргументах. Следовательно, областью существования данной функции служит вся числовая ось.

2. Исследуем функцию на непрерывность. Функция всюду непрерывна и не имеет точек разрыва.

3. Установим четность и нечетность функции. Так как и то функция не является ни четной, ни нечетной.

4. Исследуем функцию на экстремум. Находим первую производную:

Знаменатель для любого значениях. Как видно, при первая производная отрицательна, а приположительна. Прих = 3 первая производная меняет свой знак с минуса на плюс. В этой точке функция имеет минимум:

Итак, А(3; 0) — точка минимума (см. рис. 8). Функция убывает на интервале и возрастает на интервале.

5. Определим точки перегиба графика функции и интервалы выпуклости и вогнутости кривой. Для этого находим вторую производную:

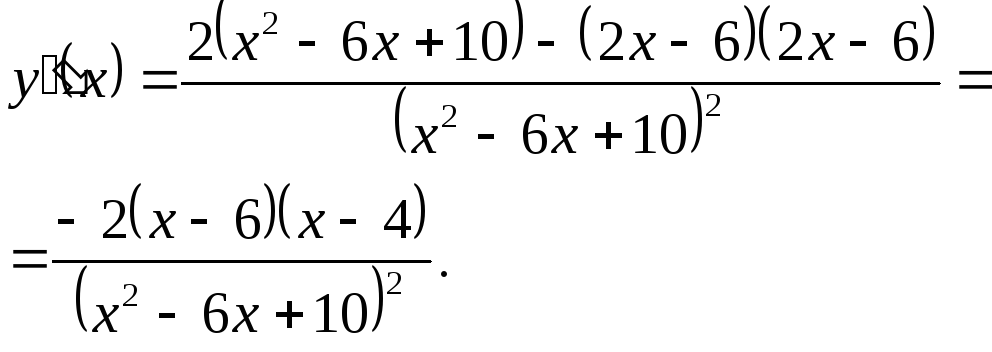
Разобьем всю числовую ось на три интервала:Как видно, в первом и третьем интервалах вторая производная отрицательна, а во втором интервале положительна. Прих₁ = 2 и х₂ = 4 вторая производная меняет свой знак. Эти значения аргумента являются абсциссами точек перегиба. Определим ординаты точек:

Следовательно, и— точки перегиба графика функции. График является выпуклым в интервалахи, и вогнутым в интервале(2, 4).

6. Определим уравнения асимптот графика функции. Для определения уравнения невертикальной асимптоты воспользуемся формулами:

Имеем

Чтобы найти искомый предел, дважды применяем правило Лопиталя:

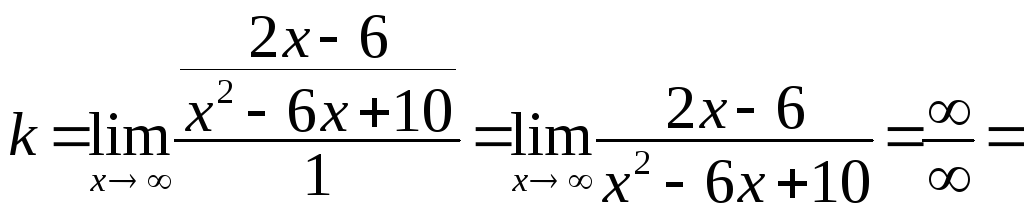
Итак, кривая не имеет асимптот. График исследуемой функции показан на рис. 8.

Задача 19. Исследовать функцию и построить ее график.

Решение: 1. Функция терпит разрыв при х=2. При всех других значениях аргумента она непрерывна.

2. Функция не является ни четной, ни нечетной, так как и

3.Исследуем функцию на экстремум, используя вто­рой достаточный признак экстремума: если в стационарной точке х₀ вторая производная отлична от нуля, то в этой точке функция имеет максимум прии минимум приНаходим первую производную:

(1)

или

Как видно, первая производная равна нулю при х = 1 и х = 3 и не существует при х = 2. Так как при х = 2 заданная функция не существует, то эта точка не подлежит исследованию. Дифференцируя (1), находим вторую производную у":

Сократив на и выполнив преобразования в числителе, получим

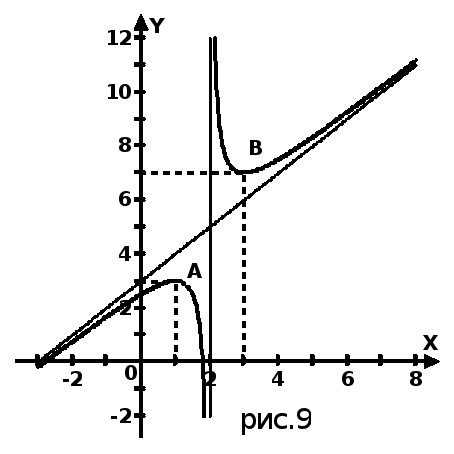(2)

Так как то прих₁ = 1 функция имеет максимум. Так как то прих₂ = 3 функция имеет минимум.

Вычислим значения функции в точках экстремума: y(1) = 3; у (3) = 7. Следовательно, А (1; 3) — точка максимума, В(3; 7) — точка минимума.

4. Из (2) видно, что вторая производная ни при каком значении аргумента не обращается в ноль. Следовательно, график исследуемой функции не имеет точек перегиба.

5. Определим асимптоты графика функции, х = 2 есть уравнение вертикальной асимптоты. Используя соответствующие формулы, выясним вопрос о наличии наклонной асимптоты:

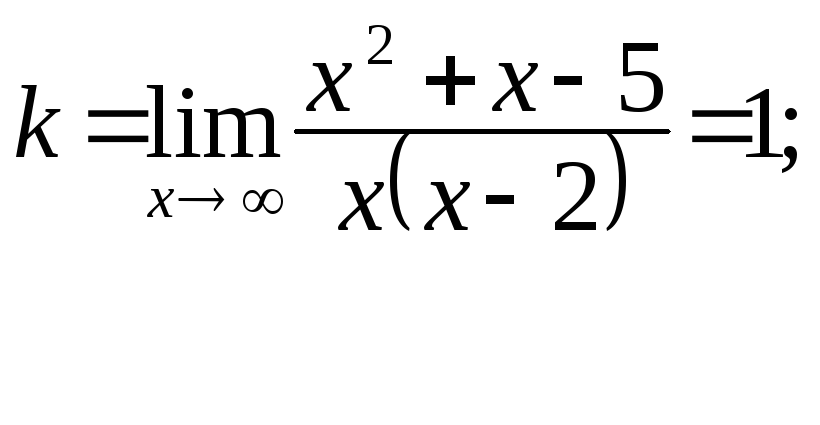
Следовательно, – уравнение наклонной асимптоты. График исследуемой функции приведен на рис. 9.

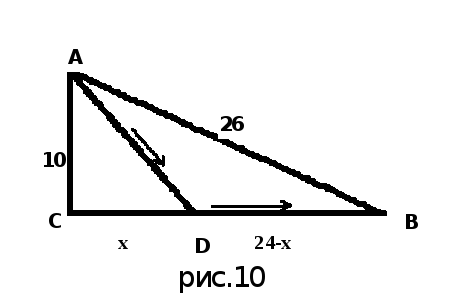
Задача 20. Расстояние от центральной усадьбы совхоза до районного центра, расположенного у асфальтированной прямолинейной дороги, составляет 26 км (отрезок АВ на рис. 10), а кратчайшее расстояние от центральной усадьбы до этой дороги — 10 км (отрезок АС). Скорость велосипедиста на асфальтированной дороге равна 20 км/ч, а за ее пределами — 12 км/ч. Найти минимальное время, в течение которого велосипедист преодолеет путь от центральной усадьбы до районного центра.

Решение: Пусть CD = х, тогда Путь велосипедиста состоит из двух участков AD и BD. На первом участке его скорость равна 12 км/ч, на втором — 20 км/ч. Время, затраченное велосипедистом на весь путь,

(1)

(Из прямоугольного треугольника АВС следует, что ВС = 24; следовательно, BD = 24 —х.)

Исследуем функцию (1) на экстремум. Найдем первую производную, приравняем ее нулю и решим полученное уравнение. Имеем

(2)

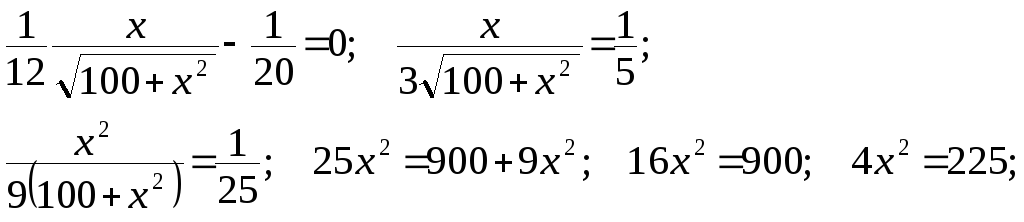
откуда

Определим знак производной (2) при и при

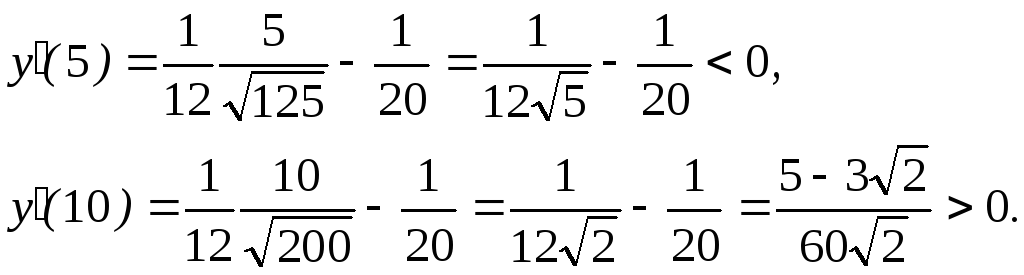
При х = 7,5 производная изменяет знак с минуса на плюс; значит, при этом значении аргумента функция имеет минимум. Подставив в (1) х = 7,5, получим

Таким образом, минимальное время нахождения в пути велосипедиста составляет 1 ч 52 мин.

Заметим, что при x = 0, т.е. если выбрать кратчайший путь до асфальтированной дороги, а затем двигаться по ней, то время в пути составит у(0) = 2 ч 02 мин. Если же выбрать прямой путь по неасфальтированной дороге (т.е. при х = 24), то время в пути составит 2 ч 10 мин.