разное к тоэ / Rgr4 / РГР04(Перекрестов)(16)

Расчетно-графическая работа №4.

Переходные процессы в линейных электрических цепях.

Задача 1. (на применение классического и операторных методов) Дана электрическая цепь, в которой происходит коммутация (рис 1). В цепи действует постоянная ЭДС Е. Параметры цепи приведены в таблице 1. Требуется определить закон изменения во времени тока после коммутации в одной из ветвей схемы или напряжения, на каком либо элементе или между заданными точками схемы.

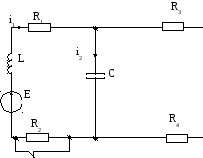
Схема 1.

Таблица 1.

Данные для задачи №1.

Е, В	L, мГн	С, мкФ	R1	R2	R3	R4	Определить
50	2	1670	1	2	1	5	i1

1,1 Решим задачу классическим методом.

1,1,1 Найдем ток через индуктивность и напряжение на конденсаторе в цепи до коммутации.

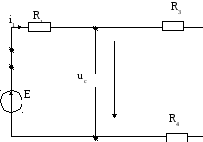
Схема 2.

Здесь мы учли, что катушка дает закоротку, а конденсатор разрыв.

Для определения u_c(0-) и i_L(0-) воспользуемся методами расчета для цепей постоянного тока.

Тогда ток I₁ будет равен.

следовательно, падение напряжения на конденсаторе будет равно:

u_c(0-)= i₁* (R₃+R₄)=37,5 (В)

применяя 1 и 2 законы коммутации, запишем токи через индуктивность и напряжения на емкостях непосредственно после коммутации.

u_c(0+)= u_c(0-)=37,5 (В)

i_L(0+)= i_L(0-)=6,25 (А)

1,1,2. Определим принужденные составляющие тока через индуктивность и напряжения на конденсаторе, а также принужденное значение расчетной величины в цепи после коммутации.

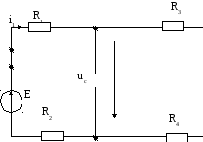
Схема 3.

По закону Ома для участка цепи.

подставляя численные значения, получим.

1,1,3. Определим свободные составляющие тока через индуктивность и напряжения на конденсаторе.

1,1,4. Составим характеристическое уравнение путем определения входного сопротивления схемы «Z». При этом источник ЭДС закорачивается, схема разрывается в любом месте и относительно точек разрыва определяется сопротивление.

R₁

R₃

Lp

1 Ср

Z(p)

R₂

R₄

Схема 4.

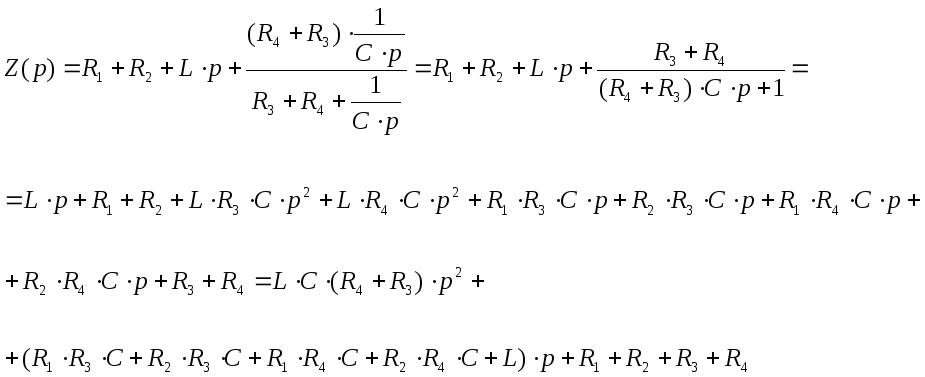
подставим численные значения сопротивлений, емкости и индуктивности, а затем полученное выражение приравняем к 0. это и будет характеристическое уравнение.

решим получившееся квадратное уравнение

1,1,5. У нас получилось два отрицательных не равных между собой действительных корня. Тогда решение для свободной составляющей искомой величины запишется в виде следующего выражения.

1,1,6. Для определения коэффициентов А₁ и А₂, составляется система уравнений включающая решение и производную до n-1 порядка включительно. У нас два корня, значит нам нужно найти производную первого порядка.

для момента времени t=0.

(*)

так как нам не известна, то для ее нахождения составим систему уравнений по 1 и 2 законам Кирхгофа для свободный составляющих и производных от этих уравнений до n-1 порядка включительно.

i_{2 св}(t)

i_{1 св}(t)

R₁

R₃

L

i_{3 св}(t)

u_{с св}(t)

C

R₄

R₂

Схема 5.

Запишем 6 уравнений для момента времени t=0.

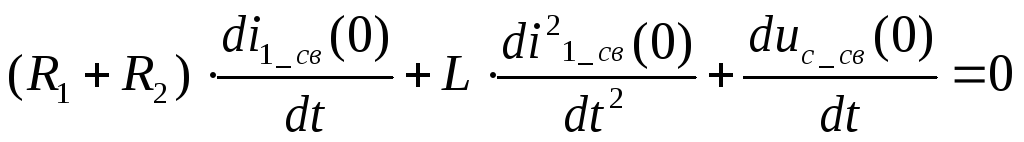
из уравнения 1 данной системы получим, что:

подставляя известные числовые значения, получим.

1,1,8. решим систему (*) относительно неизвестных коэффициентов А.

1,1,9. запишем решение для свободной составляющей искомой величины в соответствии с пунктом 1,1,5.

1,1,10. Общее решение искомой величины запишется в виде.

1,2. Решим ту же задачу операторным методом.

1,2,1. Найдем ток через индуктивность и напряжение на конденсаторе в цепи до коммутации.

Так как условие задачи не изменилось то эти данные можно взять из решения задачи классическим методом (см. выше пункт 1,1,1).

u_c(0+)= u_c(0-)=37,5 (В)

i_L(0+)= i_L(0-)=6,25 (А)

1,2,2. Составим операторную схему замещения для послекоммутационной схемы.

I₁ (p)

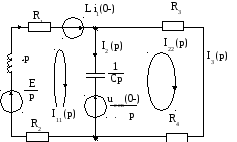
Схема 6.

Рассчитаем эту схему, используя метод контурных токов. Составим систему уравнений.

Так как нам необходимо рассчитать только ток I₁(p), который равен:

I₁(p)=I₁₁(p)=

то нам необходимо вычислить еще только один определитель, а именно Δ₁.

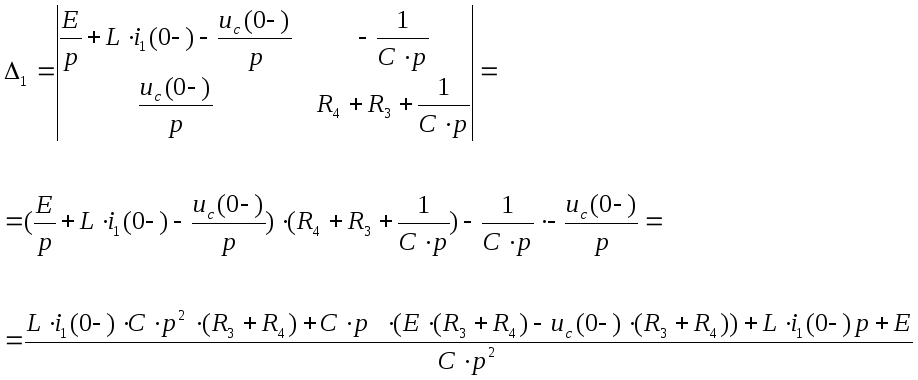
тогда ток I₁(p) будет равен

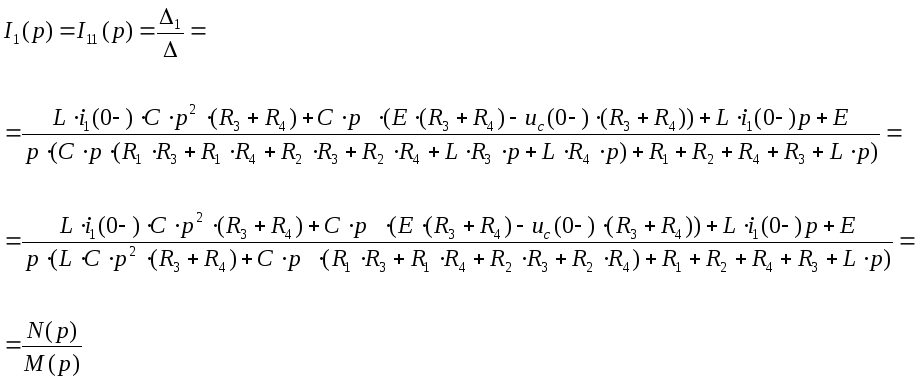
1,2,3. перейдем от изображения к оригиналу. Для осуществления перехода найдем корни характеристического уравнения.

M(p)=0

р₀=0

решим получившееся квадратное уравнение

при трех корнях переход осуществляется так.

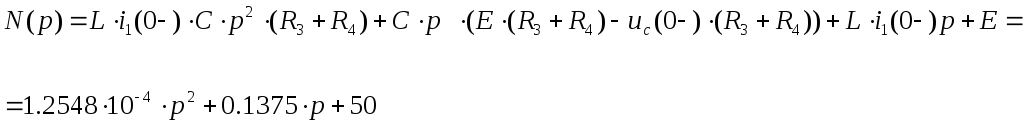
тогда ток i₁(t) будет равен.

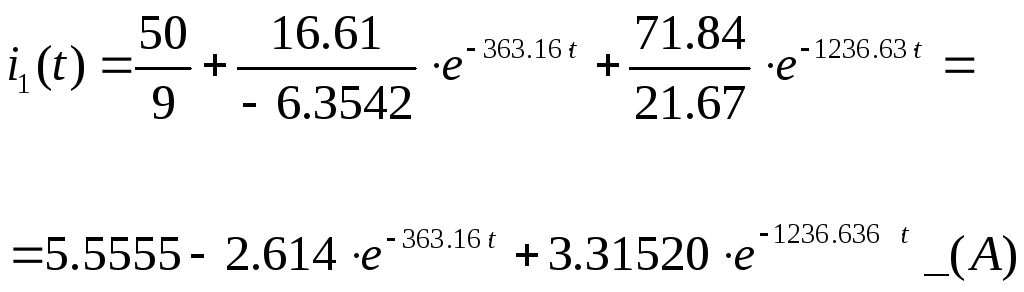
1,3. на основании полученного выражения построим график изменения искомой величины, тока i₁(t) в функции времени на интервале от t=0 до t=3/363.16 (меньший по модулю корень характеристического уравнения)

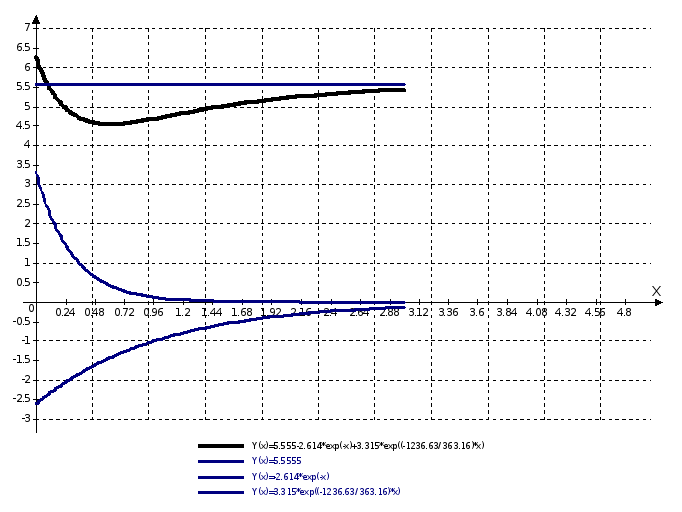
График 1.

Результаты, полученные классическим и операторным методами совпадают. Значит расчеты сделаны верно.

Задача 2,. Дана электрическая схема (схема 7), на входе которой действует напряжение, изменяющееся во времени по заданному закону u₁(t). Требуется определить закон изменения во времени тока в одной из ветвей схемы или напряжения на заданном участке схемы. В таблице 3 в соответствии с номером варианта указан номер рисунка, на котором приведен график изменения во времени входного напряжения. Параметры цепи R, L, C заданы в буквенном виде.

Задачу требуется решить с помощью интеграла Дюамеля. Искомую величину следует определить (записать ее аналитическое выражение) для всех интервалов времени. В зависимости от условий задачи полный ответ будет содержать два или три соотношения, каждое из которых справедливо лишь в определенных границах изменения времени t.

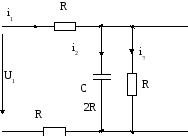
Схема 7.

Таблица 3.

Данные для задания №2

Вариант	Рисунок	График	Определить
16	7	2	i2

u₁

U₁=A+kt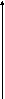

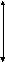
2 A

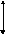
A

t

0

t₁

t₂

График 2.

Решение проведем операторным методом.

2,1. На вход нашей схемы подадим испытательную функцию Хевисайда:

С

R

оставим операторную схему замещения при нулевых начальных условиях.

I₂(p)

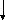
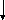
I₃(p)

I₁(p)

1 р

1 С р

R

R

Схема 8.

Нам необходимо определить I₂(p). Для расчета этого значения напряжения воспользуемся методом контурных токов.

Составим систему уравнений.

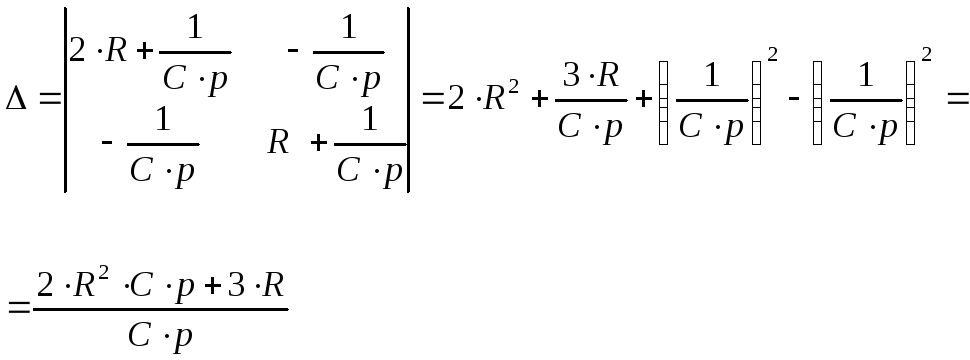
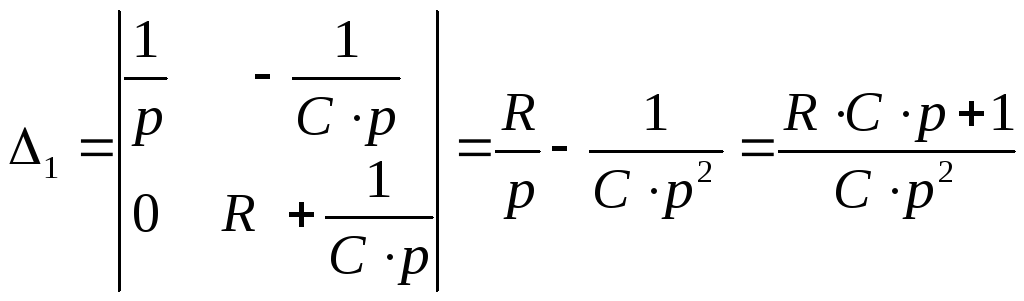
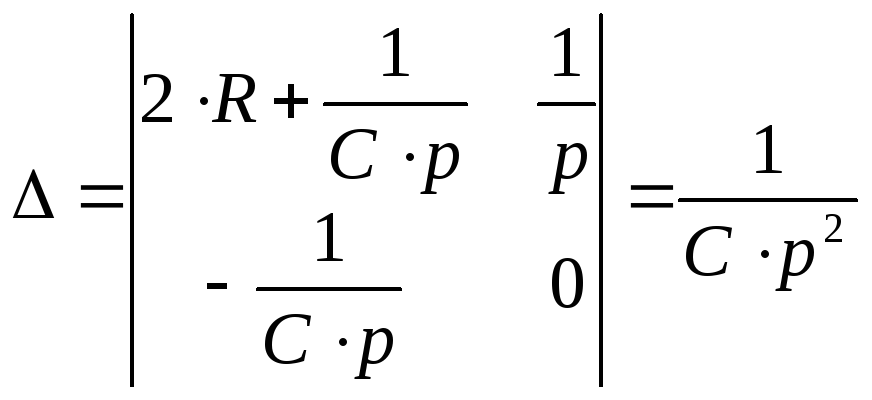
тогда ток I₂(p) будет равен

перейдем от изображения к оригиналу. Для осуществления перехода найдем корни характеристического уравнения.

M(p)=0

при одном корне переход осуществляется так.

тогда ток i₂(t) будет равен.

Переходная функция по току численно равна напряжению u_c при единичном входном воздействии.

Запишем интеграл Дюамеля для каждого интервала времени в отдельности.

Для (0, t₁).

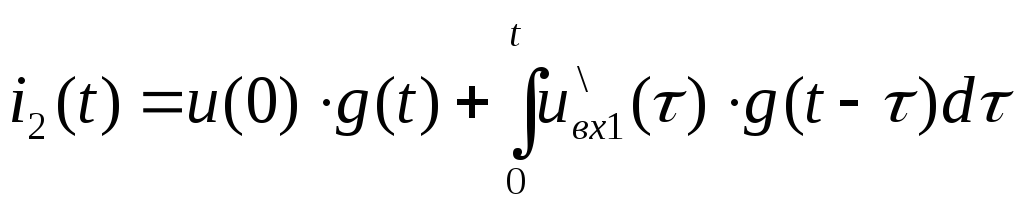
Подставим эти значения в наш интеграл и вычислим его.

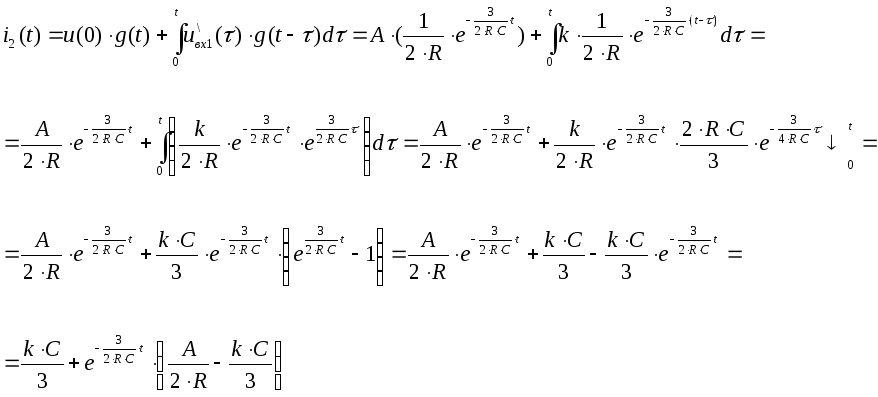
Для ( t₁, t₂ ).

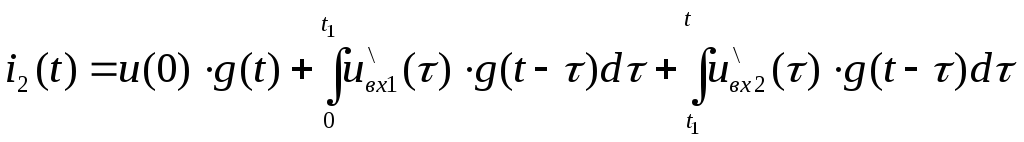
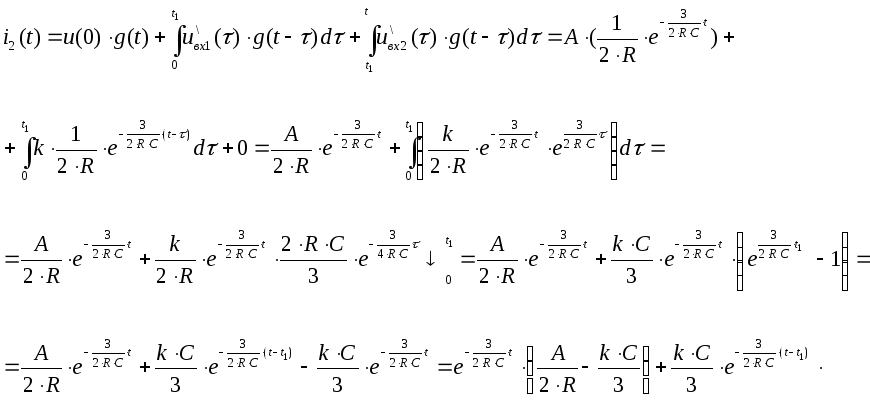
Для ( t₁, +οο).

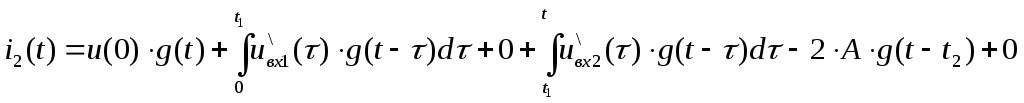
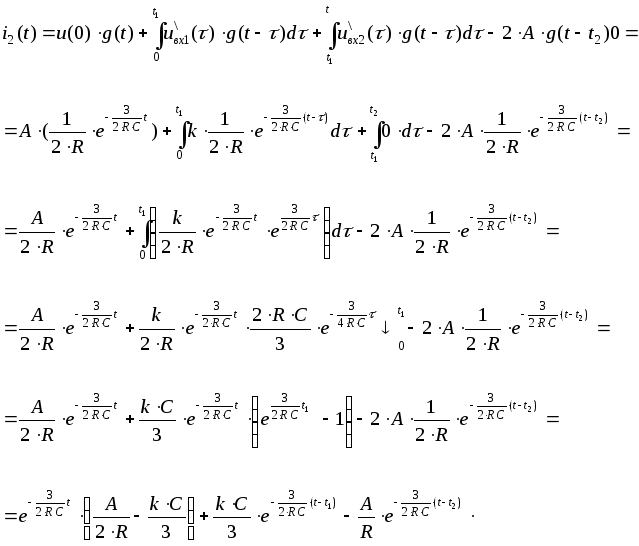
То есть у нас в ответе получилось 3 соотношения, каждое из которых справедливо лишь в определенных границах изменения t.

Задача 3. Для каждого варианта в таблице 4 указан номер рисунка. нa котором качественно изображен импульс напряжения u(t), а также записано аналитическое выражение импульса Входящие в него параметры указаны в таблице 4 Требуется:

1 Получить аналитическое выражение для модуля и аргумента cпектра этой функции.

2 Полученное выражение |U(jω) | представить в функции безразмерной величины ω/α.

3 Построить зависимость |U(jω) | в функции ω/α.

Таблица 4.

Данные для задания №3

α, 1/с	β, 1/с	К	t, с	U, В
50	---	---	---	100

u₁

A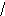

t

0

График 3.

1,. По условию нам задана следующая функция:

по таблице соответствия между оригиналом и изображением, найдем изображение искомой функции.

заменим р на jω.

Найдем модуль функции.

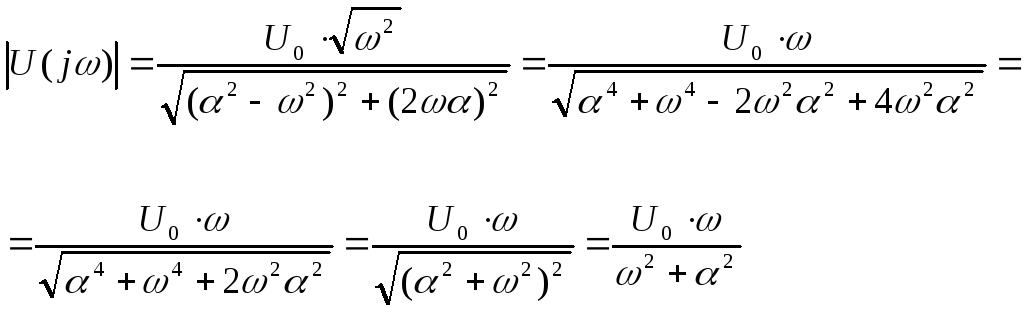
Представим в показательной форме.

где.

Разделим числитель и знаменатель на α².

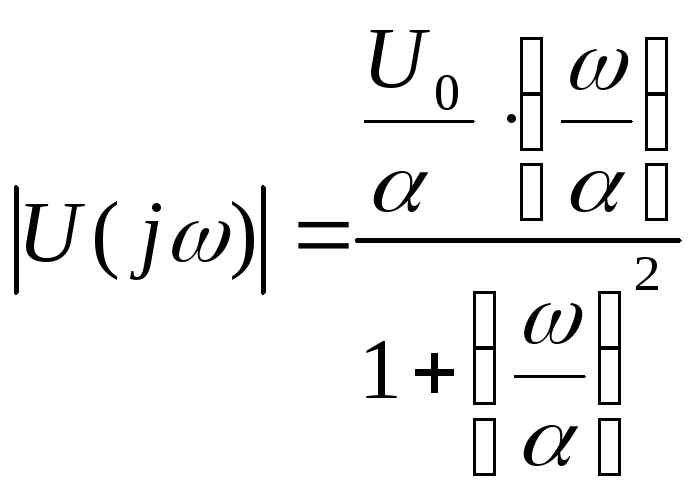
для построения модуля функции в относительных единицах проведем дополнительные преобразования.