3.2.6 Расчёт нормального сечения на трещиностойкость

Проверка нормального сечения на раскрытие трещин:

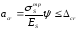(3.69)

где максимальные напряжения, возникающие в арматуре при расчёте на трещиностойкость.

(3.70)

- коэффициент раскрытия трещин для стержневой арматуры периодического профиля:

где - радиус армирования;

–площадь зоны взаимодействия для нормального сечения (зона взаимодействия ограничивается горизонтальной линией, проводимой на расстоянии радиуса взаимодействия, равного 6d, от ближайшего к ней ряда стержней).

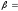0,75; 30;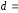0,04 м.

0,005< 0,02 - условие выполняется

На образование продольных трещин:

Проверку производим по формуле:

(3.71)

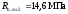(для бетона класса В30)

9,91 < 14,6 - условие выполняется.

3.2.7 Определение прогиба балки в середине пролета от нормативной временной вертикальной нагрузки

Должно выполняться условие:

; (3.72)

где - предельная величина прогиба в середине пролета

; (3.73)

где - модуль упругости бетона, по п 7.32 [1]

 = 0,85 – коэффициент, исключающий тяжелые транспортеры

м

м

Условие выполняется.

3.2.8 Построение эпюры материалов с отметкой отгибов рабочей арматуры

Для определения мест отгибов рабочей арматуры необходимо построить огибающую эпюру максимальных моментов в балке.

Начало отгибов продольных растянутых стержней арматуры расположено за сечением, в котором стержни учитываются с полным расчетным сопротивлением. Длина заводки за сечение для арматуры стали класса А300 и класса бетона В30 определена по формуле:

, (3.74)

Из формулы (3.84) рассчитано:

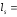22 ∙ 0,04 = 0,88 м.

При построении эпюры материалов использованы конструктивные требования СП 35.13330.2011.

3.2.9 Расчёт на прочность наклонных сечений главной балки.

Для железобетонных элементов должно быть соблюдено условие, обеспечивающее прочность по сжатому бетону между наклонными трещинами:

(3.75)

где: - поперечная сила на расстоянии не ближеот оси опоры;

- рабочая высота сечения;

(3.76)

где: - при хомутах, нормальных к продольной оси;

- отношение модулей упругости арматуры и бетона;

- площадь сечения ветвей хомутов, расположенных в одной плоскости;

- расстояние между хомутами по нормали к ним.

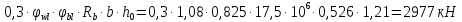
Расчет наклонного сечения на действие поперечной силы произведем из условия:

(3.77)

где: - сумма проекций усилий всей пересекаемой наклонной к оси элемента арматуры на длине проекциис, не превышающей;

- угол между отогнутой арматурой и наклонным сечением (90°);

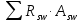- сумма проекций усилий всей пересекаемой нормальной к оси элемента арматуры на длине проекции с, не превышающей;

- поперечное усилие, передаваемое на бетон сжатой зоны над концом наклонного сечения:

(3.78)

Рисунок 2.9 - Схема для расчета наклонного сечения

Условие выполняется.

Расчет наклонного сечения на действие поперечной силы производится из условия:

_, (3.69)

_где 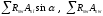– суммы проекций усилий всей пересекаемой арматуры

R_sw=0,8·250=200 МПа;

А_s=0,001257м²

_{Qwr– поперечная сила, воспринимаемая продольной арматурой:}

где A_s^r– площадь горизонтальной арматуры, пересекаемой наклонным сечением.

–коэффициент;

β=45˚– угол между продольной арматурой и сечением.

Так как k<0, принимаемk =0;0.

Q_b– поперечное усилие, передаваемое на бетон сжатой зоны над концом наклонного сечения, определяемое по формуле:

_,

Условие выполняется.

_{Прочность по сжатому бетону между наклонными трещинами:}

, (3.70)

где Q - поперечная сила на расстоянии не ближе h₀от оси опоры;

= 1 + ηn₁A_sw/(bS_w), при расположении хомутов нормально к продольной оси

≤1,3;

η =5 – при хомутах, нормальных к оси элемента;

–отношение модулей упругости арматуры и бетона

A_sw=0,078·10^-3м²– площадь сечения ветвей хомутов, расположенных в одной плоскости;

S_w– расстояние между хомутами по нормали к ним, S_w=0,15м;

_b=0,26 - толщина стенки главной балки

= 1 – 0,01R_b– коэффициент. Здесь R_bпринимаем в МПа,

–рабочая высота сечения, =1,2 м.

==1,06

=1-0,01·15,5=0,845;

=2998,8 кН

Q=1869,30 кН;

1869,30<2998,8 (кН)

Условие выполняется.

Расчет наклонного сечения на действие поперечной силы производится из условия:

(3.85)

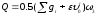(3.86)

_где – суммы проекций усилий всей пересекаемой арматуры на длине проекцииc=h₀;R_sw=0,8·250=200МПа;

Q_b– поперечное усилие, передаваемое на бетон сжатой зоны над концом наклонного сечения, определяемое по формуле:

_{, m=2.}

_{Qwr– поперечная сила, воспринимаемая продольной арматурой:}

где A_s^r– площадь горизонтальной арматуры, пересекаемой наклонным сечением.

–коэффициент; β – угол между продольной арматурой и сечением.

Так как k<0, принимаемk =0;0.

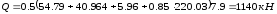
Условие выполняется.

_{Прочность по сжатому бетону между наклонными трещинами:}

, (2.51)

где Q - поперечная сила на расстоянии не ближе h₀от оси опоры;

= 1 + ηn₁A_sw/(bS_w), при расположении хомутов нормально к продольной оси≤1,3;

η =5 – при хомутах, нормальных к оси элемента;

n₁– отношение модулей упругости арматуры и бетона (п. 3.48 [2]),

A_sw – площадь сечения ветвей хомутов, расположенных в одной плоскости;

S_w– расстояние между хомутами по нормали к ним,S_w=0,15м;

- толщина стенки (ребра) главной балки b=0,5;

= 1 – 0,01R_b– коэффициент. Здесь R_bпринимаем в МПа,

–рабочая высота сечения, =1,31 м.

_Asw=18*0,008²*3,14/4=0,0009 м²;

==1,432

_{должен быть не более 1,3, принимаем}

=1-0,01·11.75=0,88;

=8804 кН

Q = 1140 кН.

1140<8804

Условие выполняется.

Рисунок 3.9 – Отгибы рабочей арматуры

Рисунок 3.10 – Эпюра материалов и отгибы рабочей арматуры