2. Решение систем дифференциальных уравнений численными методами в среде MathCad

Метод Рунге-Кутта

Решим методом Рунге-Кутта исходную систему дифференциальных уравнений, записанную в виде:

для следующих начальных условий:

_,

_{Присвоим начальному индексу массивов значение 1.}

_{Сформируем вектор правых частей системы дифференциальных уравнений:}

_{Сформируем вектор начальных условий:}

_{Вызов функции rkfixed():}

_{Результат работы функции – матрица Xrk (таблица) значений, первый столбец которой содержит значения времени, второй искомые значения x1(t), третий – x2(t).}

Для построения графика функций предварительно зададим интервал изменения индекса:

Рис. 3.2. Сравнение численного решения методом Рунге-Кутта (штрихи) и аналитического (сплошные линии) решения системы дифференциальных уравнений

Метод Рунге-Куттас адаптивным шагом

Решим ту же систему дифференциальных уравнений методом Рунге-Кутта с адаптивным шагом.

Вектор правых частей уравнения и вектор начальных условий уже сформированы выше в примере решения системы дифференциальных уравнений методом Рунге-Кутта

_{Вызов функции rkadapt():}

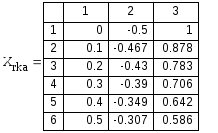
_{Результат работы функции – матрица Xrkа (таблица) значений, первый столбец которой содержит значения времени, второй искомые значения x1(t), третий – x2(t).}

Для построения графика функций предварительно зададим интервал изменения индекса:

Рис. 3.3. Сравнение численного решения методом Рунге-Кутта с адаптивным шагом (штрихи) и аналитического (сплошные линии) решения системы дифференциальных уравнений

Метод Булирша-Штера

Решим ту же систему дифференциальных уравнений методом Булирша-Штера. Вектор правых частей уравнения и вектор начальных условий уже сформированы выше в примере решения системы дифференциальных уравнений методом Рунге-Кутта

_{Вызов функции Bulstoer():}

_{Результат работы функции – матрица Xrkb (таблица) значений, первый столбец которой содержит значения времени, второй искомые значения x1(t), третий – x2(t).}

Для построения графика функций предварительно зададим интервал изменения индекса:

Рис. 3.4. Сравнение численного решения методом Булирша-Штера(штрихи) и аналитического (сплошные линии) решения системы дифференциальных уравнений

3. Приведение дифференциальных уравнений высших порядков к нормальному виду

Приведем дифференциальное уравнение к системе нормальных дифференциальных уравнений:

.

Введем замену:

x(t)=x₁(t),

_,

.

тогда

_,

.

Приводим к нормальному виду:

_,

.

В матричном виде система уравнений (44):

или

.

4. Приведение матричного уравнения к новым координатам

Решим полученное в предыдущем пункте уравнение с помощью MathCad. Задаем исходные данные:

Решение будем искать в виде:

Так как матрица А недиагональная, то решение будем искать с помощью приведения системы дифференциальных уравнений к новым координатам. Для этого определяем собственные значения матрицы А – векторlи формируем матрицуL:

находим матрицу L, обратнуюT, а затем и матрицуТ:

Выполняем проверку:

находим значения матрицы и подынтегрального выражения:

Находим функции y(t)иx(t):

Строим график:

Рис. 3.5. Решение с помощью приведения системы дифференциальных уравнений к новым координатам

Контрольные вопросы

1. Представьте дифференциальное уравнение третьего порядка, описывающее систему, в виде системы дифференциальных уравнений первого порядка в нормальном виде.

2. Выведите общий вид аналитического решения дифференциального матричного уравнения.

3. Перечислите функции Mathcadдля численного решения систем дифференциальных уравнений.

4. Как решить дифференциальное уравнение четвертого порядка с помощью функций rkfixed,rkadapt,bulstoer?

5. В чем отличия между функциями rkfixed,rkadapt,bulstoer?

6. Как решить дифференциальное матричное уравнение третьего порядка с помощью диагонализации матриц?