- •26.Интегральная сумма Римана. Определенный интеграл Римана. Интегрируемые
- •Геометрический смысл определенного интеграла
- •27.Определенный интегралРимана. Свойстваопределенногоинтеграла.Теорема о среднем.
- •28.Определенный интеграл с переменнымверхнимпределом. Теорема о егопроизводной.Существованиепервообразной непрерывной функции.
- •Доказательство.
- •Разбиение промежутка интегрирования
- •29.Определенный интеграл с переменнымверхнимпределом. ФормулаНьютона- Лейбница.
- •Доказательство.
- •30.Определенный интеграл Римана. Методы вычисления: интегрирование по частям и замена переменной.
- •Определенные интегралы (интеграл Римана).
- •31.Понятие о несобственныхинтегралах I-города. Интегралывида (a , p 0 ).
- •32.Понятие о несобственныхинтегралах II-города. Интегралывида
- •Несобственные интегралы второго рода
- •Полярная система координат и криволинейный сектор.
- •35.Вычисление объемовтелпоплощадямпоперечныхсечений и объемовтел
- •36.Функции двухпеременных. Передел и непрерывность.Частныепроизводные, их
- •40.Формула Тейлорадляфункциидвухпеременных.
- •41.Экстремумы функциидвухпеременных. Необходимоеусловиесуществования
- •42.Экстремумы функциидвухпеременных. Достаточноеусловиесуществования
- •44.Определение двойногоинтеграла.
- •Что значит вычислить двойной интеграл?
- •50.Вычисление тройногоинтеграла в цилиндрической системекоординат.
- •52.Приложения тройногоинтеграла.
42.Экстремумы функциидвухпеременных. Достаточноеусловиесуществования
экстремума (формулировка).
Пусть
функция 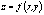 определена
в некоторой области G и точка
определена
в некоторой области G и точка 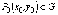 .
.
Функция 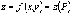 имеет
в точке
имеет
в точке 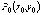 максимум,
если существует такая окрестность этой
точки, что для всех точек
максимум,
если существует такая окрестность этой
точки, что для всех точек 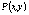 этой
окрестности, отличных от
этой
окрестности, отличных от 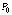 ,
выполняется неравенство
,
выполняется неравенство 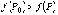 .
.
Аналогично определяется минимум функции.
Максимум и минимум функции называются экстремумами функции.
Теорема (необходимое
условие экстремума). Если 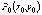 –точка
экстремума функции
–точка
экстремума функции 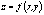 , то
частные производные
, то
частные производные 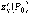 и
и 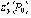 в
этой точке равны нулю или не существуют.
в
этой точке равны нулю или не существуют.
Точки,
в которых частные производные 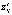 и
и 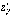 обращаются
в нуль или не существуют,
называются критическими точками
этой функции.
обращаются
в нуль или не существуют,
называются критическими точками
этой функции.
Сформулированный признак не является достаточным: не обязательно критическая точка является точкой экстремума.
Чтобы проверить, есть ли экстремум в критической точке, используют следующую теорему (достаточное условие экстремума).
Пусть
в некоторой области, содержащей
точку 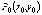 , функция
, функция 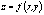 имеет
непрерывные частные производные до
3–го порядка включительно
и
имеет
непрерывные частные производные до
3–го порядка включительно
и 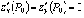 . Обозначим:
. Обозначим:  . Тогда
. Тогда
1)если 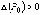 , то
функция имеет экстремум в точке
, то
функция имеет экстремум в точке 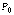 ,
причем это максимум, если
,
причем это максимум, если 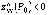 и
минимум, если
и
минимум, если 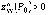 ;
;
2)если 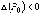 , то
экстремума в точке
, то
экстремума в точке 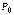 нет;
нет;
3)если 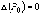 , требуется
дополнительное исследование (экстремум
в точке
, требуется
дополнительное исследование (экстремум
в точке 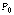 может
быть или не быть).
может
быть или не быть).
Пример.
Исследовать на экстремум функцию 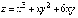 .
.
Решение.
Найдем критические точки функции. 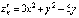 ;
; 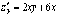 .
Решим систему
.
Решим систему 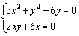 .
Из 2–го уравнения
.
Из 2–го уравнения 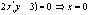 или
или 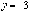 .
Подставив эти значения в 1–ое уравнение,
получим: при
.
Подставив эти значения в 1–ое уравнение,
получим: при 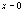
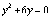 ,
, 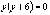 ,
, 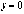 или
или 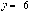 ;
при
;
при 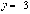 ,
, 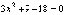 ,
, 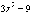 ,
, 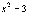 ,
, 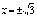 .
Таким образом, функция имеет четыре
критических точки:
.
Таким образом, функция имеет четыре
критических точки: 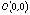 ,
, 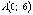 ,
, 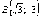 ,
, 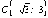 .
Проверим, есть ли экстремум в этих
точках.
.
Проверим, есть ли экстремум в этих
точках.
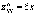 ;
; 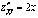 ;
; 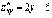 .
.
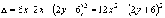 ;
;
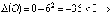 в
точке O экстремума нет.
в
точке O экстремума нет.
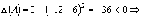 в
точке A экстремума нет.
в
точке A экстремума нет.
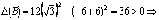 в
точке B экстремум есть, причем
в
точке B экстремум есть, причем 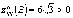 ,
значит, это минимум.
,
значит, это минимум. 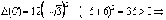 в
точке C экстремум есть, причем
в
точке C экстремум есть, причем 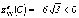 ,
значит, это максимум.
,
значит, это максимум. 
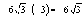 –минимум
функции,
–минимум
функции, 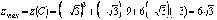 –максимум
функции.
–максимум
функции.
43.Дифференцирование функции, заданной неявно.
21.1. Неявно заданная функция
Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функцию у.
<< Пример 21.1
Найти производную функции у, заданную уравнением х3+у3-3ху=0.
Решение: Функция у задана неявно. Дифференцируем по х равенство х3+у3-3ху=0. Из полученного соотношения
3х2+3у2· у'-3(1· у+х· у')=0
следует, что у2у'-ху'=у-х2, т. е. у'=(у-х2)/(у2-х).
21.2. Функция, заданная параметрически
Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.
Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем
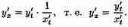
Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х.
<< Пример 21.2
Пусть 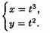
Найти у'х.
Решение:
Имеем x't=3t2,
y't=2t. Следовательно,
у'х=2t/t2, т. е. 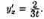
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно, 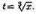 Тогда
Тогда 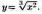 Отсюда
Отсюда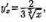 т.
е.
т.
е.