
- •26.Интегральная сумма Римана. Определенный интеграл Римана. Интегрируемые
- •Геометрический смысл определенного интеграла
- •27.Определенный интегралРимана. Свойстваопределенногоинтеграла.Теорема о среднем.
- •28.Определенный интеграл с переменнымверхнимпределом. Теорема о егопроизводной.Существованиепервообразной непрерывной функции.
- •Доказательство.
- •Разбиение промежутка интегрирования
- •29.Определенный интеграл с переменнымверхнимпределом. ФормулаНьютона- Лейбница.
- •Доказательство.
- •30.Определенный интеграл Римана. Методы вычисления: интегрирование по частям и замена переменной.
- •Определенные интегралы (интеграл Римана).
- •31.Понятие о несобственныхинтегралах I-города. Интегралывида (a , p 0 ).
- •32.Понятие о несобственныхинтегралах II-города. Интегралывида
- •Несобственные интегралы второго рода
- •Полярная система координат и криволинейный сектор.
- •35.Вычисление объемовтелпоплощадямпоперечныхсечений и объемовтел
- •36.Функции двухпеременных. Передел и непрерывность.Частныепроизводные, их
- •40.Формула Тейлорадляфункциидвухпеременных.
- •41.Экстремумы функциидвухпеременных. Необходимоеусловиесуществования
- •42.Экстремумы функциидвухпеременных. Достаточноеусловиесуществования
- •44.Определение двойногоинтеграла.
- •Что значит вычислить двойной интеграл?
- •50.Вычисление тройногоинтеграла в цилиндрической системекоординат.
- •52.Приложения тройногоинтеграла.
30.Определенный интеграл Римана. Методы вычисления: интегрирование по частям и замена переменной.
Определенные интегралы (интеграл Римана).
Пусть действительная функция f(x) определена и ограничена на ограниченном замкнутом интервале [a, b]. Разобъем этот интервал на n частичных интервалов точками
a = x0 < x1 < x2 < ... < xn = b.
Выберем
в каждом из частичных интервалов по
произвольной точке 

 и
составим сумму (интегральная сумма)
и
составим сумму (интегральная сумма) 

 .
.
Если
существует предел интегральной суммы
при стремлении к нулю длины наибольшего
частичного интервала разбиения: 
 ,
то функция f(x) называется интегрируемой
в смысле Римана на интервале [a, b].
Предел этой суммы
,
то функция f(x) называется интегрируемой
в смысле Римана на интервале [a, b].
Предел этой суммы







называется определенным
интегралом от f(x) по
интервалу [a, b] в
смысле Римана (интеграл Римана).
Это определение означает, что для любого
положительного числа  существует
такое число
существует
такое число  ,
что при любом разбиении интервала [a, b]
на частичные интервалы, длины которых
меньше
,
что при любом разбиении интервала [a, b]
на частичные интервалы, длины которых
меньше  .
.



и
при любом выборе промежуточных
точек  выполняется
неравенство
выполняется
неравенство





Функция f(x) называется подынтегральной функцией, а a и b - пределами интегрирования.
Интегрирование заменой переменной (метод подстановки) — один из самых часто встречающихся методов нахождения интегралов.
Цель введения новой переменной — упростить интегрирование. Лучший вариант — заменив переменную, получить относительно новой переменной табличный интеграл. Как определить, какую замену нужно сделать? Навыки приходят с опытом. Чем больше примеров решено, тем быстрее решаются следующие. На начальном этапе используем следующие рассуждения:

То есть. если под знаком интеграла мы видим произведение некоторой функции f(x) и ее производной f ‘(x), то то эту функцию f(x) нужно взять в качестве новой переменной t, поскольку дифференциал dt=f ‘(x)dx уже есть.
Рассмотрим, как работает метод замены переменной, на конкретных примерах.
Вычислить интегралы методом замены переменой:

Здесь 1/(1+x²) — производная от функции arctg x. Поэтому в качестве новой переменной t возьмемarctg x. Далее — воспользуемся таблицей интегралов:

После того, как нашли интеграл от t, выполняем обратную замену:


Если взять за t синус, то должна быть и его производная, косинус (с точностью до знака). Но косинуса в подынтегральном выражении нет. А вот если в качестве t взять экспоненту, все получается:





Чтобы получить нужный дифференциал dt, изменим знак в числителе и перед интегралом:

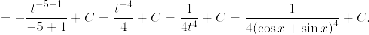

(Здесь
(ln(cosx))’ — производная
сложной функции. (Пусть
функция  определена
на множестве
определена
на множестве  и
и  –
множество значений этой функции. Пусть,
множество
–
множество значений этой функции. Пусть,
множество  является
областью определения функции
является
областью определения функции  .
Поставим в соответствие
каждому
.
Поставим в соответствие
каждому  из
из  число
число 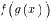 .
Тем самым на множестве
.
Тем самым на множестве  будет
задана функция
будет
задана функция  .
Ее называют композицией функций или
сложной функцией.
.
Ее называют композицией функций или
сложной функцией.
)
 )
)
31.Понятие о несобственныхинтегралах I-города. Интегралывида (a , p 0 ).
Рассмотрим обобщения понятия интеграла – интегралы с бесконечными пределами и интегралы от неограниченных функций. Это, по существу, новые понятия, поскольку при определении интеграла предполагалось, что отрезок интегрирования конечен, а подынтегральная функция определена и ограничена на этом отрезке. В новой же конструкции придется рассматривать пределы не только интегральных сумм, но и пределы определенных интегралов.
Пусть
функция  определена
для всех
определена
для всех  ,
где
,
где  -
некоторое число, и интегрируема на любом
отрезке
-
некоторое число, и интегрируема на любом
отрезке  ,
где
,
где  .
Если существует конечный предел
.
Если существует конечный предел
 ,
,
то
говорят, что функция  интегрируема в несобственном смысле
на промежутке
интегрируема в несобственном смысле
на промежутке  .
Этот предел называется несобственным
интегралом с бесконечным пределом или
несобственным интегралом первого рода
и обозначается
.
Этот предел называется несобственным
интегралом с бесконечным пределом или
несобственным интегралом первого рода
и обозначается

Обычно, если конечный предел существует, то говорят, что несобственный интеграл сходится. Если же конечного предела не существует, то говорят, что несобственный интеграл расходится.
Если с>a, то несобственные интегралы
 и
и  сходиться
или расходиться одновременно.
сходиться
или расходиться одновременно.
Действительно,
если для любого b>a функция  интегрируема,
то
интегрируема,
то
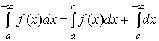 ,
откуда и следует что оба несобственных
интеграла одновременно или существуют,
или не существуют.
,
откуда и следует что оба несобственных
интеграла одновременно или существуют,
или не существуют.
Аналогично можно определить несобственные интегралы и для других бесконечных промежутков.
Если
функция  определена
при
определена
при  и
интегрируема на любом отрезке
и
интегрируема на любом отрезке  ,
где
,
где  ,
,
то
Если
же для функции  существуют
несобственные интегралы
существуют
несобственные интегралы  и
и  ,
то существует и несобственный интеграл
,
то существует и несобственный интеграл 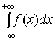 ,
определенный формулой
,
определенный формулой
 ,
,
причем
существование и значение несобственного
интеграла  не
зависят от выбора точки
не
зависят от выбора точки  .
.
Чтобы
лучше осознать идею, лежащую в основе
понятия несобственного интеграла,
рассмотрим положительную убывающую на
промежутке  функцию
функцию 
Интеграл 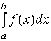 численно
равен площади фигуры, изображенной на
рисунке 10.1. При возрастании
численно
равен площади фигуры, изображенной на
рисунке 10.1. При возрастании  эта
площадь увеличивается и, если
эта
площадь увеличивается и, если  ,
то площадь может или возрастать
безгранично, или оставаться ограниченной,
то есть стремиться к некоторому пределу,
который представляет собой площадь,
заключенную между осью ОХ и кривой
,
то площадь может или возрастать
безгранично, или оставаться ограниченной,
то есть стремиться к некоторому пределу,
который представляет собой площадь,
заключенную между осью ОХ и кривой  вправо
от точки
вправо
от точки  .
.
Пример. Вычислить несобственный интеграл

Решение. По определению

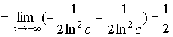
Несобственный интеграл сходится.
