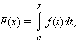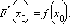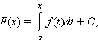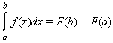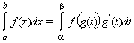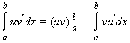29.Определенный интеграл с переменнымверхнимпределом. ФормулаНьютона- Лейбница.

Пусть на отрезке [a, b] задана интегрируемая функция 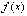. Известно, что определенный интеграл 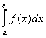 с геометрической точки зрения численно равен площади криволинейной трапеции.

Будем считать, что нижний предел 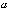 закреплен, а верхний предел меняется. Тогда будет меняться и значение интеграла, то есть он будет функцией верхнего предела интегрирования. Зададим любе значение 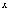 из отрезка [a, b] и введем в рассмотрение интеграл с переменным верхним пределом:

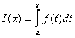  (1)

(От обозначения переменной интегрирования под знаком интеграла величина интеграла не зависит).

 

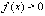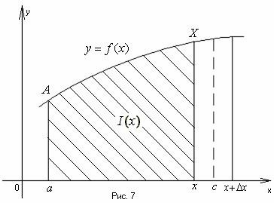
Если , то величина 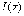 численно равна площади криволинейной трапеции 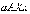 (рис. 7).

Очевидно, что эта площадь меняется в зависимости от изменения .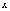

Рассмотрим свойства интеграла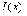 

1. Функция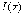 непрерывна на [a, b].

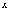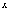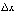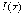Для доказательства фиксируем любую точку  отрезка и зададим приращение . При этом функция  получит приращение

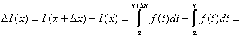(свойство 5)=

 

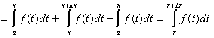
Устремим 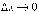, тогда 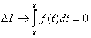 (свойство 2). Это и означает непрерывность функции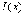 

2. Функция 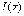 дифференцируема на отрезке [a, b].

Доказательство.

Применим теорему о среднем (свойство 9. ) к интегралу 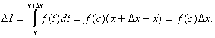 Получаем, что 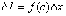, где 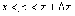 Делим обе части последнего равенства на 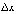и переходим к пределу при :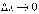

 

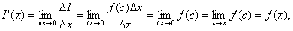
так как при 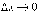переменная  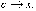Следовательно, в точке 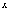 существует производная 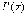, причем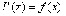 

Таким образом, доказано важное свойство:

Производная определенного интеграла от непрерывной функции 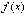по его верхнему пределу равна подынтегральной функции, вычисленной при верхнем пределе:

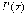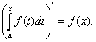  =  (2)

Замечание. Из доказанного свойства следует, в частности, что всякая непрерывная функция имеет первообразную. Согласно п. 5. 2. для непрерывной на [a, b] функции 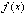 существует определенный интеграл 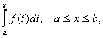то есть существует функция 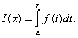 Так как 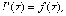 то 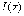 является первообразной для 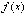 на отрезке [a, b].

ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ.

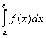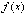Пусть требуется вычислить , где функция непрерывна на отрезке [a. b]. Введем новую переменную 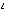 по формуле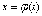. Не приводя доказательства, запишем формулу замены переменных

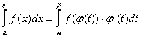. (3)

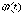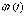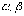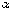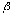При этом функции  и  должны быть непрерывны на отрезке [], концы которого  и  находятся из условий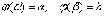 

Замечание.

Отметим, что при вычислении определенного интеграла по формуле (19) не нужно возвращаться к первоначальной переменной 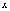, но необходимо пересчитать пределы интегрирования. В некоторых случаях быват удобнее вернуться к переменной 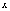 и ее пределам интегрирования.

Пример 3. Вычислить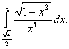 

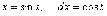
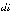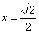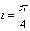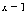Сделаем замену переменной  и определим новые пределы интегрирования  при ,  при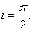 

Следовательно

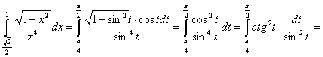
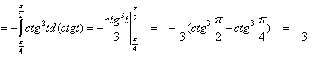
Если функция f (x) интегрируема на [a; b], то для любого 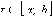 существует интеграл 

который называется интегралом с переменным верхним пределом.

Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.

Если функция f интегрируема на [a; b] и непрерывна в 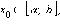 то функция F (x) дифференцируема в 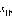 причем 

Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида 

где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.

 

Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:

Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда 

Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).

Пусть f (x) непрерывна на [a; b], g (t) имеет непрерывную производную на [α; β], 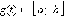 Тогда если a = g (α), b = g (β), то справедлива формула замены переменной в определенном интеграле: 

Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям: