
- •26.Интегральная сумма Римана. Определенный интеграл Римана. Интегрируемые
- •Геометрический смысл определенного интеграла
- •27.Определенный интегралРимана. Свойстваопределенногоинтеграла.Теорема о среднем.
- •28.Определенный интеграл с переменнымверхнимпределом. Теорема о егопроизводной.Существованиепервообразной непрерывной функции.
- •Доказательство.
- •Разбиение промежутка интегрирования
- •29.Определенный интеграл с переменнымверхнимпределом. ФормулаНьютона- Лейбница.
- •Доказательство.
- •30.Определенный интеграл Римана. Методы вычисления: интегрирование по частям и замена переменной.
- •Определенные интегралы (интеграл Римана).
- •31.Понятие о несобственныхинтегралах I-города. Интегралывида (a , p 0 ).
- •32.Понятие о несобственныхинтегралах II-города. Интегралывида
- •Несобственные интегралы второго рода
- •Полярная система координат и криволинейный сектор.
- •35.Вычисление объемовтелпоплощадямпоперечныхсечений и объемовтел
- •36.Функции двухпеременных. Передел и непрерывность.Частныепроизводные, их
- •40.Формула Тейлорадляфункциидвухпеременных.
- •41.Экстремумы функциидвухпеременных. Необходимоеусловиесуществования
- •42.Экстремумы функциидвухпеременных. Достаточноеусловиесуществования
- •44.Определение двойногоинтеграла.
- •Что значит вычислить двойной интеграл?
- •50.Вычисление тройногоинтеграла в цилиндрической системекоординат.
- •52.Приложения тройногоинтеграла.
Доказательство.
Применим
теорему о среднем (свойство 9. ) к
интегралу  Получаем,
что
Получаем,
что  ,
где
,
где  Делим
обе части последнего равенства на
Делим
обе части последнего равенства на  и
переходим к пределу при
и
переходим к пределу при  :
:

так
как при  переменная
переменная  Следовательно,
в точке
Следовательно,
в точке  существует
производная
существует
производная  ,
причем
,
причем 
Таким образом, доказано важное свойство:
Производная
определенного интеграла от непрерывной
функции  по
его верхнему пределу равна подынтегральной
функции, вычисленной при верхнем пределе:
по
его верхнему пределу равна подынтегральной
функции, вычисленной при верхнем пределе:
 =
=  (2)
(2)
Замечание. Из
доказанного свойства следует, в частности,
что всякая непрерывная функция имеет
первообразную. Согласно п. 5. 2. для
непрерывной на [a, b]
функции  существует
определенный интеграл
существует
определенный интеграл 
 то
есть существует функция
то
есть существует функция  Так
как
Так
как  то
то  является
первообразной для
является
первообразной для  на
отрезке [a, b].
на
отрезке [a, b].
Если
в определенном интеграле  изменять
верхний предел b, то будет меняться
и значение интеграла, то есть интеграл
будет функцией верхнего предела.
изменять
верхний предел b, то будет меняться
и значение интеграла, то есть интеграл
будет функцией верхнего предела.
Обозначим
верхний предел x, а переменную
интегрирования, чтобы не смешивать ее
с верхним пределом, обозначим t.
Таким образом, интеграл с переменным
верхним пределом является функцией
от x:  .
.
Имеет
место теорема: производная интеграла
с переменным верхним пределом от
непрерывной функции равна подынтегральной
функции, в которой переменная интегрирования
заменена верхним пределом: 
Доказательство. По определению производной
 где
где 
 [первый
интеграл представим в виде суммы двух
интегралов, пользуясь свойством
аддитивности]=
[первый
интеграл представим в виде суммы двух
интегралов, пользуясь свойством
аддитивности]=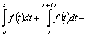
 [по
теореме о среднем]=
[по
теореме о среднем]= где
где 
Тогда следует
из определения непрерывной функции,
т.к. при
следует
из определения непрерывной функции,
т.к. при 
 .
Таким образом,
.
Таким образом, 
Это
значит, что интеграл с переменным верхним
пределом  является
первообразной для функции
является
первообразной для функции  .
.
Вычисление определенных интегралов путем нахождения числа, разделяющего множества сумм Дарбу, весьма громоздко. Гораздо проще вычислять определенный интеграл как разность значений первообразной. Но для этого нужно выяснить, какие из интегрируемых функций имеют первообразные. Мы докажем, что их имеют все непрерывные функции.
Разбиение промежутка интегрирования
Теорема
1. Если функция  интегрируема
на отрезках
интегрируема
на отрезках  и
и 
 ,
то она интегрируема и на отрезке
,
то она интегрируема и на отрезке 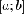 ,
причем выполняется равенство
,
причем выполняется равенство

|
(1) |
Доказательство. Возьмем
любое разбиение  отрезка
отрезка 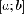 .
Не ограничивая общности рассуждений,
можно считать, что точка с является
одной из точек разбиения (в противном
случае мы присоединим ее к ним). Но тогда,
если, например,
.
Не ограничивая общности рассуждений,
можно считать, что точка с является
одной из точек разбиения (в противном
случае мы присоединим ее к ним). Но тогда,
если, например,  ,
каждая сумма Дарбу для отрезка
,
каждая сумма Дарбу для отрезка  распадается
на две суммы, соответствующие отрезкам
распадается
на две суммы, соответствующие отрезкам  и
и 
 и
и  где
где
Так
как функция  интегрируема
на отрезках
интегрируема
на отрезках  и
и  ,
то для любого
,
то для любого  найдутся
такие разбиения
найдутся
такие разбиения 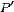 и
и  этих
отрезков, что
этих
отрезков, что

Эти
разбиения в совокупности образуют
разбиение  отрезка
отрезка  .
При этом имеем:
.
При этом имеем:

откуда
следует, что функция  интегрируема
и на отрезке
интегрируема
и на отрезке  .
.
Из
неравенств  и
и  следует,
что
следует,
что

Таким
образом, как 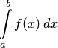 ,
так и
,
так и  разделяют
множества
разделяют
множества  и
и  сумм
Дарбу для отрезка
сумм
Дарбу для отрезка  .
Поскольку эти множества разделяются
лишь одним числом, то равенство (1)
доказано.
.
Поскольку эти множества разделяются
лишь одним числом, то равенство (1)
доказано.
Производная:
Рассмотрим функцию y = f(x), интегрируемую на отрезке [а, b]. Если х на промежутке [a, b], то функция f(x) интегрируема также на любом отрезке [а, х]. Предположим, что х меняется на отрезке [а, b], тогда на этом отрезке определена функция

(Переменную интегрирования обозначили буквой t, переменный верхний предел - буквой х).
Теорема 1. Если функция у = f(x) интегрируема на отрезке [а, b], то функция Ф(х) непрерывна на этом отрезке.
Теорема 2. Если подынтегральная функция непрерывна, то производная определенного интеграла с переменным верхним пределом существует и равна значению подынтегральной функции для этого предела. т.е.

Следствие 1. Если функция f(x) непрерывна на отрезке [а, b], то при любом х

Теорема
. : Если функция f непрерывна
на отрезке [a,b] , то она имеет
первообразную на этом отрезке, причем
первообразной для функции f является
интеграл с переменным верхним пределом
: и
поэтому
и
поэтому
 f(t)dt+C(8),
где С — произвольная константа.
f(t)dt+C(8),
где С — произвольная константа.
○Пусть x – произвольная точка отрезка [a,b]. По теореме о дифференцируемости интеграла функция F(x)определяемая формулой (1) ,имеет в точке x производную равную f(x) ,т.е.
F'(x)=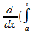 f(t)dt)=f(x) (9)
f(t)dt)=f(x) (9)
Согласно определению первообразной функция F(x) является первообразной для функции f(x) на отрезке [a,b]и поэтому справедливо равенство (8)●
Следствие : Из теоремы выше и теоремы из определения первообразной следует ,что всякая первообразнаяФ(x) для функции f ,непрерывной на отрезке [a,b] , имеет вид
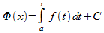 ,
,  (10),где
С – постоянная.
(10),где
С – постоянная.
