
- •26.Интегральная сумма Римана. Определенный интеграл Римана. Интегрируемые
- •Геометрический смысл определенного интеграла
- •27.Определенный интегралРимана. Свойстваопределенногоинтеграла.Теорема о среднем.
- •28.Определенный интеграл с переменнымверхнимпределом. Теорема о егопроизводной.Существованиепервообразной непрерывной функции.
- •Доказательство.
- •Разбиение промежутка интегрирования
- •29.Определенный интеграл с переменнымверхнимпределом. ФормулаНьютона- Лейбница.
- •Доказательство.
- •30.Определенный интеграл Римана. Методы вычисления: интегрирование по частям и замена переменной.
- •Определенные интегралы (интеграл Римана).
- •31.Понятие о несобственныхинтегралах I-города. Интегралывида (a , p 0 ).
- •32.Понятие о несобственныхинтегралах II-города. Интегралывида
- •Несобственные интегралы второго рода
- •Полярная система координат и криволинейный сектор.
- •35.Вычисление объемовтелпоплощадямпоперечныхсечений и объемовтел
- •36.Функции двухпеременных. Передел и непрерывность.Частныепроизводные, их
- •40.Формула Тейлорадляфункциидвухпеременных.
- •41.Экстремумы функциидвухпеременных. Необходимоеусловиесуществования
- •42.Экстремумы функциидвухпеременных. Достаточноеусловиесуществования
- •44.Определение двойногоинтеграла.
- •Что значит вычислить двойной интеграл?
- •50.Вычисление тройногоинтеграла в цилиндрической системекоординат.
- •52.Приложения тройногоинтеграла.
26.Интегральная сумма Римана. Определенный интеграл Римана. Интегрируемые
функции. Геометрическая интерпретация определенного интеграла.
Множество T = { xi } точек отрезка [ a, b ], таких, что a = x0 < x1 < x2 < …… <xT–1 <xT= b называетсяразбиением отрезка [ a, b ].
Обозначим Dxk длину отрезка [ xk-1 , xk ]. Тогда максимальное значение Dxk называется мелкостью разбиения T.
Если множество Т* включает в себя множество Т, то говорят, что разбиение Т* следует за разбиением Т; или что разбиение Т* вписано в разбиение Т.
Для двух разбиений Т и Т* всегда найдется разбиение, вписанное и в Т, и в Т*.
ОПРЕДЕЛЕНИЕ. Если функция f(x) задана всюду на отрезке [ a, b ] и задано разбиение Т, то всякая сумма:

называется интегральной суммой Римана функции f.
ОПРЕДЕЛЕНИЕ. Функция f(x) называется интегрируемой по Риману на отрезке [ a, b ], если для любой последовательности разбиений Тn отрезка [ a, b ], мелкость которых стремится к нулю; и для любого набора точек xkпоследовательность интегральных сумм sТn имеет один и тот же предел.
Предел
последовательности интегральных сумм
называют (определенным) интегралом
Римана функции f на
отрезке [a, b ] и обозначается  .
.
В
интеграле  число a называется нижним
пределом интегрирования, а b – верхним.
число a называется нижним
пределом интегрирования, а b – верхним.
Т. (необходимое условие интегрируемости.) Если функция интегрируема на некотором отрезке, то она ограничена на нем.
Из определения интеграла вытекает, что для любой последовательности разбиений с некоторого момента интегральные суммы будут отличаться от значения интеграла не более, чем скажем на 1. Т.е.

Предположим,
что существует неограниченная функция,
которая тем не менее является интегрируемой.
Возьмем произвольное разбиение отрезка Т.
Из неограниченности функции на отрезке
[ a, b ] вытекает, что по
крайней мере на одном из отрезков
[ xk-1 , xk ]
функция принимает сколь угодно большое
значение. Так как длина отрезка [ xk-1 ,
xk] фиксирована, то
всегда можно подобрать такую
последовательность точек, что 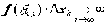 .
Если зафиксировать точки x на
прочих отрезках, тогда интегральная
сумма, рассчитанная без учета отрезка
[ xk-1 , xk ]
является фиксированной величиной, а
значит предел :
.
Если зафиксировать точки x на
прочих отрезках, тогда интегральная
сумма, рассчитанная без учета отрезка
[ xk-1 , xk ]
является фиксированной величиной, а
значит предел :

Следовательно, для любого разбиения множество возможных значений интегральных сумм не ограничено. А это противоречит следствию из определения интеграла, записанному выше.
Геометрический смысл определенного интеграла
Понятие определенного интеграла введено таким образом, что в случае, когда функция y = f(x) неотрицательна на отрезке [a; b], где a < b,

численно равен площади S под кривой y = f(x) на [a; b] (рис. 3).

Рис. 3
Действительно,
при стремлении  к
нулю ломаная (рис. 4) неограниченно
приближается к исходной кривой и площадь
под ломаной переходит в площадь под
кривой.
к
нулю ломаная (рис. 4) неограниченно
приближается к исходной кривой и площадь
под ломаной переходит в площадь под
кривой.

Рис. 4
Учитывая сказанное, можно указать значения некоторых интегралов, используя известные планиметрические формулы для площадей плоских фигур. Например,

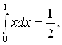
 и
т.д.
и
т.д.
(Первый из интегралов – площадь квадрата со стороной единичной длины; второй – площадь прямоугольного треугольника, оба катета которого единичной длины; третий – площадь четверти круга единичного радиуса).
