Структурная классификация систем

Следующий после этапа целевыявления этап разработки структуры системы начинается с выбора обобщенной структурной схемы проектируемой или совершенствуемой системы. В процессе структурного анализа классы систем разделяются по характеру отношений, независимо от состава элементов системы и их индивидуальных свойств. При этом для решения вопроса о принадлежности системы к тому или иному структурному классу достаточно рассмотреть ее обобщенную математическую модель.

Как было сказано ранее математическую модель системы, описываемой соотношением (2.1), определим как отношение непустых (абстрактных) множеств, представленных в виде соотношения

(m)^S = Def[(m)Q&ℜ (m) → (P∩Q = ∅)] , (2.1)

и рассмотрим весьма важный класс систем, обобщенная математическая модель которых определяется соотношениями (2.6) - (2.9):

S ⊂ _*{V_i : i ∈ I}, (2.6)

S ⊂ X _* Y. (2.7)

S : X → Y, (2.8)

(x, y) ∈ S ⇔ (∃C)[R(c, x) = y]. (2.9)

Систему, обобщенная математическая модель которой определяется соотношением (2.7), можно назвать активной, исходя из того, что понятия вход и выход объективно могут быть определены лишь для систем, взаимодействующих со средой.(Тогда C называется множеством глобальных состояний системы, а его элементы - просто глобальными состояниями системы, функция R называется глобальным откликом системы S).

При этом следует подчеркнуть существенную разницу между понятиями вход и входной объект, а также между понятиями выход и выходной объект.

Вход - это множество точек соприкосновения (терминальных точек) системы со средой, через которые среда может воздействовать на систему. Входной объект - это множество взаимодействующих факторов (химических, биологических, физических, информационных), приложенных к входным терминальным точкам.

Выход - это множество терминальных точек, через которые система может воздействовать на окружающую среду.

Выходной объект - множество факторов, регистрируемых на этих терминальных точках.

Поскольку вход и выход системы различимы только в процессе взаимодействия со средой, то системы, модели которых определяются соотношением (2.7), можно называть взаимодействующими.

Системы, у которых множество терминальных точек поддается разбиению на два качественно различающихся подмножества "вход" и "выход", удобнее называть битерминальными.

Поскольку организационные системы принадлежат к классу битерминальных систем и, в дальнейшем, будут рассматриваться только битерминальные системы, то для краткости термин "битерминальная" будет опускаться, хотя постоянно будут рассматриваться системы, имеющие вход и выход и удовлетворяющие соотношению (2.7).

Система может обладать определенными структурными свойствами в зависимости от характера отношений между входным и выходным объектами.

По характеру этих отношений, определяемому структурой системы, последняя может быть отнесена к одному из следующих классов систем:

функциональные, открытые, временные.

Кроме этого, система может иметь или не иметь обратную связь. При этом система может относиться или к одному из классов, или к нескольким из них, или ко всем классам одновременно, то есть быть, например, функциональной, открытой, временной и с обратной связью.

Подмножества систем, относящихся к перечисленным классам, являются независимыми и пересекающимися. Поэтому показать взаимосвязь между названными классами в виде декомпозиционного дерева не представляется возможным. Достаточно наглядно эта взаимосвязь демонстрируется с помощью связного графа, представленного на рис 3.1.

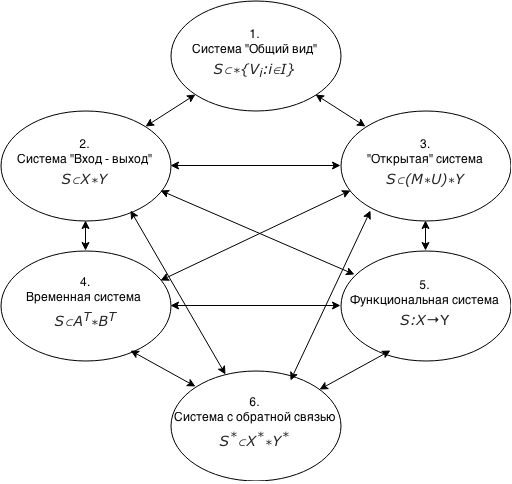
Рис. 2.3 Граф взаимосвязей между структурными классами систем

Система «Общий вид» S ⊂ _*{V_i : i ∈ I}, (2.6)

Система «Вход - выход» S ⊂ X _* Y. (2.7)

Открытая система S ⊂ (M _* U)_*Y. (2.17)

Функциональная система S : X → Y, (2.8)

Временная система S ⊂ A^T _* B^T (2.19)

Система с обратной связью S^*⊂ X ^*_* Y^* (2.21)

Из множества битерминальных систем выделяется подмножество таких систем, для которых S является функцией, то есть определяется соотношением (2.8). Все системы, модель которых определяется соотношением (2.8), являются функциональными. Функциональная система отличается тем, что между входным и выходным объектами имеется функциональная связь, значение которой позволяет полностью определить выходной объект системы при заданном входном объекте и известном начальном состоянии.

При этом имеется однозначная связь между всеми компонентами выходного и входного объектов.

Примером чисто функциональной системы является система алгебраических уравнений, для которой все значения решений (выходной объект) полностью определяются заданными значениями коэффициентов уравнений. К функциональным системам относится также, например, рентгеновская установка, на выходе которой рентгеновский снимок воспроизводит рентгеновское (функциональное!) изображение входного объекта.

Более жестким, чем определение функциональной системы, является определение функционально управляемой системы.

Система S ⊂ X_*Y является функционально управляемой тогда, и только тогда, когда

(∀y ∈ Y)(∃x ∈ X)((x, y) ∈ S), (2.12)

То есть, для любого значения y ∈ Y существует такое значение x ∈ X, что между x и y сохраняется функциональная связь, определяемая системой S.

Иными словами, любое наперед заданное значение y ∈ Y может быть получено путем подбора соответствующего значения x ∈ X.

Из приведенных примеров к функционально управляемым системам относится система алгебраических уравнений, которая может описывать либо абстрактную, либо конкретную систему.

Например, система абстрактных уравнений

L_o = L_i/K₁K₂, (2.13)

P_o = P_iK₁K₂, (2.14)

K₁ = S_o/S₁, (2.15)

K₂ = L₂/L₁, (2.16)

может быть соотнесена с конкретной функционально управляемой системой - гидравлическим домкратом. Для этого надо принять следующие определения:

L_o - длина перемещения выходного (силового) штока;

L_i - длина перемещения входного (управляющего) штока;

P_o - подъемная сила домкрата;

P_i - усилие противодействия на конце управляющего рычага;

S_o - площадь опорного (внутри гидравлической системы) сечения выходного штока; S₁ - площадь опорного сечения входного штока;

L₁ - длина опорной части управляющего рычага;

L₂ - длина управляющего рычага от точки соединения с входным штоком до конца.

Если все коэффициенты S_i, S_o, L₁, L₂ не имеют числовых значений, то система алгебраических уравнений (2.13) - (2.16) является математической моделью абстрактного гидравлического домкрата.

Если же этим коэффициентам заданы конкретные числовые значения, то она превращается в математическую модель конкретной системы, позволяющую вычислять усилие противодействия на управляющем рычаге P_i в зависимости от поднимаемого груза P_o и длину перемещения выходного штока (высоту подъема груза) L_o.

Для значительного числа систем, с которыми приходится сталкиваться на практике, непосредственная функциональная связь между входным и выходным объектами не может быть определена ни экспериментальным, ни аналитическим путем. Особенно это относится к организационным системам. Это связано с тем, что поведение системы определяется не только задаваемыми на вход воздействиями, но и совокупностью воздействий, поступающих из внешней среды и не поддающихся управлению. Такие системы будем называть открытыми.

Более строго сформулировать понятие открытой системы можно, разделив входной объект на две составляющие, то есть

X = M ∪ U.

Тогда система определяется как

S ⊂ (M _* U)_*Y. (2.17)

Пусть составляющая M представляет совокупность измеримых, непосредственно наблюдаемых воздействий, а U - те входные воздействия, о которых имеется только косвенная (если она вообще есть) информация.

Тогда для любого заданного m ∈ M о соответствующей выходной величине известно лишь то, что она должна принадлежать множеству

Y_m = S(m, U_m).

Такая система и является открытой в общем смысле.

Строго говоря, элементы “открытости” то есть непредсказуемости поведения присущи любой системе - это ошибки, сбои в работе, отказы. Вопрос лишь в том, каков удельный вес этой непредсказуемости по сравнению с функциональной управляемостью системы. Здесь уместно привести аналогию со случайными и детерминированными величинами и вспомнить, что любая измеряемая величина, относящаяся к конкретному объекту (длина, диаметр, вес и т. п.) является, строго говоря, величиной случайной. Однако если диапазон случайных отклонений величины от ее номинала не велик, то она считается детерминированной. Следовательно, открытая система при определенных условиях может быть сведена к функциональной и наоборот.

Если элементами входного и выходного объектов системы являются временные функции, то такая система будет являться временной системой. Для временных систем элементы входного и выходного объектов определены на одном и том же множестве моментов времени, то есть

X ⊂ A^T; Y ⊂ B^T. (2.18)

Таким образом, для временных систем

S ⊂ A^T _* B^T. (2.19)

Элементами множеств X и Y служат абстрактные функции времени

x : T → A; y : T → B.

Значения функций из X и Y в момент времени t обозначаются соответственно через x(t), y(t).

Если исследованию подвергаются физиологические процессы в живых организмах, в том числе и у человека, то в большинстве случаев адекватной моделью для таких процессов будут являться временные системы.