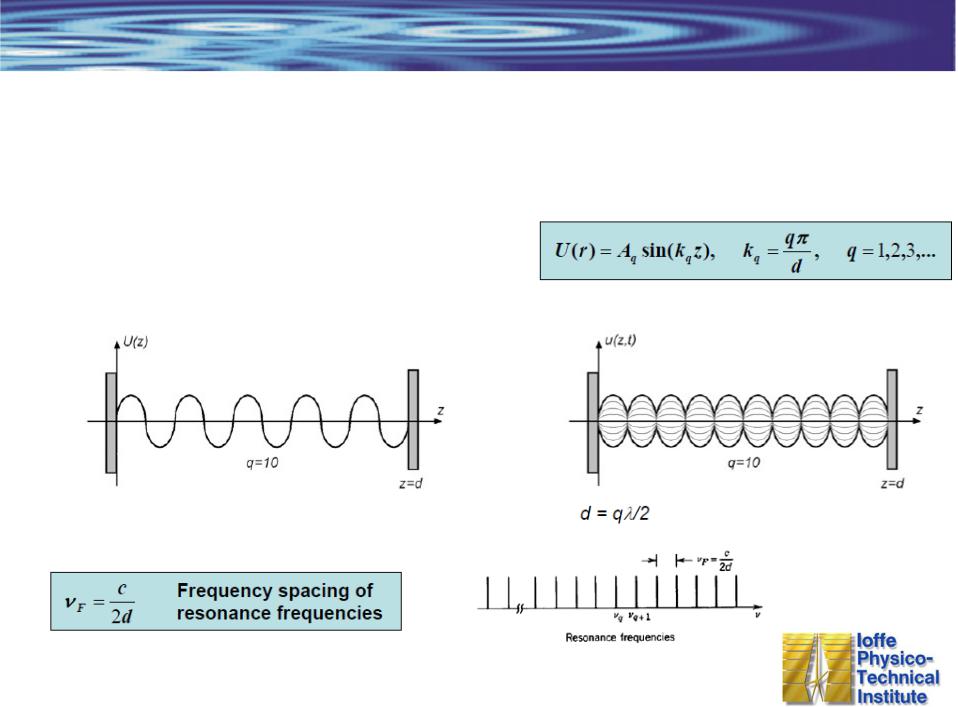
Эталон Фабри-Перо
Два плоских зеркала на расстоянии d (без потерь)
u(r,t) Re U r exp j2 t |
2U r k 2U r 0; |
|
U (z 0) U (z d ) 0 |
Решение в виде стоячих волн
дискретный набор частот (продольные моды)
Свободный спектральный диапазон (FSR)
Пример: d = 15 см, n = 1, FSR = 1 ГГц
Эталон Фабри-Перо
Продольная мода резонатора самовоспроизводится при прохождении круга
Эталон Фабри-Перо
Потери и спектральная ширина
Зеркала имеют конечное отражение
(R<1 –коэффициент отражения по интенсивности)
Сходящаяся геометрическая прогрессия
F – параметр характеризующий добротность резонатора
Эталон Фабри-Перо
Потери и F
Время жизни фотонов в резонаторе
Через приведенные потери к единице длины резонатора можно выразить экспоненциальное
затухание |
Соотношение неопределенности |
|
Добротность
Обычно очень высокий
Резонатор как спектроанализатор
Резонатор Фабри-Перо со сферическими зеркалами
Резонатор с плоскими зеркалами требует высокую точность юстировки
Сферические зеркала более устойчивы к рассогласованию
Для меридиальных лучей в приближении лучевой оптики
(пересекают оптическую ось)
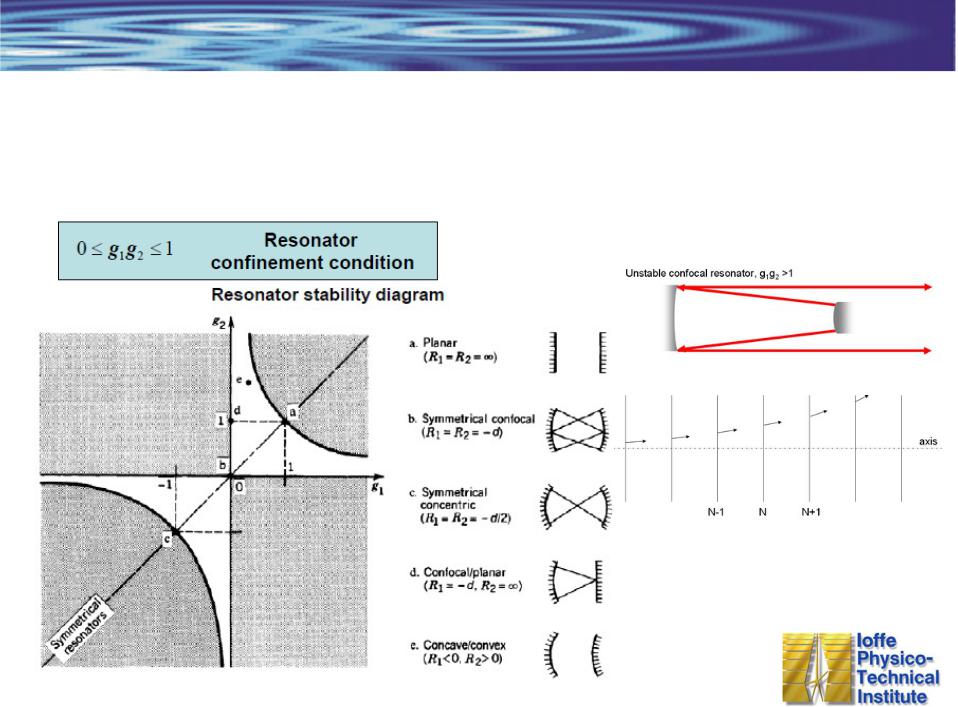
Продольные моды резонатора со сферическими зеркалами
Резонатор с плоскими зеркалами требует высокую точность юстировки
Симметричный резонатор стабилен только для вогнутых зеркал R<0
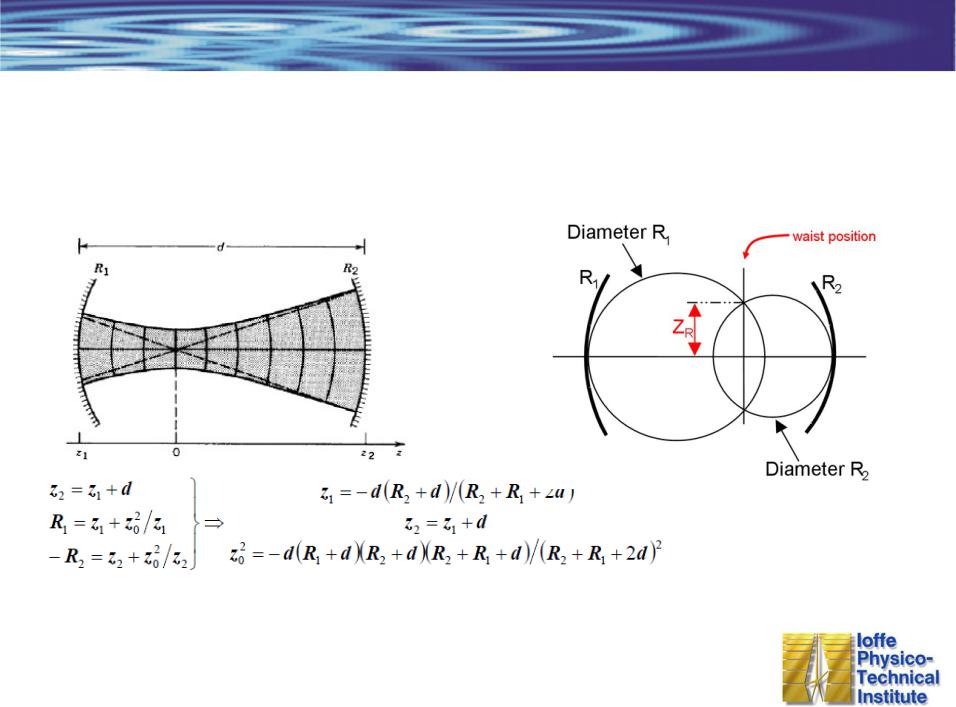
Гауссов пучок как фундаментальная поперечная мода резонатора со сферическими зеркалами
Радиус кривизны поверхности зеркал должен совпадать с радиусом кривизны волнового фронта
Резонатор с плоскими зеркалами требует высокую точность юстировки
Поперечные моды резонатора со сферическими зеркалами
Эрмитовы моды имеют тот же радиус кривизны волнового фронта, что и Гауссов пучок, поэтому тоже являются собственными модами резонатора.
Однако при прохождении резонатора различные моды будут приобретать различный набег фазы.
Разным индексам будут соответствовать разные резонансные частоты