
- •Лекция 13: Нелинейные оптические эффекты
- •Нелинейная оптика
- •Нелинейная оптика
- •Нелинейные оптические эффекты
- •Нелинейные оптические эффекты
- •Нелинейные оптические эффекты
- •Нелинейные оптические эффекты
- •Параметрические процессы
- •Генерация второй гармоники
- •Генерация второй гармоники
- •Фазовый синхронизм
- •Выполнение условий фазового синхронизма
- •Выполнение условий фазового синхронизма
- •Оптический параметрический резонатор (OPO)
- •Нелинейность третьего порядка
- •Рассеяние на фононах
- •Эффект Рамана (спонтанное рассеяние)
- •Вынужденное комбинационное рассеяние (ВКР, SRS)
- •Рассеяние Мандельштама - Бриллюэна
- •Рассеяние Мандельштама - Бриллюэна
- •John and canal defined of
- •Солитоны в океане: The “Rogue” Wave
- •Оптические солитоны
- •Optical Solitons
- •Пространственные солитоны
- •Временные солитоны
- •Пространственно – временной солитон «оптическая пуля»
- •Нелинейное волновое уравнение
- •Солитоны высших порядков
- •Когерентное взаимодействие: волна или частица
- •Рождение третьего солитона при столкновении

Лекция 13: Нелинейные оптические эффекты

Нелинейная оптика
•Линейная оптика – оптика «слабого» света, нет изменения (генерации) частоты.
•Нелинейная оптика – оптика света большой интенсивности. Возникновение новых частот.
Материалы
Title |
Transmission Range, mm |
Typical Applications |
|
LBO |
0.16 |
- 3.3 |
High power lasers harmonics generation and OPO pumped by |
|
|
|
Nd:YAG harmonics |
BBO |
0.19 |
- 3.3 |
- Solid State and Dye laser harmonics generation with output |
in |
|
|
the range 200-532 nm; |
|
|
|
- OPO/OPA pumped by Nd:YAG harmonics with 295 - 3000 |
|
|
|
nm output |
KTP |
0.38 |
- 4.4 |
Harmonics generation in UV and VIS |
KD*P |
0.26 |
- 1.6 |
Harmonics generation in VIS |
LiNbO3 |
0.4 - 4.5 |
SHG and OPO pumped by Nd:YAG laser |
|
LiIO3 |
0.3 - 6.0 |
SHG and THG of Nd:YAG, DFM with output in 3 - 5 m range |
|
AgGaS2 0.53 – 12 |
Harmonics generation and DFM with wide tunable output in 3 - |
||
|
|
|
9 m, IR visualization |
AgGaSe2 |
0.73 – 18 |
SHG of CO2 lasers, OPO with 3 - 12 m output |
|
GaSe |
0.65 – 18 |
SHG of CO and CO2 lasers, DFM with output in 7 - 16 m |
|
CdSe |
0.75 – 25 |
DFM with tunable output up to 25 m |
|
AgAsS3 |
0.6 – 13 |
IR visualization, DFM, OPO |
|
Te |
3.8 – 32 |
DFM with output in 15 - 30 m |
|
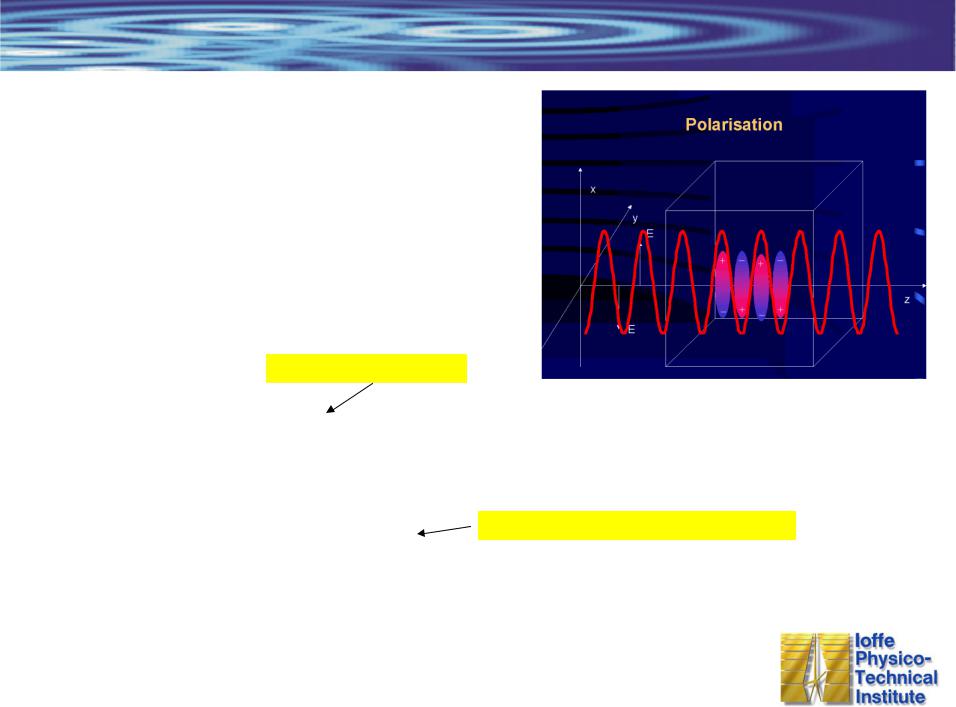
Нелинейная оптика
Большие интенсивности
D 0E P; P 0 1E 0 2 E2 3E3 PL PNL
2 |
2 |
|
1 2 E |
|
4 2 P |
|
|
|
||
E |
|
|
|
|
t2 |
|
c2 t2 |
|
|
|
|
c2 |
|
|
Источник новых электромагнитных волн |
||||||
2 |
2 |
|
2 |
|
|
|
4 2 P ( ) |
|||
E c2 1 4 1 E |
|
NL |
|
|||||||
c2 |
t2 |
|
||||||||
PNL ( ) |
|
|
|
|
|
|
||||
0 ijk(2) E j Ek ijkl(3) E j Ek El |
||||||||||
|
|
|
|
|
|
|
jk |
|
jkl |
|

Нелинейные оптические эффекты
PNL ( ) 0 ijk(2) E j Ek
jk
•Электрооптический эффект, оптическое выпрямление, генерация гармоник, параметрическое усиление и волновое смешение.
PNL ( ) 0 ijkl(3) E j Ek El
jkl
•Зависимый от интенсивности показатель преломления: эффект Керра, самофокусировка, само и кросс фазовая модуляция, оптические солитоны.
•Рассеяния (взаимодействие с другими волнами) спонтанные и вынужденные: Рамановское (ВКР), бриллюэновское (ВРМБ),

Нелинейные оптические эффекты
|
|
|
|
|
2 |
1 4 1 E |
|
4 2 P ( ) |
|
|
|
|
|
||||||||||
2 |
E |
2 |
|
|
|
|
(2) |
Ek |
|
||||||||||||||
|
|
|
|
2 |
|
2 |
|
|
2 |
PNL ( ) 0 ijk E j |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NL |
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
c |
|
|
|
t |
|
|
jk |
|
|
|
|
|
В анизотропной среде – тензорное описание |
|
|
|
|
|||||||||||||||||
|
P |
|
|
(t) 0 2 ( 3, 1 |
, 2 )E |
|
E |
2 Взаимодействие двух волн |
|
|
|
||||||||||||
|
|
|
3 |
|
|
|
|
ˆ |
|
|
|
|
1 |
|
|
|
|
||||||
|
3 1 2 |
|
Закон сохранения энергии |
|
|
|
|
|
|||||||||||||||
|
Pi 3 (t) 0 |
ijk(2) ( 3, 1, 2 )E j 1 Ek 2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
j,k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pi ( 3 ) 0 ijk(2) ( 3, 1, 2 )E j ( 1)Ek ( 2 ) exp j k3 k2 |
k1 r |
|
|
|||||||||||||||||||
|
ijk(2) |
2dijk Тензор определяется симметрией |
|
|
|
|
|
||||||||||||||||
|
ijk(2) |
0 |
|
При инверсной симметрии |
|
|
|
|
|
|
|||||||||||||
|
|
|
Симметрия Клеймана |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
(2) ( , , ) (2) |
( , , ) etc. |
11 1; |
22 2; |
33 3 |
|
|
||||||||||||||
|
|
|
|
ijk |
|
|
3 |
1 2 |
ikj |
|
3 |
|
1 |
2 |
|
3D тензор превращается в 2D |
|||||||
|
|
ijk(2) ( 3, 1, 2 ) * ijk(2) ( 3, 1, 2 ) |
23 4; |
31 5; |
12 6 |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
ijk(2) (jik2) (jki2) d14 d25 |
|
d36 |
|
|
|
|
|
|
||||||||||||
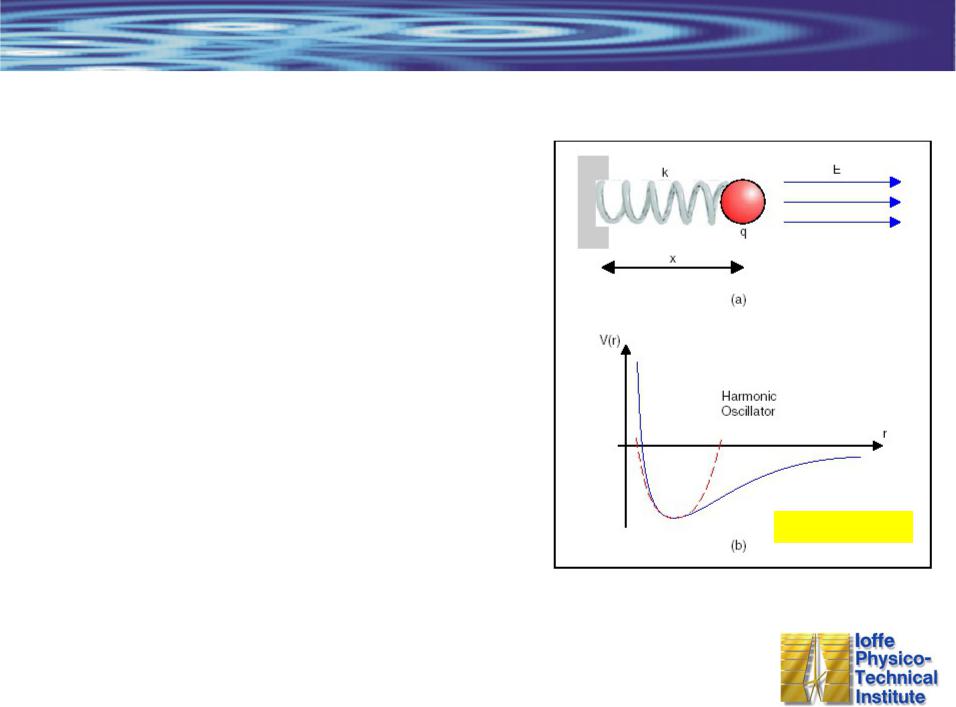
Нелинейные оптические эффекты
Микроскопическая природа
V (x) 1 kx2 |
|
1 bx3 |
1 cx4 ;b,c k |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2 |
|
|
|
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
b,c 0 гармоническй потенциал |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
F(x) |
V |
kx bx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F ( ) k b 2 ; F ( ) k b 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
d 22x 2 dx |
|
|
k |
x |
|
b |
x2 |
c |
|
x3 |
e |
E( ) exp j t E* ( ) exp |
j t |
|||||||||||||||||||||
|
|
|
|
m |
m |
|
||||||||||||||||||||||||||||
dt |
|
|
|
|
dt |
|
|
m |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|||||||||
x(t) |
|
x1 |
exp j t |
x2 |
|
exp j2 t |
Движение электрона |
|
||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x |
|
e |
|
E |
( ) |
|
|
|
|
|
|
1 |
|
|
|
( ) |
Ne2 |
E( ) |
|
1 |
|
|
||||||||||||
m |
2 |
2 2 j |
|
m |
|
2 |
2 |
2 j |
|
|||||||||||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
0 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
x2 |
|
be2 |
|
E2 ( ) |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
; |
|
|
|
|
|||||||||
|
2m3 |
|
02 |
4 2 4 j 02 2 |
2 j 2 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
P2 (t) 1 |
P(2 )exp |
j2 t c.c. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d (2 ) |
|
|
bNe3 |
|
|
|
E( ) |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
2m3 0 |
|
|
02 4 2 4 j 02 2 2 j 2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
bN 2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
d (2 ) |
|
|
|
|
|
0 |
1(2 ) 1( ) |
m / V |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2N |
2 3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Несимметричный потенциал
V ( x) V (x)
Нелинейные оптические эффекты
|
|
|
|
2 |
1 4 1 E |
4 2 P ( ) |
|
|
||||
2 |
E |
2 |
|
(2) |
E j ( 1) Ek ( 2 ) |
|||||||
|
|
|
2 |
|
2 |
|
2 |
PNL ( 3 ) 0 ijk |
||||
|
|
|
|
|
|
|
|
|
NL |
|
|
|
|
|
|
|
c |
|
|
c |
|
t |
|
jk |
|
Электрооптический эффект – частный случай нелинейно-оптического эффекта
Pi ( 1) 0 ijk(2) ( 1, 1,0)E j ( 1)Ek (0)
ijk(2) ( 1, 1,0) kij(2) (0, 1, 1)
Из симметрии существует эффект оптического выпрямления Световая волна порождает постоянное электрическое поле
Оптическое выпрямление |
|
Генерация второй гармоники |
||||
PNL |
|
2 1; |
k1 k2 |
|
2 1; |
k1 k2 |
|
3 1 1 0 |
PNL |
3 1 1 2 1 |
|||
|
||||||
|
|
k3 k1 k1 0 |
|
k3 k1 k1 2k1 |
||
Параметрические процессы
p s i |
|
|
Параметрическое усиление p i s |
||
kp ks ki |
p |
s |
|
|
|
s |
PNL |
i |
|
|
|
Up конверсия |
1 |
2 3 |
Дифференциальная частота |
1 |
2 3 |
|
Видимый (мощный) |
1 |
2 |
Видимый |
|
1 |
2 |
|
|
|
||||
|
|
Видимый |
|
|
|
|
PNL |
|
|
Видимый |
PNL |
Дальний ИК |
|
|
|
|
|
|
||
ИК (слабый)

Генерация второй гармоники
Кристаллы: KH2PO4 (KDP), lithium triborate (LBO) and β-barium borate (BBO), KNbO3, LiNbO3.
E(z,t) |
|
|
1 |
|
ˆ |
|
( 1) exp |
j k1z 1t c.c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
2 |
e E |
|
Падающая волна |
|||||||||||||||||||||||||||||||||||||||||||||||||
PNL Pi |
2 E2 ( 1) ijk ej ek exp j 2k1z |
2 1t Наведенная поляризация на удвоенной частоте |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Даже при поперечной падающей волне у второй гармоники есть поляризация вдоль z |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
PNL P |
|
|
|
NL |
PNL E2 ( 1 ) ijk ej ek exp j 2k1z |
2 1t |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E(z, 2 ) E |
|
|
|
(z, 2 ) E (z, 2 ) |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NL |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
4 2 |
|
NL |
|
|
|
|
|
|
|
|
|
|
4 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
E |
|
|
2 |
P |
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
2 P |
|
|
|
|
z |
||||||||||||||
|
|
|
|
2 c2 |
|
|
|
2 c2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
E |
|
|
|
|
4 P |
|
|
|
NL 0 |
В приближении заданного поля |
|
|
|||||||||||||||||||||||||||||||||||||
|
z |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Генерация второй гармоники
E |
|
|
|
|
|
) 4 P |
|
|
|
NL (z, |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
(z, |
|
|
|
); |
|
|
|
|
|
|
|
|
|
|
k |
2 |
|
|
|
(2 ); k 2k k |
2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
1 |
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
NL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
k2 |
E (z, 2 ) |
|
|
|
2 |
2 P |
(z, 2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
E (z, 2 ) медленно меняющаяся амплитуда |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
z2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) E2 |
|
|
|
|
|
|
|
|
|
|
kz |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 2 |
|
|
|
|
kz sin |
2 |
|
|
|
|||||||||||||||||||||||||||||
|
E |
|
( |
|
, z) j |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
exp |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
2k2 |
|
|
|
|
|
|
|
|
|
2 |
|
k |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
(2) |
|
2 |
|
|
|
|
|
|
|
|
sin |
2 |
kz |
|
|
|
Вектор Пойнтинга |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
S( 2 , z) |
8 2 |
|
|
|
|
|
|
E 1 |
|
4 |
|
|
|
|
2 |
|
|
|
|
|
Мощность второй гармоники |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
Условия фазового синхронизма (закон сохранения импульса) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
2 |
kz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
Линейный рост мощности |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
