4.6. Упрочняющее действие границ зерен

Границы зёрен упрочняют металл. Эффект упрочнения может быть объяснён несколькими эффектами. (Здесь не рассматривается взаимодействие дислокаций с границами, которое увеличивается с уменьшением зерен).

Модель Пётча-Холла.

По исследованиям влияния размеров зерен на предел текучести _т металлов накоплен достаточно богатый экспериментальный материал. Полученные опытным путем зависимости σ_т(d), где d − размер зерна (напомним, что зерно в общем случае - полиэдр), достаточно хорошо описывались математической зависимостью вида

, (4.12)

где ₀ учитывает упрочнение за счет других причин; K  коэффициент упрочнения за счет границ.

Это соотношение было предложено Пётчем и Холлом и носит их имена. Таким образом, зависимость (4.12) является аппроксимацией экспериментальных данных, которая хорошо работает при размерах зерна от 10 до 200 мкм. Отметим, что влияние границ зерен на прочность металла сводится обычно не к общей протяженности границ (или их плотности), а к размеру зерна, с которым протяженность границ связана квадратичной зависимостью.

Модель аккомодационных зон.

Дадим качественное объяснение влиянию границ (предыдущее объяснение количественное, без объяснения механизма упрочнения). Относительно направления действия внешних напряжений кристаллическая решётка соседних зерен в металле ориентирована различно. Преимущественное скольжение дислокаций в них происходит по различным системам скольжения (плоскостям и направлениям) относительно внешних напряжений. Внутри зёрен действуют 1 – 2 системы скольжения (Рис. 4.15а.). Для того чтобы обеспечить неразрывность деформации соседних зерен (без образования трещин), в приграничных областях должно работать не менее пяти систем скольжения (правило Мизеса-Тейлора). Вследствие этого вблизи границ плотность дислокаций, а следовательно, и упрочнение от их взаимодействия с границами и между собой, выше, чем в областях зерна, удаленных от границ.

Рис. 4.15а. Соотношение зон простого и аккомодационного скольжения (d-2t)/d в зёрнах большого и малого размера.

Толщина t этих, так называемых аккомодационных зон, где происходит «приспособление» деформации одного зерна к другому без образования трещин, есть величина приблизительно постоянная для любого размера зерна.

Таким образом, при увеличении радиуса зерна r изменение относительного объема упрочненных приграничных зон в зависимости от радиуса зерна r может быть приближенно описано соотношением

, (4.13)

г

Рис. 4.16. Схема к расчету упрочнения металла

за счёт напряжений от границ зерен

а, б – большое и маленькое зёрна.

деv_упр/v  относительный объем упрочненного за счет аккомодационных зон металла; r  средний радиус зерна; t  толщина упрочненной аккомодационной зоны. То есть с уменьшением диаметра зёрен увеличивается относительный объём более упрочнённых приграничных зон и, соответственно, средняя прочность.

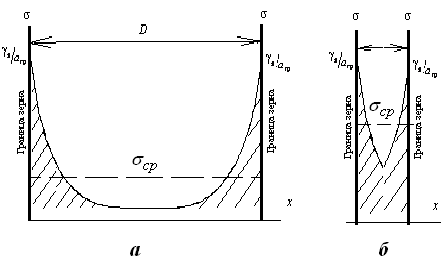
Модель напряжений от границ (рис.4.16).

В предыдущем разделе мы упоминали о том, что границы зерен создают свои поля напряжений. Выполним оценку величины напряжений, которую дают границы в среднем по объему металла. Примем для простоты, что «среднее» зерно в металле имеет форму куба. Это зерно окружено границами с энергией , которые создают в зерненапряжения σ_гр=/х, максимальное значение которых /,рис. 4.16. При удалении от границ эти напряжения уменьшаются и на расстоянии 10а не превышают 10% от максимальных.

Найдем усредненные по объему зерна напряжения, создаваемые плоскими дефектами  границами. Пусть объем зерна v~d³, площадь его поверхности, т. е. площадь границ, s=6d³. Тогда средние по объему зерна напряжения рассчитаем следующим образом:

. (4.14)

Будем считать, что напряжения от противоположных границ _гр= _s^'/x симметричны. Тогда операцию интегрирования можно выполнить для одной ветви _гр и полученное значение удвоить:

. (4.15)

Н

Рис. 4.17. Зависимость упрочнения от размера зерна

согласно зависимостям: 1  Петча-Холла y=1/x^0,5;

2  близкой к модели Петча-Холла y=1,2/x^0,7;

3  аккомодационных зон y=1[(x1)]³;

4  по (4.15) y=0,123(lnx8,11)/x

апример, для железа при_s^'= 1,2 Дж/м², диаметре зерна

D = 2010^6 м (20 мкм),

параметре решетки на границе = 310^10 м получим

_гр  8 МПа.

При увеличении размера зерна вдвое

(d = 40 мкм)

напряжения от действия границ снижаются до значений _гр = 4,2 МПа,

т.е. почти в 2 раза.

Таким образом, границы, казалось бы, не создают значительного упрочнения по металлу в среднем (4 – 8 МПа - это много меньше предела текучести железа). Для объяснения этого эффекта можно воспользоваться наглядной моделью: волейбольную сетку стянем пальцами руки с некоторой силой, т.е. зададим деформацию сетки и создадим при этом напряжения. Представим теперь, что жесткость материала сетки возрастает, например, она становится толще. Это аналогично повышению модуля упругости металла. Наши пальцы при этом ощущают все большие напряжения при увеличении жесткости материала сетки. Так возрастают и внутренние напряжения в металле. Таким образом, те границы, которые возникли при более высоких температурах, создают большие напряжения, чем границы с такой же энергией , но образованные при более низких температурах. Поэтому нельзя оценивать влияние размера зерна (или протяженности границ) на прочность металла, не зная их происхождения.

На рис. 4.17 представлен характер зависимостей предела текучести металла (в безразмерном виде) от размера зерна, рассчитанных по соотношениям (4.12), (4.13) и (4.15). Видно, что кривые на графике достаточно близки друг к другу.Эффект упрочнения достигается от всех рассмотренных механизмов совместно.