1.3. Методы исследования текстуры

Для определения текстуры применяются прямые и косвенные методы.

К прямым относятся рентгенографический, оптический и металлографический методы.

К косвенным - оценка текстуры по анизотропии физических или механических свойств/1.78, 1.115, 1.251, 1.252/.

Прямые методы

Металлографический метод основан на том, что различные кристаллографические плоскости взаимодействуют с различной интенсивностью с химическими реактивами. Например, за одно и то же время взаимодействия образуют в окислительной среде оксиды различной толщины, которые имеют различные цветовые оттенки (желтый, зеленый, красный и т.д.). Выполнив травление в заданных условиях, можно определить долю зерен, окрашенных, например, в красный цвет, который дает в использованном реактиве плоскость, например, (111). Доля красного цвета на поверхности исследованного шлифа покажет долю зерен, ориентированных гранью (111) в плоскости образца, вырезанного, например, из листа.

Другой способ – определение ориентировок зёрен по форме ямок травления

Рентгеновский метод основан на явлении дифракции рентгеновских лучей. По данным рентгенографического измерения строится полюсная фигура по плотности распределения полюсов в пространстве вокруг поликри­сталлического образца. Плотность распределения полюсов выводится из про­странственного распределения интенсивности дифрагировавших рентгеновских лучей, отраженных от определенной кристаллографической плоскости. Этот метод пригоден лишь для случая, когда размеры зерен в поликристалле настолько малы, что в изучаемой области образца содержится достаточно большое число кристаллитов.

При исследовании таких образцов используются методы регистрации рентгеновских лучей с помощью счетчика, позволяющие выполнять количе­ственный анализ деталей рассеяния ориентировок зерен. Метод основан на измерении интенсивности отраженных рентгеновских лучей от исследуемого образца, попадающих в щель счетчика импульсов.

Основным устройством для изучения текстуры с помощью счетчика служит гониометр, работающий по принципу Брэгга-Брентано.

Для получения полюсной фигуры необходимо ориентированные иначе плоскости семейства {hkl} привести в отражающее положение. Поскольку счетчик регистрирует только интенсивности на экваторе круга отражений, то при повороте образца вокруг направления, лежащего на его поверхности, в отражающее положение приводятся все кристаллографические плоскости, нормали которых наклонены к поверхности образца и выходят на диаметр образца, перпендикулярный оси поворота. Далее, вращением образца вокруг нормали к его поверхности будут охватываться все плоскости решетки, нор­мали которых образуют конус вокруг нормали образца.

Рентгенографический метод основан на явлении дифракции рентгеновских лучей. Поток рентгеновских лучей определенной длины волны испускает рентгеновская трубка (рис. 7.3). Он проходит сквозь узкую щель и попадает на исследуемый образец, который имеет форму диска и помещен на поворотный столик. Поворотный столик позволяет образцу вращаться вокруг собственной оси y на угол β, а также поворачиваться на угол α вокруг оси х, изменяя положение образца относительно падающего потока рентгеновского излучения.

Каждой кристаллографической плоскости (hkl), согласно закону Вульфа-Брегга, соответствует свой угол отражения для излучения определенной длины волны

, (7.1)

где λ  длина волны излучения; n  порядок отражения; d  межплоскостное расстояние исследуемой плоскости (hkl). Тогда при заданных λ, d имеем вполне определенный угол отражения θ для плоскости (hkl).

Рис. 7.3. Схема рентгеновской установки для исследования кристаллографической текстуры: 1рентгеновская трубка;2входная диафрагма;3счетчик отраженных импульсов;4поворотный столик с образцом

Индексы кристаллографических плоскостей, которые могут дать отражение, определяются установкой счетчика. Угол 2 между продолжением первичного луча и отраженнымлучом, попадающим в щель счетчика, связан с индексами отражающих плоскостей {hkl} следующей формулой:

где а - параметр кубической решетки;  - длина волны используемого ха­рактеристического излучения; п - порядок отражения.

Для описания текстуры поликристаллических материалов широко ис­пользуется метод построения прямых и обратных полюсных фигур.

Прямая полюсная фигура {HKL} представляет собой стереографическую проекцию выходов нормалей к одной заданной плоскости {hkl} для всех кристаллов поликристалла и обозначается индексами этой плоскости,

13

т.е. это - диаграмма распределения полюсной плотности образца. Для ее по­строения первоначально снимают текстурную кривую {HKL}.

Для съемки и построения полной прямой полюсной фигуры совмещают два метода съемки - на отражение (метод Шульца) и на просвет. Положение счетчика по отношению к рентгеновскому пучку при съемке одной текстурной кривой не изменяется. Положение образца зависит от метода съемки.

При съемке на отражение зарегистрированная счетчиком интенсивность рентгеновских лучей пропорциональна количеству кристаллов, ориен­тированных так, что нормаль к отражающей кристаллографической плоскости совпадает с (hkl)

Для получения текстурной кривой {HKL} выполняется поворот образца вокруг оси приставки. Кроме того, при съемке на отражение осуществляется поворот вокруг оси, а при съемке на просвет - вокруг вертикали, параллельной поверхности образца. Соотношение наклона образца и вращения вокруг оси приставки для каждого из металлов определяет шаг спирали для построения полюсной фигуры. Поворот исследуемого образца производится либо непрерывно, либо ступенчато по углам альфа с одновременной записью интенсивности зарегистрированного счетчиком пучка.

При исследовании листовых материалов обычно плоскостью проекции для прямых полюсных фигур является плоскость прокатки. За системы коор­динат принимают направления прокатки (НП), поперечное направление (ПН) и направление нормали (НН) к плоскости прокатки. На плоскости проекций НП и ПН изобразятся полюсами на пересечении вертикального и горизонтального диаметров соответственно с большим кругом проекций, а НН - в центре круга. Любая точка полюсной фигуры определяет ориентацию кристаллической решетки относительно выбранных направлений НН - НП - ПН.

При построении полюсные фигуры при съемке на просвет или отражение отличаются точкой начала отсчета.

За начальную точку при построении полюсной фигуры методом на отражение принимают точку НП. В случае построения ее методом съемки на просвет за начало принимается точка на периферии полюсной фигуры, соответствующая направлению ПН.

Образец в начальном положении устанавливается на столике таким образом, чтобы направление нормали к образцу находилось в плоскости, включающей падающий и отраженный от образца пучки. Этот угол принимается за нулевое положение (α=0). Установим угол 2θ между осью падающего пучка и осью счетчика отраженных импульсов. При этом на счетчик попадают отраженные импульсы, количество которых пропорционально общей площади зерен, выходящих на поверхность образца исследуемой плоскостью (hkl), имеющей межплоскостное расстояние d, см. (7.1).

В этом положении (α=0) образец поворачивают на угол 360 вокруг своей оси (один полный оборот) для того, чтобы вся совокупность плоскостей {hkl} могла дать отраженный сигнал от падающего на образец пучка. При этом записывающее устройство выводит на печать график зависимости интенсивности отраженного сигнала от угла поворота I(), рис. 7.4.

П

Рис. 7.4. Текстурная кривая{200}, полученная съемкой на отражение

кривая 1интенсивность отражения от текстурованного образца;2 интенсивность отражения от бестекстурного эталона

осле первого полного круга при α=0 образец поворачивают на угол α=2,55и вновь проворачивают вокруг своей оси на 360, продолжая записывать графикI(β) для второго круга. Эту процедуру продолжают до углов разворота образца α=7090. Обычно образец разворачивают до углов α=70, поскольку при больших углах могут возникать большие искажения ввиду того, что под падающий пучок рентгеновского излучения попадают торцевые участки исследуемого образца.

Для определения интенсивности отражения рентгеновских лучей от исследуемого текстурованного образца, представленной на рис. 7.4 в виде кривой 1, проводят такую же съемку для бестекстурного образца (эталона). Бестекстурный образец получают обычно из металлического мелкодисперсного порошка, полученного из того же материала, что и исследуемый текстурованный образец. Порошок хорошо перемешивают, добавляют связующее вещество (глицерин или технический вазелин), вновь перемешивают, а затем заполняют полученной смесью специальную стеклянную кювету. Исследование интенсивности отражения в зависимости от углов α и β должно на эталоне показать постоянное значение I(β)=const. Эту величину принимают за единицу отражения (кривая 2 на рис. 7.4). Интенсивность отражения I(α, β) от текстурованного образца считают в этих единицах отражения.

Для анализа текстуры исследуемого образца на стандартную стереографическую проекцию для какой-либо плоскости (например, для плоскости {001} на рис. 7.2) при помощи спирали наносят интенсивность отражений I(α, β). Шаг спирали соответствует шагу поворотов по углу α. За исходную точку отсчета, как было указано, принимают направление прокатки (НП).

Построение полюсной фигуры по сути напоминает построение топографической карты, на которой высоты гор или холмов показаны не цветом, а линиями, определяющими некоторую высоту. Например,  100 м  - линия, показывающая высоту ландшафта 100 м над уровнем моря. Аналогичные линии присутствуют на полюсной фигуре вокруг некоторых полюсов, например, вокруг (111). Число  10  показывает интенсивность отражений в данной плоскости от исследуемой плоскости, измеренную в единицах отражений от бестекстурного эталона. Чем больше это число, тем выше интенсивность текстуры.

Стереографическая проекция каких-либо кристаллографических плоскостей с нанесенными на нее интенсивностями отражений исследуемой плоскости от бестекстурного эталона называется полюсной фигурой. Если съемка текстурной кривой I(α, β) производится путем поворота образца на углы α,  и полюсная фигура строится в координатах внешних осей образца, то такие полюсные фигуры называются прямыми (ППФ). Таким образом, в результате съемки прямых полюсных фигур определяют углы нормалей к кристаллографическим плоскостям (например, к плоскостям {111}) относительно внешних осей образца (при прокатке это НН, НП и ПН). Строят обычно 2 – 4 ППФ для разных отражающих плоскостей (для ГЦК – металлов это плоскости (111), (100), (110) и (311)).

Обратная полюсная фигура - это стандартная проекция, представляющая собой распределение ориентировок внешних осей образца (при прокатке строят обычно ОПФ НН) относительно стандартных осей кристаллической решетки (для ГЦК – плоскости {100}). При съемке обратных полюсных фигур положение счетчика по отношению к первичному рентгеновскому пучку не остается постоянным. Определяют кривую распределения интенсивности отраженного от образца рентгеновского пучка при непрерывном изменении угла в. Снимают профиль ряда линии HKL для образ­ца и эталона и определяют интегральную интенсивность каждой линии из условия пропорциональности ей площади диаграммы, ограниченной кривой распределения интенсивности и линией фона.

Рис. ОПФ (цифры 1 – 4 –полюсная плотность в интенсивностях эталона)

Расшифровка прямых полюсных фигур. Кристаллические ориентировки лис­тового материала часто настолько сложны, что описать текстуру словами трудно, а иногда и невозможно. Полюсные фигуры наиболее совершенно и точно воспроизводят текстуру. Представление текстуры при помощи прямых полюсных фигур является достаточно информативным. Однако для получе­ния необходимой информации относительно свойств материала с данной тек­стурой или особенностей формирования полученной текстуры необходимо выполнить расшифровку полюсной фигуры и интерпретировать полученные данные.

Основные пути расшифровки полюсной фигуры - это описание ее либо с помощью идеальных ориентировок и рассеяния вокруг них, либо при помощи полных или неполных аксиальных текстур, либо при помощи функций распределения ориентировок, позволяющих с большой достоверностью строить обратные полюсные фигуры.

Если применяется метод расшифровки с помощью идеальных ориенти­ровок и не удается полностью описать текстуру с помощью одной ориенти­ровки, находят вторую или несколько идеальных ориентировок.

Для определения идеальной ориентировки накладывают экспериментальную полюсную фигуру {Ш} на стереографическую проекцию монокри­сталла и совмещают полюса (hkl) с максимумами полюсной плотности таким образом, чтобы центры их совпадали.

Однако при такой расшифровке всегда остается элемент неопределен­ности вследствие влияния наложения ориентировок. Поскольку каждая ори­ентировка описывается не одним, а несколькими полюсами не всегда воз­можно понять, какой полюс относится к той или иной ориентировке.

Для повышения достоверности полученных данных выполняют съемку полюсных фигур для нескольких линий (HKL). Трудности расшифровки полюс­ных фигур приводят к тому, что описанные в литературе идеальные ориенти­ровки часто являются компромиссными. Такие описания недостаточно точно и достоверно описывают полученную текстуру.

На рис. 1.4 приведены полюсные фигуры {200}, показывающие поло­жения полюсов {001} для идеальных ориентировок текстур прокатки.

Рис. 1.4. Полюсные фигуры {200} идеальных ориентировок типичных

текстур прокатки

Более исчерпывающим и совершенным способом описания текстуры является вычисление по нескольким прямым полюсным фигурам функций

16

распределения ориентации кристаллитов (ФРО) на основе методов теории вероятности. С помощью функций распределения ориентации можно одно­значно описать не только основные ориентировки текстуры, но и области рассеяния ориентировок вокруг максимумов плотности вероятности в ориен-тационном пространстве. Метод был предложен независимо Кое (Рое) /1.253/ иВип§е(Бунге)/1.254/.

ФРО (например, Р((р\, (р , (р г) по Bunge) выражалась через серию обоб­щенных сферических гармоник, учитывающих данные исследования конкретной текстуры. Каждой ориентировке текстуры соответствует точка в пространстве Эйлера. На рис. 1.5 представлено расположение ориентации в Эйлеровом пространстве по Bunge.

Рис. 1.5. Расположение ориентации в пространстве Эйлера при расчету

по методу Випgе

Сопоставление полюсных фигур рис. 1.4 и ФРО рис. 1.5 показывает, что большинство важных ориентировок текстуры можно представить с по­мощью некоторого сечения Эйлерова пространства. Например, на рис. !.6, 6 показано положение идеальных ориентировок в сечении (р ₂ = 45° этого про­странства, где видно большинство практически важных ориентировок, по-

17

люсные фигуры которых приведены на рис. 1.4.

На рис. 1.6, а представлено сечение Ф = 45° по Кое, а на рис. 1.6, б -сечение ф ₂= 45° по Вип§е. Рис. 1.5 и 1.6 могут быть непосредственно ис­пользованы для расшифровки приведенных ниже данных исследования тек­стуры, которые одни экспериментаторы вычисляли по Вшт§е, а другие - но Кое.

Рис. 1.6. Положение идеальных ориентировок текстур, типичных для железа, в сечениях Ф = 45° (а) и (р ₂ = 45° (б) пространства Эйлера, получен­ных по методам Кое (а) и Вип§е (б) соответственно

В качестве примера преобразования информации, получаемой из по­люсных фигур, приведем стандартную программу, разработанную С.Ф. Кур-тасовым на основе метода Бунге /1.255/.

Ориентацию кристаллита § определяем с помощью системы координат, предложенной Вип§е и определяемой углами (р_}, (р, <р±. Эти углы соответст­вуют повороту осей элементарной ячейки кристаллической решетки относи­тельно системы координат, связанной с осями образца, для прокатанного листа как правило НП, НН и ПН (направление прокатки, нормаль к плоско-

18

сти прокатки и поперечное направление при прокатке соответственно).

Если весь объем кристаллического образца обозначить через V, то вы­ражение

позволяет определить трехмерную функцию распределения кристаллографи­ческих ориентировокД^ь^»,^) или ФРО.

После разложения ФРО в ряд по обобщенным сферическим функциям, учитывающим как симметрию кристаллической решетки, так и симметрию образца, получаем:

где Т}^пп((р\,(р,(р^) - обобщенные сферические функции; С/""⁷ - коэффициен­ты разложения, которые вычисляются по результатам съемки эксперимен­тальных неполных полюсных фигур (ЭПФ).

Теперь мы можем непосредственно использовать ФРО, где каждой точке ориентационного пространства соответствует определенная ориента-ционная плотность. Можем проинтегрировать ФРО либо по углу вращения вокруг направления в образце, совпадающее с кристаллографическим на­правлением <пк!>/, - получим теоретическую полюсную фигуру <Ы<_1>, (ТПФ), либо по углам поворота кристаллографических осей вокруг направ­лений НП, НН и ПН - получим обратные полюсные фигуры (ОПФ).

Рис. 1.7. Процесс анализа текстуры: ЭПФ - экспериментальная полюс-

1-9

Процесс расчета может быть представлен в виде схемы (рис. 1.7):

нал фигура

На рис. 1.8... 1.10 приведены результаты расчета ФРО по трем непол­ным полюсным фигурам {110}, {200} и {211} для случая броневой стали /1.12, 1.13/.

Рис. 1.8. ФРО для холоднокатаной броневой стали СПС-43. ср\ = сопз1, шаг 0,5 б/о (эталон)

Рис. 1.9. Сечение ФРО (рис. 1.8), (р\ = 90 для стали СПС-43

20

Рис. 1.10. Расчетная обратная полюсная фигура стали СПС-43.

Шаг 0,3 б/о

Полная математическая обработка может быть найдена в работах Бунге и др. /1.256... 1.259/. Три угла Эйлера, использованные Бунге для описания поворотов ф\, р, д>2, тогда как Рое назвал углы Т, 0 и Ф соответственно /1.206/.

Согласно Бунге, ФРО может быть выражена как серия обобщенных сферических гармоник в форме:

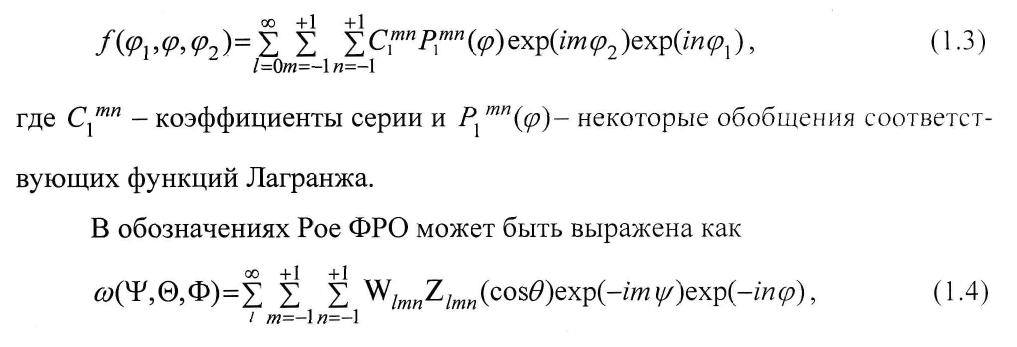
где ^1_тп- коэффициенты серии и 2/_ШЙ (со5<9) - обобщение соответствующих функций Лагранжа, так называемые расширенные полиномы Якоби /1.260/. Между углами Рое и Бунге следующее соотношение:

Хотя два метода эквивалентны, имеются небольшие различия в дета­лях, которые обсуждаются в работе /1.261/.

Однако этот метод подобно методу Топез апё \Уа1кег страдает тем не­достатком, что описание исходной структуры чересчур упрощено и отсутст­вуют количественные корреляции. Становится очевидным, что точное пред­сказание текстур превращения требует более полного описания исходных текстур, чем это возможно через идеальные ориентировки. ФРО лучше соот­ветствует этой цели и при знании точного кристаллографического соотноше­ния между исходной и конечной фазами возможно рассчитать ориентацию конечной фазы с использованием соответствующей матрицы превращения.

Кое /1.262/ показал, что, когда текстура представлена с помощью ФРО, исходный набор коэффициентов серий разложения М^/_т„ (1.4) может преобра­зоваться в новый набор коэффициентов серий разложения ^'/_т„ для ФРО, получающейся в результате превращения фазы при условии, что известны углы Эйлера а, Д у, связывающие кристаллографические оси исходной и ко­нечной структур. При этом коэффициенты \У^/_ти текстуры полученной струк­туры связаны с коэффициентами \У/_т„ исходной текстуры выражением:

Если, при отсутствии физических ограничений, имеет место беспоря­дочный характер выбора вариантов, уравнение (1.6) может быть переписано следующим образом:

Основываясь на уравнении (1.7), Вау1ез и др. /1.263/ написали компью­терную программу для вычисления коэффициентов текстуры превращения МУ'/ши из коэффициентов экспериментально определенной текстуры XV/,,,,, для

случая у—>а фазового превращения. Форма превращения описывается опре­делением полярных углов инвариантной оси и угла поворота вокруг этой оси. Для этого расчета использовано ориентационное соотношение К-8 и было принято, что все 24 варианта превращения равновероятны. Подобный метод использован Розр1есп и др. /1.264/ с использованием обозначений Bunge /1.257, 1.258/ для объяснения текстуры бейнита, образованного из го­рячекатаного аустенита.