Оглавление

Лекция 13 111

5. СТРУКТУРА ДЕФОРМИРОВАННОГО МЕТАЛЛА. 111

МЕХАНИЗМЫ ДЕФОРМАЦИИ И УПРОЧНЕНИЯ 111

5.1. Трехмерная сетка дислокаций и её поведение при деформации 111

Поведение сетки дислокаций при малых напряжениях 112

Поведение сетки дислокаций при больших напряжениях 114

Релаксация напряжений при низких температурах 115

5.2. Скопление дислокаций 117

5.3. Дислокационная стенка 117

5.4. Дислокационные сплетения, клубки и жгуты. Ячеистая и блочная структуры 121

Дислокационные сплетения 121

Формирование блочной структуры 122

5.5. ФОРМИРОВАНИЕ СТРУКТУРЫ ПРИ БОЛЬШИХ ДЕФОРМАЦИЯХ. ОБРАЗОВАНИЕ ПЕРЕОРИЕНТИРОВАННЫХ ОБЛАСТЕЙ И РОТАЦИОННАЯ ПЛАСТИЧНОСТЬ 122

Лекция 14 124

5.5.1. Полосы скольжения 124

5.5.2. Полосы сброса 126

5.5.3. Фрагментация 131

5.6. Модель «хищник  жертва» для описания превращений дефектов кристаллического строения при пластической деформации 135

Лекция 15 137

5.7. ИЗМЕНЕНИЕ СВОЙСТВ МЕТАЛЛА ПРИ ОБРАЗОВАНИИ ФРАГМЕНТИРОВАННОЙ СТРУКТУРЫ 137

5.8. Двойникование – особый вид переориентации в кристаллах 139

5.9. ФОРМИРОВАНИЕ СТРУКТУРЫ ПРИ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ МЕТАЛЛА НА ПРИМЕРЕ ХОЛОДНОКАТАННОГО РЕНИЯ 142

Итоги главы 149

Лекция 13

5. Структура деформированного металла. Механизмы деформации и упрочнения

Рассмотрим некоторые дислокационные конфигурации, которые возникают в металле при пластической деформации или термической обработке

5.1. Трехмерная сетка дислокаций и её поведение при деформации

Трехмерная дислокационная сетка представлена на рис. 5.1. Она образуется обычно при малых степенях деформации. Все пространство кристалла более или менее равномерно заполнено дислокационными отрезками со средней длиной

,

где ρ – общая плотность дислокаций. Эти отрезки соединены концами в тройные и четверные дислокационные узлы, закрепляющие их. В целом картина напоминает скомканную паутину.

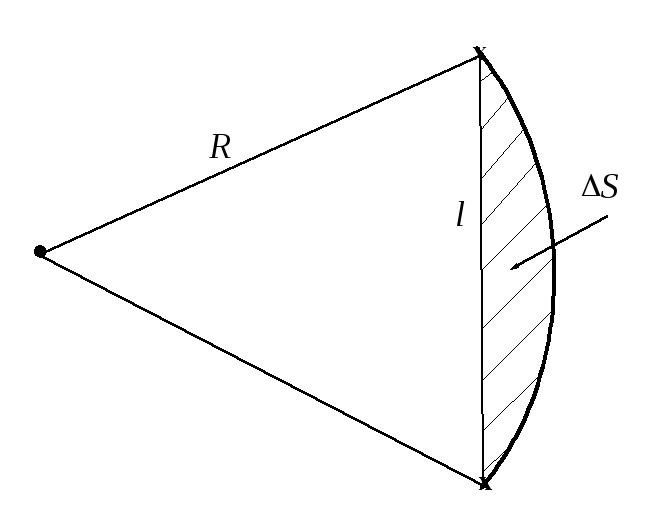
Рис. 5.1. Трехмерная дислокационная сетка в рении, ×30000	Рис. 5.2. Элементарная пластическая деформация за счет прогибания звена трехмерной дислокационной сетки (заштриховано)

В силу случайного характера распределения дислокаций поле дальнодействующих напряжений близко к хаотическому. В этом случае каждый из отрезков дислокации может двигаться почти независимо от других.

Пусть все звенья сетки имеют одинаковый размер, равный среднему

,

где ρ – плотность дислокаций.

Поведение сетки дислокаций при малых напряжениях

При малых внешних напряжениях ( меньше критического – формула (3.30) – условие действия источника Франка - Рида) величиной

вся сетка будет устойчива, но каждое ее звено прогнется, образовав дуги со средним радиусом кривизны (рис. 5.2) (см.формулу (3.29), в которой обозначено =2)

.

Для малых напряжений σ, при которых R>>l, площадь сегмента ΔS, по которой прошло скольжение от прогиба дислокации (то есть пластическая деформация, которая в данном случае будет обратимой и при снятии напряжений, дислокации вернутся в исходное положение), равна

(5.1)

Предельное значение площади при R=Rmin=l/2 равно

ΔS=πR²/2=πl²/8.

Считается, что пластическая деформация в объеме за счет смещения всех N = ρ/l звеньев (в единице объёма) составит

(5.1а)

Таким образом, после приложения малых напряжений  тело деформируется:

- сначала упруго от смещения атомов

ε_у= /G или σ/E

в зависимости от вида напряженного состояния,

- а затем пластически от прогиба дислокаций на величину

, (5.1б)

Где коэффициент α = сonst<1 зависит от функции распределения дислокаций по длинам в сетке. Очевидно, что и для других дислокационных структур в области малых напряжений будет иметь место пластическая деформация того же порядка. В нулевом приближении эта деформация не зависит от ρ (как ясно из формул). Эта пластическая деформация обратимая.

Пластическая деформация требует большего времени, чем упругая, поэтому суммарная зависимость

ε_об=ε_у+ε_п =f(t)

от времени будет иметь два участка, как показано на рис. 5.3.

Главной особенностью пластической деформации в области малых напряжений является ее обратимость. Действительно, после снятия нагрузки дислокации под действием сил линейного натяжения возвращаются в исходные положения, совершая ту же пластическую деформацию в обратном направлении. Таким образом, вся деформация ε=ε_у+ε_п­ ведет себя как квазиупругая, но требующая для своего установления значительно большего времени, чем упругая. В соответствии с этим свойством полную обратимую деформацию ε_об принято описывать упругим модулем (Е_р или G_р), который в отличие от обычного модуля упругости называется релаксирующим.

Тогда, например, при растяжении (с учётом формулы (5.1б))

. (5.2)

Очень важно, что обратимая деформация будет иметь такую же величину для дислокационных структур всех типов, так как она отличается от упругой только коэффициентом α, который не может сильно изменяться. Движение дислокаций термоактивированное, поэтому время установления обратимой квазиупругой деформации будет тем больше, чем ниже температура.

а)	б)
Рис. 5.3. Зависимость квазиупругой деформации от времени после приложения нагрузки t<tσ и после разгрузки t≥tσ (а) и функция распределения числа звеньев дислокационной сетки по их длинам l (б)

Очень важно, что обратимая деформация будет иметь такую же величину для дислокационных структур всех типов, так как она отличается от упругой только за счет коэффициента α, который не может сильно изменяться. Движение дислокаций термоактивированное, поэтому время установления обратимой квазиупругой деформации будет тем больше, чем ниже температура.