Торможение дислокаций частицами другой фазы.

Пусть при движении дислокация упирается в ряд частиц второй фазы. Частицы другой фазы могут состоять совсем из другого материала, чем матрица (например, интерметаллиды, карбиды или нитриды, образуемые легирующими элементами), или являться соединением атомов матрицы с примесными или легирующими атомами (карбиды, нитриды, интерметаллиды). И в том, и в другом случае постоянная кристаллической решетки включения обычно отличается от основной, что делает невозможным переход дислокации из матрицы во включение.

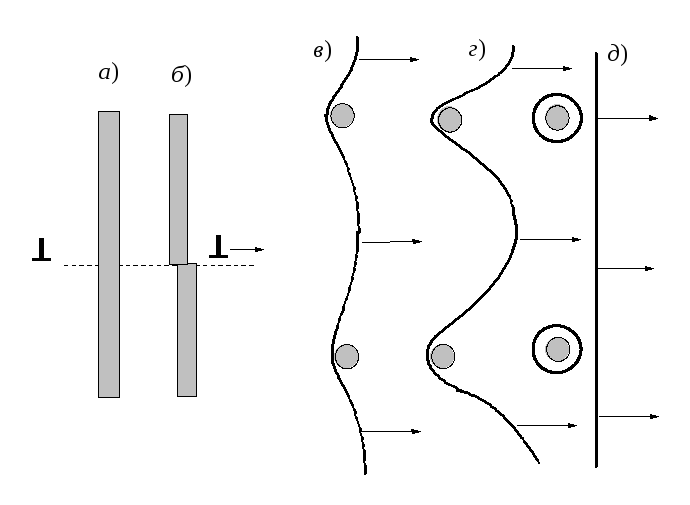
Для преодоления частиц выделений второй фазы у дислокации есть только две возможности – рассечение и огибание (рис. 3.36).

При огибании происходит взаимодействие дислокаций и включений, аналогичное работе источника Франка-Рида  после прохождения дислокации на включении остается по дислокационной петле.

При рассечении верхняя часть включения смещается относительно нижней на вектор Бюргерса основной решетки b, который не равен межатомному расстоянию включения. Потому восстановление сплошности после прохождения дислокации невозможно, и образуется плоский дефект типа трещины, включение перерезается. Поверхностная энергия такого дефекта будет:

, (3.61)

где S – площадь поперечного сечения включения; γ_s – удельная поверхностная энергия разреза, примерно равная удельной энергии свободной поверхности;  теоретическая прочность материала включения.

Рис. 3.36. Способы преодоления дислокацией нитевидных включений второй фазы: а и б – последовательные стадии рассечения (вид сбоку); в-д – последовательные стадии огибания

Работа перемещения дислокации при рассечении включения

A=τbd2r,

где d − среднее расстояние между включениями, равное длине отрезка дислокации; 2r − путь дислокации при рассечении включения, r − радиус включения.

Рассечение становится энергетически выгодным при выполнении условия AW:

. (3.62)

Таким образом, напряжения, достаточные для рассечения включения зависят от типа включения, а именно − его теоретической прочности τ_вкл, а также от размера включения r и расстояния между ними d.

Огибание препятствий происходит в соответствии с условиями работы источника Франка–Рида:

. (3.63)

Определим среднее расстояние между включениями при концентрации легирующего элемента f, если частицы имеют форму сферы радиусом r_вкл и объемом v_вкл. Пусть N₀  число атомов металла, N_вкл  число атомов примесного или легирующего элемента, составляющих включение. Тогда

N_вкл = N₀ f ,

число включений

,

где N₁  число атомов в одном включении, , а  параметр решетки материала включения. При , гдеа  параметр решетки основного материала,

.

Среднее расстояние между включениями

.

С учетом последнего выражения формулу (3.63) можно переписать в виде

. (3.64)

Таким образом, при помощи рассмотренной модели взаимодействия примесей с дислокациями видно, что упрочнение за счет недеформируемых включений второй фазы определяется в основном их дисперсностью (при постоянной концентрации обратно пропорционально размеру включения). Концентрация включений второй фазы при постоянном размере влияет на упрочнение в значительно меньшей степени (т.к. корень кубический). То есть эффективнее упрочнение за счёт измельчения второй фазы, а не за счёт увеличения концентрации (объёмной доли второй фазы).

Сравнивая (3.62) и (3.63), видим, что огибание происходит при значительно меньших напряжениях, чем рассечение. Насколько вероятно рассечение включений? Во-первых, способ преодоления включений зависит от их количества и дисперсности. Сначала, очевидно, преимущественным механизмом будет огибание, как требующее меньших напряжений . Однако, по мере увеличения плотности дислокаций и «зарастания» дислокациями пространства между включениями внешние напряжения, необходимые для осуществления пластической деформации, возрастают и могут достичь значений, определяемых соотношением (3.62). При этом должно произойти разрушение включения.

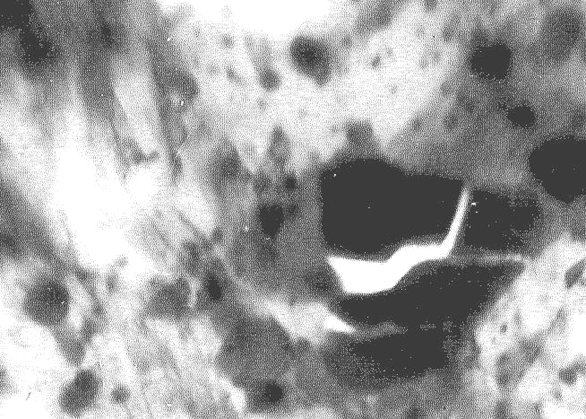
Рассмотрим схему на рис. 3.37, иллюстрирующую взаимодействие включения с «дислокационной шубой», образованной при огибании включения дислокациями. Взаимодействие происходит в плоскости рис. 3.36,в при образовании нескольких петель на одном из включений.

Видно, что «дислокационная шуба» на включении состоит из нескольких дислокаций, причем по противоположные стороны включения расположены отрезки дислокаций противоположного знака, представляющие собой скопления. На головных дислокациях суммируются напряжения от всех дислокаций скопления, поэтому на включение действуют напряжения среза, многократно превышающие напряжения от отдельных дислокаций, рассчитываемые по (3.62). Это значительно повышает вероятность разрушения включения срезом.

Во-вторых, как видно по (3.62), вероятность рассечения включения повышается с уменьшением теоретической прочности включения . Если>^*, где ^*  теоретическая прочность основного металла, то включения оказывают упрочняющее действие; при <^* присутствие включений может вызвать хрупкость металла из-за острых микротрещин, возникающих при рассечении включения. Такие микротрещины являются мощными концентраторами напряжений.

Рис. 3.37. Рассечение включения при взаимодействии с «дислокационной шубой»: а, б  схема взаимодействия; в  рассечение включения в бериллии

в)

Примерами негативного влияния включений являются интерметаллиды FeBe₁₁ и AlFeBe₄ и оксиды BeO в бериллии, интерметаллиды Cr₃Si и Cr₂Al в хроме, рис. 3.37,в. При <^* включения разрушаются уже при малых степенях деформации, а образованные при этом микротрещины могут вызвать макроразрушение образца.