3.6. Энергия дислокации

Кристалл, содержащий дислокацию, обладает собственной энергией W_д, большей, чем энергия W_и идеального кристалла из такого же числа атомов. Избыток энергии ΔW=W_дW_и называется собственной энергией дислокации. Вычислим собственную энергию прямолинейной винтовой дислокации ΔW_в≡ W_в, проходящей по оси цилиндрического кристалла радиусом R и длиной L (рис.3.14). В элементе объема dV(r), расположенном на расстоянии r от оси дислокации, согласно формуле (3.14) создаются напряжения τ(r) =. Согласно линейной теории упругости это означает, что объем

dV(r)=rddrdz

обладает избыточной упругой энергией

. (3.16)

Рис. 3.13. Характер напряжений, создаваемых краевой дислокацией	Рис. 3.14. Выбор элемента объема при вычислении энергии винтовой дислокации

Полная энергия дислокации получится из (3.16), если dW(r) проинтегрировать по всему объему кристалла:

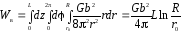. (3.17)

Формула (3.17) учитывает энергию упругих напряжений, действующих в полом цилиндре с радиусами r₀ и R, но не учитывает энергии ядра дислокации, т.е. энергии упругих напряжений при r<r₀. В ядре дислокации методы механики сплошной среды неприменимы, поэтому оценка энергии ядра дислокации носит приближенный характер. Для оценочных расчетов принимают

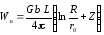, (3.18)

где Z учитывает энергию ядра дислокации, причем Z≈1÷3.

Оценки вклада дальнодействующих напряжений в энергию дислокации показывают, что W_в зависит от радиуса R, т.е. от размера контура, по которому выполняют интегрирование (3.17). Радиус интегрирования R часто называют «радиусом экранирования» напряжений от дислокации. В выборе R существует некоторый произвол, поскольку при R энергия дислокации бесконечно велика, а при Rr₀ W_в0. В связи с этим приближенно принимают

R_min≈100r₀≈500·10⁻¹⁰ м, а R_max≈ 0,1 мкм = 10⁻⁷ м,

что равно среднему расстоянию между дислокациями.

Среднее значение логарифма в (3.18) составляет (подставляем среднее геометрическое R=R_ср=R_minR_max)

.

С учетом энергии ядра Z=1÷3 можно принять упрощенное выражение для оценки энергии винтовой дислокации

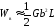. (3.19)

Энергия краевой дислокации W_к вычисляется совершенно аналогично, только из-за большего числа компонентов напряжения расчеты более громоздки. Результат вычислений имеет вид

, (3.20)

где  коэффициент Пуассона.

Можно написать общую формулу для энергии дислокации W_д:

, (3.21)

где K = 1 для винтовой, К = 1 – ξ для краевой и 1–ξ< K<1 для смешанной дислокации; τ* - напряжение сдвига в идеальном кристалле (см.гл.1).

Таким образом, можно сделать следующие выводы:

1. Энергия дислокации пропорциональна ее длине.

2. По порядку величины энергии различных дислокаций совпадают.

3. Энергия дислокации даже длиной в одно межатомное расстояние (L = b) велика и соизмерима с энергией связи атомов:

.

При G ≈ 30 ГПа и а = 3ּ10^–10 м 2,53 эВ.

4. Энергия дислокации пропорциональна b² – квадрату ее вектора Бюргерса. Если проследить вывод формулы (3.21), то эта зависимость становится очевидной: W_д ~ τε – энергия пропорциональна произведению напряжений на деформацию, где τ ~ b и ε = τ/G.

5. Вклад в энергию дислокации от дальнодействующих напряжений, пропорциональный lnR/r₀ = 5÷10, всегда больше, чем вклад от области ядра Z≈l÷3.