Расщепление дислокаций

Кроме объединения нескольких дислокаций в одну, возможна и обратная реакция расщепления одной дислокации на две или более. Если геометрия решетки допускает расщепление дислокации с вектором Бюргерса b на две с векторами b₁ и b₂, то рассуждения, аналогичные предыдущим, приведут к формуле энергетической выгодности данного процесса:

или .(3.38)

Обычно дислокации имеют наименьший из возможных векторов Бюргерса. Действительно, пусть имеется дислокация с вектором Бюргерса B=2b. Тогда для нее всегда выгодна реакция расщепления В→b+b, так как

. (3.39)

Энергетическое условие слияния или расщепления дислокаций является необходимым, но не достаточным условием, поэтому дело с рассматриваемым взаимодействием дислокаций обстоит сложнее. Используем для анализа энергетической выгодности слияния дислокаций условие Гельмгольца.

Пусть в исходном состоянии система имеет энергию

в конечном

,

а изменение энергии

,

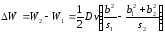где v  объем системы, s  площадь сечения дислокационной трубки, по которой интегрируют напряжения для определения энергии дислокации. Совершенно необязательно, что s = const.

Если слияние дислокаций выгодно при выполнении условия Гельмгольца, то при слиянии должно выполняться соотношение

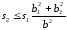. (3.40)

Промежуточные выводы:

1. Дислокация характеризуется двумя векторами – единичным вектором направления оси дислокации l и вектором Бюргерса b, направление которого характеризует направление смещений вблизи дислокации, а величина – мощность дислокации.

2. Дислокация является источником мощных и медленно спадающих упругих напряжений.

3. Пластическая деформация происходит в основном за счет перемещения дислокаций в теле.

4. Дислокация имеет относительно высокую энергию порядка 1/2 Gb³ на одну атомную плоскость [и не может образоваться за счёт тепловых флуктуаций].

5. Под действием внешних напряжений дислокации движутся так, что при этом площадь, по которой прошло скольжение, увеличивается.

6. Дислокации могут размножаться.

7. Дислокации могут вступать в реакции – объединяться или разделяться.

3.13. Пересечение дислокаций

Пусть имеются две дислокации в различных плоскостях скольжения (рис.3.33): краевая АБ с осью вдоль Oz в плоскости скольжения x0z и неподвижная дислокация ВГ с осью вдоль Оу. После прохождения дислокации АБ через весь кристалл его верхняя часть смещается относительно нижней на величину вектора Бюргерса b вдоль оси Ох, в том числе и часть ВВ' дислокации ВГ. Но так как линия дислокации не может прерываться внутри кристалла, то между нижней ГГ' и верхней ВВ' частями дислокации образуется двойной излом В'Г' (винтовой участок).

I. Для краевых дислокаций возможны два варианта:

1. Этот излом будет перегибом, если вектор Бюргерса дислокации ВГ направлен вдоль Ох: b_ВГ=b_x,

2. и ступенькой, если b_ВГ=b_z (рис. 3.33,б) (экстраплоскость всегда перпендикулярна вектору Бюргерса).

II. Если дислокация АБ была винтовой с b=b_z, то, наоборот:

1. при b_ВГ=b_x получается ступенька,

2. а при b_ВГ=b_z – перегиб (рис.3.33,в).

Рис. 3.33. Пересечение дислокаций: а – движение краевой дислокации АБ в плоскости xOz с вектором Бюргерса b=b_x навстречу неподвижной дислокации ВГ; б – результат прохождения дислокации АВ – сдвиг верхней полуплоскости на b и образование двойного излома В′Г′ на дислокации ВГ; в – аналогичная картина после прохождения винтовой дислокации АБ (с вектором Бюргерса b=b_z)

Радиус действия напряжений от ступеньки (или перегиба) высотой b порядка нескольких b (R = (2÷4)b). Подставив это значение в формулу для энергии дислокации, видим, что энергия каждой из дислокаций после пересечения увеличивается на величину

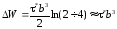. (3.49)

Следовательно, пересечение дислокаций требует дополнительных затрат энергии и приводит поэтому к упрочнению кристалла. Внешнее напряжение совершает работу при перемещении дислокации на Δx=b, равную

А = τb²L, (3.50)

где L  длина этой дислокации.

Действительно, так как дислокации перпендикулярны, то их ядра, а следовательно, и область больших напряжений далеки друг от друга, за исключением соприкасающихся при пересечении участков. Поэтому основной вклад в энергию взаимодействия пересекающихся дислокаций, в отличие от взаимодействия параллельных дислокаций, вносят ядра дислокаций. Расстояние, на котором существенно взаимодействие дислокаций, порядка b: Δx ≈ b.

Таким образом, условие энергетической выгодности пересечения дислокаций приобретает вид

А = τb²L > ΔW ≈ τ^*b³ или τ > τ^*b/L, (3.51)

(где * - теоретическая прочность на сдвиг), что очень похоже на условие работы источника Франка – Рида.

При длине дислокации

L<b

пересечение дислокаций энергетически невыгодно (они тормозятся друг на друге, т.е. не могут разойтись).

Таким образом, пересекающиеся дислокации взаимодействуют в основном только за счет ядер и на малых расстояниях, когда их ядра соприкасаются. Пересечение дислокаций приводит к увеличению их длины и, следовательно, требует дополнительных затрат энергии. Поэтому перемещение подвижных дислокации через неподвижные (дислокации «леса») требует добавочных напряжений, т. е. приводит к упрочнению тела.