3.11. Дислокационные реакции

Рассмотрим дислокационные реакции объединения двух или более дислокаций в одну и расщепление дислокации (разделение одной дислокации на две или более). Начнем с примера простейшей дислокационной реакции между двумя параллельными краевыми дислокациями(рис.3.27).

Рис. 3.27. Дислокационная реакция между двумя параллельными краевыми дислокациями с векторами Бюргерса b₁ и b₂, в результате которой получается дислокация с вектором Бюргерса b: а – схема объединения дислокаций (АВ и ВС – плоскости скольжения); б – треугольник из векторов Бюргерса

Пусть обе дислокации двигались к точке В: первая - с вектором Бюргерса b₁ в плоскости со следом АВ, вторая - с вектором Бюргерса b₂ в плоскости СВ. При их встрече в точке В происходит слияние их осей вдоль прямой, перпендикулярной плоскости АВС. Вектор Бюргерса дислокации, получившейся в результате такой дислокационной реакции, определяется из условия

b₁ + b₂ = b. (3.34)

Необходимо помнить, что невязка контура Бюргерса b является вектором, поэтому сложение векторов Бюргерса следует выполнять по правилу параллелограмма или треугольника (см. рис. 3.27,б). Рассмотрим энергетическую выгодность такой реакции в приближении линейного натяжения. Энергия дислокаций 1 и 2 в исходном состоянии (когда расстояние между ними велико и вкладом в энергию от их взаимодействия можно пренебречь) равна:

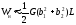. (3.35)

В конечном состоянии

.

Следовательно, слияние дислокации энергетически выгодно при условии

или

, (3.36)

т. е. если угол между векторами b₁ и b₂ острый (α<π/2).

В приближении линейного натяжения условие дислокационной реакции всегда будет иметь вид (3.36). Для получения более точного результата надо учесть зависимость энергии от угла между l и b (если дислокации не краевые).

Если в реакцию вступают п параллельных дислокации 1, 2, ..., п с вектором Бюргерса b₁, b₂, ..., b_n, то аналогичный расчет для энергетической выгодности процесса даст

. (3.37)

Частным случаем дислокационной реакции является аннигиляция двух дислокации противоположного знака, при которой b₁=–b₂ и b=b₁+b₂=0. Для краевых дислокации аннигиляция означает объединение двух полуплоскостей в одну целую плоскость. При этом они исчезают и восстанавливается правильная решетка.

Рис. 3.28. Реакция между пересекающимися дислокациями: а – две пересекающиеся винтовые дислокации образуют участок с вектором Бюргерса b_3, на котором прошла реакция; б – треугольник для определения b₃; в – образование гексагональной сетки из винтовых дислокаций

На рис. 3.28 показан случай другой реакции: две винтовые дислокации с , пересекающиеся под углом друг к другу. Если

,

то энергетически выгоден изгиб дислокационных линий около точки пересечения и образование участка, на котором происходит дислокационная реакция. Когда , этот участок также будет винтовым (см. рис.3.28,б).

Если дислокации образуют сетки, состоящие из двух семейств винтовых дислокаций, и между ними будет идти реакция, то каждый узел сетки расщепится согласно схеме на рис. 3.28,а. При этом сетка из ромбической превратится в гексагональную (рис. 3.28,в). Если между линиями дислокаций в исходном состоянии был угол 120°, то все гексагональные ячейки сетки будут правильными с равными сторонами и углами по 120°. Такие гексагональные сетки часто наблюдаются в кристаллах.