
- •1.2. Кодер источника
- •2.2 Устройство декодирования помехоустойчивого группового кода
- •2.3. Циклические коды
- •2.4. Алгоритмы работы приёмников дискретных сигналов
- •3.2. Анализ помехоустойчивости узо
- •3.3. Пропускная способность двоичного симметричного канала
- •3.4. Пропускная способность каналов с рос
2.4. Алгоритмы работы приёмников дискретных сигналов
Приёмники дискретных сигналов строятся на основе результатов теории потенциальной помехоустойчивости В.А. Котельникова.
Пусть на вход приёмника поступает сумма сигнала с помехой
 .
(10)
.
(10)
Единственным
неизвестным параметром сигнала
 является переносимое им сообщение
является переносимое им сообщение ,
принимающее в бинарных системах,
случайным образом, одно из двух значений,
например,
,
принимающее в бинарных системах,
случайным образом, одно из двух значений,
например, и
и .
Априорные вероятности появления значений
.
Априорные вероятности появления значений и
и ,
то есть
,
то есть ,
полагаются известными.
,
полагаются известными.
Помеха
 представляет собой нормальный белый
шум с нулевым средним и известной
дисперсией
представляет собой нормальный белый
шум с нулевым средним и известной
дисперсией (или спектральной плотностью мощности
(или спектральной плотностью мощности ).
).
Входной
сигнал по теореме Котельникова может
быть представлен своими отсчётами,
следующими через интервал
 ,
где
,
где – максимальная частота в спектре
сигнала. Число отсчётов в одной реализации
сигнала равно
– максимальная частота в спектре
сигнала. Число отсчётов в одной реализации
сигнала равно
|
|
|
где
 – длительность битовых реализаций.
– длительность битовых реализаций.
Поскольку
интервал отсчётов
 гораздо больше интервала корреляции
гораздо больше интервала корреляции помех, то отсчёты помех, совпадающие по
времени с отсчётами сигнала, будут
взаимно независимы. Тогда многомерная
плотность распределения входной
реализации помех может быть представлена
как произведение одномерных плотностей,
то есть
помех, то отсчёты помех, совпадающие по
времени с отсчётами сигнала, будут
взаимно независимы. Тогда многомерная
плотность распределения входной
реализации помех может быть представлена
как произведение одномерных плотностей,
то есть
|
|
|
При приёме дискретных сообщений изменение формы сигнала не свидетельствует об искажении переносимого им сообщения. Поэтому от приёмника можно требовать достижения более обобщенных показателей, нежели сохранение формы сигнала, например, достижения минимальной вероятности искажения сообщений.
Если
передаётся реализация сообщения
 ,
а на приёме будет получена реализация
входного сигнала
,
а на приёме будет получена реализация
входного сигнала ,
то от приёмника можно потребовать лишь
решений, равных апостериорным вероятностям
,
то от приёмника можно потребовать лишь
решений, равных апостериорным вероятностям присутствия сообщения
присутствия сообщения в реализации
в реализации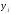 .
Поэтому критерий приёма формируется
из условия
.
Поэтому критерий приёма формируется
из условия
|
|
|
Для
бинарных систем приёмник должен принимать
решение
 ,
если
,
если
|
|
|
и
принимать решение
 ,
если неравенство не выполняется.
,
если неравенство не выполняется.
Непосредственно
вычислить вероятности
 не представляется возможным. Используя
известное равенство
не представляется возможным. Используя
известное равенство
 ,
,
переходят к критерию
|
|
( |
в
котором
 известна априори, а
известна априори, а для анализируемой ситуации. Поэтому
можно говорить о критерии
для анализируемой ситуации. Поэтому
можно говорить о критерии
|
|
( |
что
равносильно поиску максимальной
вероятности реализации помехи, равной
разности
 ,
то есть переходим к критерию
,
то есть переходим к критерию
|
|
( |
При
известной плотности распределения
помех приёмник принимает решение в
пользу сообщения
 ,
если выполняется неравенство:
,
если выполняется неравенство:
|
|
( |
или тождественное ему неравенство
|
|
( |
|
|
|
|
|
|
В
противном случае принимается решение
в пользу сообщения
 .
.
Обобщенная схема приёмника показана на рис. 8.

Рис. 8.
Каждый вариант работы должен содержать следующие этапы синтеза приёмников: а) определение отношения правдоподобия; б) вывод из отношения правдоподобия математической модели алгоритма обработки входного сигнала; в) построение функциональной схемы обработки сигнала, г) оценку помехоустойчивости данного приёмника.
3. АНАЛИЗ ПОКАЗАТЕЛЕЙ КАЧЕСТВА
КАНАЛА ПЕРЕДАЧИ ДАННЫХ
Анализ помехоустойчивости приёмников дискретных сигналов
А. Приёмник фазоманипулированных сигналов.
При
фазовой манипуляции с разносом фаз на
 сигналы
сигналы и условие (14) переходит к виду
и условие (14) переходит к виду
|
|
( |
когда
принимается решение
 .
.
Схема приемника показана на рис. 9.

Рис. 9.
Сигнал
 на рисунке означает ожидаемую реализацию
сигнала
на рисунке означает ожидаемую реализацию
сигнала .
.
Если
бы разнос фаз был равен
 ,
то сигналы
,
то сигналы и
и были бы взаимно ортогональны, например,
были бы взаимно ортогональны, например, ,
, .
Тогда схема приёмника имела бы вид,
представленный на рис.10.
.
Тогда схема приёмника имела бы вид,
представленный на рис.10.

Рис. 10.
Анализ
помехоустойчивости данных приёмников
проведём в предположении, что априорные
вероятности
 ,
сигналы используются в виде гармонических
функций с одинаковыми длительностями,
амплитудами и частотами. Различие только
в начальных фазах. Момент прихода
сигналов в пункт приёма известен точно.
,
сигналы используются в виде гармонических
функций с одинаковыми длительностями,
амплитудами и частотами. Различие только
в начальных фазах. Момент прихода
сигналов в пункт приёма известен точно.
Системы
симметричные, поэтому
 ,
где
,
где – вероятность принять
– вероятность принять ,
когда передаётся
,
когда передаётся ,
а
,
а – наоборот.
– наоборот.
Чтобы
определить помехоустойчивость приёмника,
предположим, что непрерывно передаются
символы
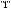 ,
а будем подсчитываться случаи приёма
ошибочных символов 0. Так оценим
вероятность
,
а будем подсчитываться случаи приёма
ошибочных символов 0. Так оценим
вероятность .
.
Пусть
 ,
реализована схема по рис. 6. Алгоритм
обработки сигнала до схемы сравнения
сводится к вычислению интеграла
,
реализована схема по рис. 6. Алгоритм
обработки сигнала до схемы сравнения
сводится к вычислению интеграла
|
|
( |
где
 – ожидаемый сигнал, имеющий амплитуду
– ожидаемый сигнал, имеющий амплитуду ,
отличающуюся от амплитуды полезной
составляющей входного сигнала из-за
некоторого затухания в среде
распространения.
,
отличающуюся от амплитуды полезной
составляющей входного сигнала из-за
некоторого затухания в среде
распространения.
После подстановки известных данных и простых преобразований находим, что
|
|
( |
где
 – энергия полезной составляющей сигнала;
– энергия полезной составляющей сигнала; – случайная величина, распределенная
по нормальному закону с нулевым средним
и дисперсией
– случайная величина, распределенная
по нормальному закону с нулевым средним
и дисперсией .
.
На выходе схемы сравнения ошибка наступит в случаях, когда будет выполнено неравенство ζ ≤ 0. Вероятность такого события

, , (16)
где ω(ζ) – плотность распределения величины ζ,
Ф(∙) – интеграл вероятности, табулированная функция.
Величина
, (17)
где  - мощность гармонического колебания
(сигнала) на входе приёмника;
- мощность гармонического колебания
(сигнала) на входе приёмника;
Т – длительность сигнала;
 - дисперсия помехи на входе приёмника.
- дисперсия помехи на входе приёмника.
Полезно проследить процесс вычисления вероятностей ошибок по рис.11, отображающему плотность распределения результатов обработки входного сигнала. Вероятность ошибочного приёма равна заштрихованной площади.
w(ζ)








0 Qt
Рис. 11.
Вывод: помехоустойчивость приёмника зависит от соотношения энергий сигнала и помехи.
При переходе к анализу схемы по рис. 10, относящейся к приёму фазоманипулированных сигналов на 90 градусов, получаем
 ,
,
 ,
т.к.
,
т.к. и
и взаимно ортогональны,
взаимно ортогональны,
где 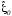 - случайная величина, независимая с
величиной
- случайная величина, независимая с
величиной ,
но имеющая одинаковый с ней закон
распределения, среднее значение и
дисперсию.
,
но имеющая одинаковый с ней закон
распределения, среднее значение и
дисперсию.
На схему сравнения поступают случайные величины
 .
(18)
.
(18)
Если неравенство нарушается, то возникает ошибка. Вероятность такого события
 ,
(19)
,
(19)
где
 .
.
Из (19) следует, что помехоустойчивость схемы с ортогональными сигналами, по сравнению со схемой приёма противоположных сигналов, эквивалентна понижению энергии сигнала в два раза.
Б. Приёмник частотно-манипулированных сигналов.
Частотная манипуляция применяется,
когда сложно обеспечить стабильность
фазы сигнала. Это обстоятельство приводит
к необходимости обработки двух координат
сигналов на каждой частоте по схеме
рис. 12.
Рис.12.
Пусть на вход приёмника приходит сигнал с неопределённой фазой φ в сумме с помехой
 .
.
Тогда в верхней ветви преобразования имеем
 ,
,
где
 - нормальная случайная величина с нулевым
средним значением и дисперсией
- нормальная случайная величина с нулевым
средним значением и дисперсией .
.
Во второй ветви
 ,
,
где
 - независимая с
- независимая с случайная величина с теми же
характеристиками.
случайная величина с теми же
характеристиками.
В третьей и четвертой ветвях получаем соответственно

где
случайные величины
 и
и взаимно независимы и независимы с
взаимно независимы и независимы с и
и ,
но имеют одинаковые с ними характеристики.
,
но имеют одинаковые с ними характеристики.
На схему сравнения поступят величины

которые
представляют собой квадраты длин
радиус-векторов точек с независимыми
и распределёнными нормально координатами,
с одинаковыми дисперсиями
 ,
но различными средними значениями.
,
но различными средними значениями.
Известно, что при нулевых средних
значениях длины векторов распределены
по закону Рэлея. Поэтому плотность
распределения случайной величины
 равна
равна
 при
при (20)
(20)
Если средние значения координат равны
Qcosφ и Qsinφ соответственно, то длина
вектора будет распределена по обобщённому
закону Рэлея. Следовательно, случайная
величина
 имеет распределение
имеет распределение
 при
при (21)
(21)
где

 - Бесселева функция мнимого аргумента
нулевого порядка.
- Бесселева функция мнимого аргумента
нулевого порядка.
Если передаётся символ “1”, то ошибка
возникает при нарушении неравенства
 .
Вероятность такого события равна
.
Вероятность такого события равна

Вычисления интегралов приводят к искомому результату
 (22)
(22)
где
 ,
,
Видно, что характер зависимости между параметрами системы и достигаемой помехоустойчивостью совсем иной, чем в схемах с фазовой манипуляцией.

 ,
, ,
(11)
,
(11) .
. ,
, ,
(12)
,
(12) ,
, .
. ,
(13)
,
(13)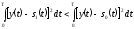 .
(14)
.
(14) ,
(15)
,
(15) ,
, ,
,