Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Куликов К.Г., Фирсов А.Н. Уравнения и методы математической физики. 2011

.pdf

Скачиваний:

423

Добавлен:

21.03.2016

Размер:

3.81 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2219 20 21 22 > Следующая >>>

Теорема 8.7.

Пусть

f (x)

– непрерывно-дифференцируемая

функция

на

отрезке a;b ,

S(x)

– дважды непрерывно=дифференцируема на a;b

S (x) 0 при x a;b . Тогда при

f (x) b

F ( ) f (x)e

i S ( x)

(i )

| O(

S (x) a

Доказательство.

Интегрируя по частям, получим:

f (x)

f (x) b

f (x)

F ( )

d (ei S ( x) ) (i ) 1

ei S ( x)

(i ) 1

ei S ( x)dx .

i S (x)

S (x) a

S (x)

Поскольку

то функция

S(x) монотонна

на отрезке a;b .

S (x) 0 ,

Делая в последнем интеграле замену переменной y S(x) , получим интеграл

вида h( y)ei y dy, который, согласно лемме Римана – Лебега стремится к нулю

при , что и дает нужную оценку для остаточного члена.

Вклад невырожденной стационарной точки

Вусловиях теоремы 8.1 содержится важное ограничение: S (x) 0 при

xa;b , то есть фазовая функция не имеет стационарных точек на отрезке

интегрирования. При наличии у фазовой функции стационарных точек асимптотика интеграла F ( ) изменяется.

Для упрощения формулировок мы будем далее полагать, что функции

являются бесконечно дифференцируемыми.

Лемма 8.3 (Лемма Эрдейи).

Пусть функция

f (x)

бесконечно

дифференцируема на отрезке 0; d

и 0. Тогда при

( ) f (x)e

f (0)e

O( 1 ).

Доказательство. Предположим вначале, что

f (x) 1.

Делая замену

переменной x t , получаем

it 2

x 2

( ) f (x)e

dt .

Первый				из интегралов, стоящих в скобках, это интеграл Френеля,
			i
равный				. Второй интеграл легко оценить, интегрируя по частям
		e 4
	2

181

it 2

Таким образом,

e 2 dt

O( 1 )..

Представим функцию f (x) в виде

f (x) f (0) f (x) f (0) f (0) xg(x), где функция g(x)

f (x) f (0)

непрерывно дифференцируема на отрезке 0; d . Таким образом

( )

f (0)e 4

O( 1 ) xg(x)e

dx.

(8.18)

Оценим оставшийся интеграл при

x 2

xg(x)e

g(x)d e

d 2

x 2

g(d )e

g(0) g (x)e

g(d )

g(0)

g (x)

Подстановка этой оценки в равенство (8.18) завершает доказательство леммы.

Теперь мы можем найти главный член асимптотики интеграла Фурье при наличии невырожденной стационарной точки.

Теорема 8.8. Пусть	f (x) и S(x)	бесконечно дифференцируемы на отрезке
a;b , функция S(x)	имеет единственную стационарную точку x0 a;b					и

S (x0 ) 0 . Тогда при
			i
b			i	2
F ( ) f (x)ei S ( x0 )dx		f (x0 )ei S ( x0 )e 4		2	O( 1 ) .


a				S (x0 )
Доказательство.
						то
Поскольку S (x) обращается в нуль лишь в точке					x0 и S (x0 ) 0 ,	то

при	a x x0 производная S (x0 ) 0 и функция S(x) монотонно убывает, а
при	x0 x b производная	S (x0 ) 0 и	S(x) монотонно возрастает.
Существует непрерывно-дифференцируемое			отображение : ; a;b ,

182

такое,

что

0 [ ; ], (0) x S и S( ( y)) S(x

) y2

. По

лемме

Морса

. Делая замену переменной в интеграле, получаем

(0)

S (x0 )

i y 2

F ( ) e

i S ( x0 )

f (

( y))

dy.

( y)e

Применим лемму Эрдейи

i y

f ( ( y) ( y)e

f (0) (0)e

)

(8.19)

f x

O( 1 ).

S (x0 )

Делая

замену

переменной

y u , для интеграла по

отрезку

;0 ,

получаем такую же оценку

f ( y)

i y 2

i u 2

( y)e

f ( u)

( u)e

O( 1 ).

(8.20)

S (x0 )

Сложение равенств (8.19) и (8.20) завершает доказательство теоремы.

Замечание. Если S (x0 ) 0 , то, используя сопряжение, получаем:

F ( ) f (x)ei S ( x) dx f (x)ei ( S ( x))dx

f (x

)e i S ( x0 ) e 4

O( 1 )

S (x0 )

f (x )ei S ( x0 )e

O( 1 ).

S (x0 )

Пример 8.6. Найдем асимптотику функции Бесселя

Jn (x)

ei( xsin n )d при x .

2 0

В этом примере

f ( ) e n ,

а фазовая функция S( ) sin имеет две

стационарные точки

. Соответственно,

асимптотика функции

Бесселя определяется суммой вкладов обеих стационарных точек. Поскольку S( 1) 1, S ( 1) 1, S( 2 ) 1, S ( 2 ) 1, то получаем

183

		2		n
J n	(x)		cos x
		x		2
					4

8.8. МЕТОД ПЕРЕВАЛА

Рассмотрим интеграл

O(x 1 ) при x .

F ( ) f (z)e	S ( z )	dz,	(8.21)

где – кусочно-гладкая кривая в комплексной плоскости С, а функции f (z) и S(z) являются аналитическими в некоторой области D, содержащей кривую . Будем рассматривать асимптотическое поведение функции F ( ) при x .

Идея метода основана на том, что согласно интегральной теореме Коши в односвязной области интеграл аналитической функции не зависит от выбора контура, соединяющего две фиксированные точки.

Предположим, что существует контур			такой, что
Предположим, что существует контур			такой, что
1. F ( ) f (z)e S ( z )dz f (z)e S ( z )dz;

2.Существует единственная точка z0 , в которой функция Re S(z) имеет строгий максимум и f (z0 ) 0;

3.ImS(z) const при z в окрестности точки z0 .

Пусть

–

малая

дуга контура

содержащая

точку

Тогда

существует

такое,

что

Re S(z) Re S(z )

при

z \ .

Пусть

z z(t) x(t) iy(t),

t0 t t1

–

регулярная

параметризация

контура такая, что z(0)

z , z : ; .

Используя принцип локализации, получим

F ( )

f (z)e

f z t

z t e

S ( z )

S z (t )

e S t dt 1 O( ) ,

e S Im S ( z0 ) f t

(8.22)

где f t f

z t z t , S t Re S z t .

184

Поскольку функция S t принимает только действительные значения, то асимптотику последнего интеграла можно найти с помощью метода Лапласа.

Контур, удовлетворяющий условиям 1, 2, 3, называют перевальным контуром.

Принципы нахождения перевального контура

Пусть S(z) U (z) iV (z)

z z(t) x(t) iy(t)

–

регулярная

параметризация

0 контура

такая, что

z(0) z0 . Поскольку t 0 –

z (t)

точка максимума функции Re S z t , то

Re S z t

U x xt U y

t 0

А так как Im S(z) const

на , то

Im S z t

Vx xt Vy yt 0 .

t 0

Таким образом, получаем систему уравнений

U y

Vx xt Vy yt 0

С учетом условий Коши-Римана U x Vy

,U y

Vx получаем

U x xt

U y

U x yt

U y xt

Так как определитель системы

x 2

y 2t

0 ,

то система

имеет единственное решение

z0 0.

Ux z0 U y z0

Vx z0

Таким образом, контур

обязательно должен проходит через точку

z0 , в которой S z0 0 .

Для изучения метода перевала нам понадобятся три леммы, которые мы приводим без доказательства.

Лемма 8.4 (Принцип максимума для гармонической функции.) Пусть функция U (z) является гармонической в ограниченной односвязной области

D и непрерывной в D . Если U (z) не является постоянной, то она не принимает своего максимального значения во внутренних точках области.

185

Лемма 8.5 Пусть	z0 – простая точка перевала функции S(z) , т.е.
S z0 0, S z0 0 .	Тогда в малой окрестности U точки z0 линия уровня

Re S(z) Re S(z0 ) состоит из двух гладких кривых, которые ортогональны в точке z0 и разбивают окрестность U на четыре сектора. Знаки функции

Re S(z) S(z0 )		в соседних секторах различны, и через секторы, в которых
Re S(z) Re S(z		) проходит гладкая кривая			, являющаяся перевальным
	0
контуром, т.е. Re S(z) Re S(z				) и ImS(z) ImS(z		0	) для всех z .
			0
Лемма 8.6	(О		линии наискорейшего		спуска). Пусть функция
W U (x; y) iV (x; y)			аналитическая в области				D C . Тогда линия

наискорейшего спуска функции U (x; y) задается уравнением V (x; y) const .

Нахождение главного члена асимптотики

Выведем формулу главного члена асимптотики интеграла (8.21) в

предположении существования перевального контура.

Теорема 8.8 Пусть функции

f (z) и S(z)

являются

аналитическими в

некоторой области D , содержащей кривую , z0

– простая точка перевала

S (z0 ) 0, S (z0 ) 0 , f z0 0

z z(t)

–

такая

параметризация

перевального контура, что z(0) z0 . Тогда

F ( ) f (z)e S ( z )dz f z0

e S z0

e 0 1 O( 2 ) ,

S (x0 )

где z(0) z0 0 arg z (0)

Доказательство.

Применяя к последнему интегралу в формуле (8.21) метод Лапласа, получим

t dt 1 O( )

F ( ) f (z)e S ( z )dz e S Im S ( z0 ) f t e S

S 0

f 0

i S ImS ( z0 )

1 O

S (0)

Поскольку на перевальном контуре ImS(z t ) const

и S (z0 ) 0 , то

S t

t 0

S z(t)

t 0 S (z0 ) z (0) 2.

Учитывая, что S 0 Re S(z0 ), f 0

f z0 z (0) , находим

186

F ( ) f (z)e S ( z ) dz


														1
f z0 e					2									1
					2
	S ( z0 )												2
													2
			z (0)						2	1	O
			z (0)						2	1	O
				S (0)			z (0)
												1
f z0		e S ( z0 )ei 0				2						1
						2
								1 O				2			.



						S (0)

Пример 8.10. Асимптотику функции Бесселя

	1	2
J n ( )		ei( sin n ) d при
	2
		0

мы уже находили при изучении метода стационарной фазы. Теперь найдем асимптотику методом перевала.

Стандартной заменой переменной z ei функция Бесселя приводится к виду

J ( )

e 2

2 i

zn 1

Найдем производные для функции S(z)

S(z)

, S (z)

z 2

Линия уровня

Re S(z) Re S(z

) x 2 1 1

2 0,

проходящая

через

точки перевала z1,2

i ,

состоит из

окружности

1 и прямой

x 0 .

Согласно лемме 2, перевальный контур должен быть касательным к биссектрисам соответствующих углов. Учитывая распределение знаков

функции Re S(z) ,		3				.
функции Re S(z) ,					2	.
	1		4		2	4
			4			4
							n
				2							1


Таким образом Jn ( )						cos				O	2
											2
									1			.
							2
							2	4

Замечание. Основные сложности при использовании метода перевала обычно бывают связаны с доказательством возможности деформации исходного контура в перевальный (с сохранением значения интеграла) и нахождением направления входа перевального контура в точку перевала. В примере, при нахождении асимптотики функции Бесселя, удается в явном виде найти линии уровня, проходящие через точки перевала, соответственно направления перевального контура в точках перевала легко находятся. В более общей ситуации для нахождения соответствующего угла могут быть использованы иные соображения.

187

9. ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

В настоящем разделе рассматривается метод конечных разностей, который является одним из наиболее распространенных численных методов решения уравнений с частными производными (уравнений математической физики).

9.1. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА

9.1.1. Понятие о методе конечных разностей. Основные определения и конечно-разностные схемы. Постановка начально-краевых задач

Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). В одномерном по пространству случае однородное (без источников энергии) уравнение теплопроводности имеет вид

u	a2		2u	, 0 x l, t 0.		(9.1)
t	a2		x2	, 0 x l, t 0.		(9.1)
t			x2
Если на границах		x 0		и x l	заданы значения искомой функции
u(x,t) в виде
u(0,t) 0 (x),				x 0,	t 0;	(9.2)
u(0,t) 1(x),				x l,	t 0,	(9.3)

т.е. граничные условия первого рода, и, кроме того, заданы начальные условия

u(x,t) (x), 0 x l, t 0,

(9.4)

то задачу (9.1)-(9.4) называют первой начально-краевой задачей для уравнения теплопроводности (9.1).

В терминах теории теплообмена u(x,t) – распределение температуры в пространственно-временной области T 0 x l; 0 t T , a2 – коэффициент температуропроводности, а (9.2), (9.3) с помощью функций

0 (x) , 1 (x) задают температуру на границах x 0 и			x l .
Если на границах x 0 и x l заданы		значения	производных искомой
функции по пространственной переменной
u(0,t) 0 (x),	x 0,	t 0;	(9.5)
x

188

u(l,t) (x),		x l,	t 0,	(9.6)
x	1
x

т.е. граничные условия второго рода, то задачу (9.1), (9.5), (9.6), (9.4) называют второй начально-краевой задачей для уравнения теплопроводности (9.1). В терминах теории теплообмена на границах в этом случае заданы тепловые потоки. Если на границах заданы линейные комбинации искомой функции и ее производной по пространственной переменной

u(0,t)

u(l, t)

u(0,t) 0 (x),

u(l, t) 1 (x),

x 0,	t 0;	(9.7)
x l,	t 0,	(9.8)

т.е. граничные условия третьего рода, то задачу (9.1), (9.7), (9.8), (9.4) называют третьей начально-краевой задачей для уравнения теплопроводности (9.1). В терминах теории теплообмена граничные условия (9.7), (9.8) задают теплообмен между газообразной или жидкой средой и границами расчетной области с неизвестными температурами u(0,t) , u(l, t) .

Для пространственных задач теплопроводности в области первая начально-краевая задача имеет вид

M (x, y, z) ,

t 0;

(9.9)

(M , t),

M (x, y, z) ,

t 0;

u(M , t)

(9.10)

u(M ,0) (M ),

M (x, y, z) ,

t 0.

(9.11)

Аналогично ставится вторая и третья начально-краевые задачи для пространственного уравнения задачи (9.9) – (9.11).

На практике часто ставятся начально-краевые задачи теплопроводности со смешанными краевыми условиями, когда на границах задаются граничные условия различных родов.

9.1.2. Понятие о методе конечных разностей. Применение метода конечных разностей к решению уравнений параболического типа

Основные определения, связанные с методом конечных разностей, рассмотрим на примере конечно-разностного решения первой начальнокраевой задачи для уравнения теплопроводности (9.1) – (9.4).

Нанесем на пространственно-временную область 0 x l , 0 t T конечно-разностную сетку h

189

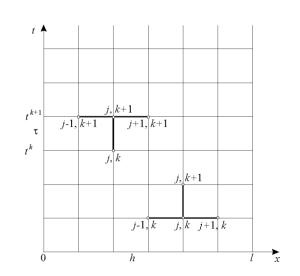
h x j jh, j		; tk k , k
	0, N		0, K		(9.12)

с пространственным шагом h l N и шагом по времени T K (рис. 9.1).

Рис. 9.1
Введем два временных слоя:		нижний	tk k ,		на котором
					(при k 0
распределение искомой функции u(x	j	,tk ), j 0, N	известно		(при k 0
	j
распределение определяется начальным		условием (9.4) u(x		,t0 ) (x		) ) и
			j		j

верхний временной слой tk 1 (k 1) , на котором распределение искомой


функции u(x			,tk 1 ), j	0, N	подлежит определению.
		j
	Сеточной функцией				задачи	(9.1) – (9.4)	(обозначение	u k	)	назовем
								j
однозначное отображение					целых	аргументов	j, k в значения			функции
uk u(x		,t k ) .
j	j
	На введенной сетке (9.12) введем сеточные функции u k ,							uk 1	, первая из
							j	j

которых известна, вторая – подлежит определению. Для ее определения в задаче (9.1) – (9.4) заменим (аппроксимируем) дифференциальные операторы отношением конечных разностей, получим

	u	k	ukj 1 ukj
	u	k	ukj 1 ukj
				O( ),		(9.13)
	t			O( ),		(9.13)
		j
		j
2u	k	uk	2uk uk
2u	k	uk	2uk uk
		j 1	j	j 1	O(h2 ).	(9.14)
x2			h2		O(h2 ).	(9.14)
x2	j		h2
	j

Подставляя (9.13), (9.14) в задачу (9.1) – (9.4), получим явную конечно-

разностную схему для этой задачи в форме

190

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2219 20 21 22 > Следующая >>>

Соседние файлы в папке 7 семестр

#
21.03.2016551.94 Кб40Б3.В6 Интеллектуальные технологии и представление знаний.pdf
#
21.03.2016541.87 Кб52Б3.ДВ6.1 Основы и системный анализ информационно управляющих процессов.pdf
#
21.03.2016618.63 Кб42Б3.ДВ7.1 Моделирование систем.pdf
#
21.03.2016573.24 Кб72Заочники.5 курс. Методическое пособие 2011г.Квалиметрия.docx
#
21.03.20163.79 Mб307Козлов, Кисоржевский_Теория информационных систем (2008).pdf
#
21.03.20163.81 Mб423Куликов К.Г., Фирсов А.Н. Уравнения и методы математической физики. 2011.pdf
#
21.03.2016440.86 Кб114Фирсов А.Н. (сост.) Уравнения математической физики (учебное пособие для заочников).pdf