Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Куликов К.Г., Фирсов А.Н. Уравнения и методы математической физики. 2011

.pdf

Скачиваний:

423

Добавлен:

21.03.2016

Размер:

3.81 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2213 14 15 16 17 18 19 20 21 22 > Следующая >>>

d			d	( 1)k z 2k 2v		( 1)k 2(k v)z 2k 2v 1
	z v Jv	(z)
dz				22k v k! (k v 1)
			dz k 0		k 0	22k v k! (k v 1)

	( 1)k z 2k v 1	(k v)
z v			z v
		v 1)
k 0 k !22k v 1 (k			k 0

Таким образом,

dzd z v Jv (z) z

	( 1)	k z	2k v 1


		2		z v J		(z).
	k ! (k v)			z v J	v 1	(z).
					v 1

v Jv 1 (z).						(6.26)

Аналогично получаем

	d	z v J		(z) z v J		(z).	(6.27)
			v		v 1
	dz

Продифференцировав в левых частях (6.26) и (6.27), получим

z v

(z) vz v J

(z) z v J

(z),

(6.28)

v 1

z v

(z) vz v 1J

(z) z v J

(z).

(6.29)

v 1

Откуда

(z)

(z) J

(z),

(6.30)

v 1

(z)

(z) J

(z),

(6.31)

v 1

Складывая и вычитая равенства (6.30) и (6.31), получим

(z) J

(z),

(6.32)

v 1

(z) J

(z).

(6.33)

v 1

Функции Бесселя

второго

третьего

рода удовлетворяют

тем же

рекуррентным соотношениям, что и функции первого рода, то есть соотношениям (6.26) – (6.33). При v, отличном от целого числа, справедливость этих формул для функций Бесселя второго рода (функций Вебера) вытекает из определения функции Вебера и соответствующих формул для функций первого рода. Для целого v требуемый результат следует из непрерывности рассматриваемых функций по отношению к индексу v, что позволяет осуществить в соотношениях (6.26) – (6.33) предельный переход при v n. Отметим еще формулы

121

z v J

(z) z v m J

(z),

v m

z dz

z v J

(z) ( 1)m z v m J

(z).

v m

z dz

Формулы (6.34) и (6.35) получаются путем повторного равенств (6.26) и (6.27). Приняв v 0 из (6.32), (6.33), получим

dzd J0 (z) J 1 (z);J 1 (z) J1 (z).

(6.34)

(6.35)

применения

6.7. ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ ДЛЯ ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ

Цилиндрические функции допускают простые интегральные представления, которые бывают двух типов: интегралы по некоторому отрезку (определенные интегралы) и контурные интегралы. Контурные интегралы удобнее, требуют меньше ограничений, но они более сложны. Определенные интегралы наиболее часто встречаются в приложениях, поэтому мы ограничимся рассмотрением формул этого типа. Одно из наиболее простых интегральных представлений для функций Бесселя принадлежит Пуассону. Будем исходить из формул (6.1) и (6.5)

			1														(x) ( y) .
B(x, y) t x 1 (1 t) y 1 dt,											B(x, y)						(x) ( y) .						Возьмем						в этих формулах
			0															(x y)
x k 1 2, y v 1 2 . Тогда
														1							1
	1				1		1			k					v
	1				1		1			k					v
	s			k		v								2							2								1
				k	2 (1 s)	v	2 ds															, k 0,1, 2,..., ;							Re(v)	.

													k v 1
	0												k v 1																2
Делаем замену s t 2 2tdt , тогда
																							1				1
								1								1					k			v
								1								1					k			v
							2 t		2k 1					2	v								2				2
											(1 t )				v	2 dt												.

																						k v 1
								0														k v 1
					1								2							1					v	1
Откуда					1								2							t 2k (1 t 2 )					v	2 dt.

		k v 1										1						1
								k					v						0
								k					v						0
												2						2

122

																		( 1)						k	z			2k v


																									2
Теперь можно записать Jv (z)																									2
Теперь можно записать Jv (z)																	(k 1) (k v 1)
															k 0		(k 1) (k v 1)
			( 1)k z				2k v					2					1												v		1									1
			( 1)k z				2k v					2								2k							2		v											1
																		t				(1 t						)			2 dt, Re(v)										.
																		t				(1 t						)			2 dt, Re(v)										.
	k 0		k!		2						1					1	0																							2
								k					v
								k					v
											2					2
			Меняем порядок суммирования и интегрирования, тогда
									z	v							1
																	1
								2				1														( 1)					k					2k
									2			1		(1 t 2 )v																	k		(zt )			2k
					Jv		(z)		2									2	dt														(zt )						.		(6.36)
					Jv		(z)				1							2	dt															1					.		(6.36)
											1											k		0										1			2k
									v				0												k! k										2		2k
									v				0												k! k										2
											2																							2
			Воспользуемся формулой (6.8), в которой примем z k 1 2 . Тогда
				1																										1
	2k			1																	2k									1								π 2k !.
2		k				k 1				π k 1 или										2			k									k!
2		k				k 1				π k 1 или										2			k									k!
				2																										2


		z	v
	2					1
	2					1
Тогда из (6.36) находим Jv (z)		2				(1 t	2	)
Тогда из (6.36) находим Jv (z)				1		(1 t		)
				1
	π v				0
	π v				0
				2

Окончательно получаем

v	1		( 1)	k	(zt )	2k

	2 dt						.
			2k !
		k 0

cos(zt )

						z		v			1				1
											1				1
					2
		(z)				2							(1 t 2 )v									π, Re(v)		1	.			(6.37)
																2
J																	cos(zt )dt,			arg z
J	v								1								cos(zt )dt,			arg z
	v																					2
																						2
					π v							0
					π v							0
									2
				Так как подынтегральная функция четная, то формулу (6.37) можно
переписать в виде
							z v
													1		1
													1		1
				(z)			2							(1 t 2 )v					cos(zt ) dt,		arg z		π, Re(v)			1	.	(6.38)
	J		v															2

												1
																							2
																							2
						π v							1
						π v							1
												2
				Применяя к формуле (6.38) подстановку t cos(θ),dt sin(θ) dθ , при
									1
которой					1 t 2 v							sin 2v (θ)			sin(θ) и θ π								при t 1; θ 0					при t 1,
которой					1 t 2 v					2		sin 2v (θ)			sin(θ) и θ π								при t 1; θ 0					при t 1,

получаем

123

				z	v
								π

				2								1
J	v	(z)							sin 2v (θ) cos(z cosθ) dt,	arg z	π, Re(v)		.	(6.39)

						1						2
						1						2
			π v				0
			π v				0
						2

Формула (6.38) или равносильная ей формула (6.39) – интегральное представление Пуассона.

Отметим еще основные интегральные представления для функций Ханкеля

vπi

izch(t ) vt

(6.40)

(1)

(z)

dt, Im z 0,

πi

vπi

e 2

H(2)

(z)

e izch(t ) vt dt,

Im z 0,

πi

v – любое.

6.8. ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ ИНТЕГРАЛЬНОГО ПРЕДСТАВЛЕНИЯ ПУАССОНА

Примем в (6.37) v 0, z x – вещественное число. Тогда

						2	1				1
							1	(1 t 2 )					cos(xt) dt, x .
		J (x)					0					2																			(6.41)
		J (x)				π						2																			(6.41)
		0				π
		0
Отсюда, в частности, следует																			2	1		dt			2						1.
															J			(x)									arcsint		1


																	0		π 0			(1 t 2 )			π				0
																			π 0			(1 t 2 )			π			1.
Таким образом,								для вещественных значений																x		J0 (x)		1.				Примем
теперь v n 1			2, n 0,1, 2,... Тогда
					z		v			1				1
										1				1
			2
		(z)			2						(1 t 2 )v						cos(zt )dt,				arg z		π, Re(v)							1		.
J																2

	v								1
	v																										2


				π v						0
				π v						0
									2

Отсюда следует, что функции Бесселя с положительным половинным индексом выражаются через элементарные функции. Но зная функции Бесселя с положительным половинным индексом, с помощью рекуррентных соотношений легко получить и функции с отрицательным половинным

			1
		z
		z			2
		2				1		2	1
			2						1

									2
индексом. Например, J 1	(z)						cos(zt )dt			sin( z).
индексом. Например, J 1	(z)						cos(zt )dt			sin( z).
				π		0		πz
2				π		0		πz

124

			1
		2
		2	2
Таким образом, J 1	(z)			sin( z).
Таким образом, J 1	(z)			sin( z).
		πz
2		πz
2

Лиувиллем доказано, что случай полуцелого индекса является единственным, когда цилиндрические функции приводятся к элементарным. В качестве еще одного примера применения интегрального представления для цилиндрических функций рассмотрим вычисление интеграла


I e ax J0 (bx)dx,	a 0,b 0.	(6.42)
0

Для этого воспользуемся формулой (6.41) и в интеграле сделаем замену

tsin . Будем иметь J0 (x) 2 π 2cos(x sin( ))d .

π0

Тогда интеграл (6.42) примет вид

π 2

I e ax dx

cos(bx sin( ))d

e ax cos(bx sin( ))dx.

Воспользуемся известной формулой e ax cos(bx)dx

, a 0,b 0.

2a π 2

Тогда I

a2 b2 sin 2 ( )

sin 2 ( )

(делаем замену ctg t )

d (at)

(at)

arctg

Итак, I e ax J

0 (bx)dx

6.9. АСИМПТОТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ ДЛЯ БОЛЬШИХ ЗНАЧЕНИЙ АРГУМЕНТА

Цилиндрические функции обладают простыми асимптотическими представлениями, удобными для аппроксимации этих функций при больших по модулю значениях z и фиксированном значении индекса v. Главные члены этих формул можно получить, исходя из дифференциальных уравнений, которым удовлетворяют рассматриваемые функции. Более точные

125

выражения можно получить, исходя из интегральных представлений. В данном параграфе мы не будем рассматривать строгий вывод асимптотических представлений (более подробно об асимптотических оценках см. главу «Асимптотические методы» настоящего пособия), а ограничимся следующими интуитивными соображениями.

Рассмотрим уравнение Бесселя (6.12)

u 0.

3ω

Сделаем подстановку u

z u

4 z5 .

Уравнение Бесселя примет вид

ω 0.

(6.43)

z 2

Если v ограничено, z , то вместо уравнения (6.43) можно рассматривать

ω 0.

Откуда ω Acos(z) Bsin( z) Ce

уравнение ω

Acos(z) Bsin( z)

Ceiz De iz

. Коэффициенты А, В, С, D зависят

от индекса v, а также от вида рассматриваемой цилиндрической функции.

Можно

получить

следующие

асимптотические

формулы:

H(1)v (z) πz2 e

	π										π
i( z (2v 1)		) O		1		, H(2)			2	e i( z (2v 1)		) O	1			,
	4							(z)			4

			z		3 2		v		πz					3

													z		2

при этом

arg z

π δ , v

ограничено.

Из определения

функций

Ханкеля следует Jv (z)

H(1)

(z) H(2) (z)

(z)

H(1)

(z) H(2)

(z)

Тогда

Jv (z)

cos z (2v

(6.44)

πz

3 2

Y (z)

sin

z (2v

(6.45)

πz

3 2

126

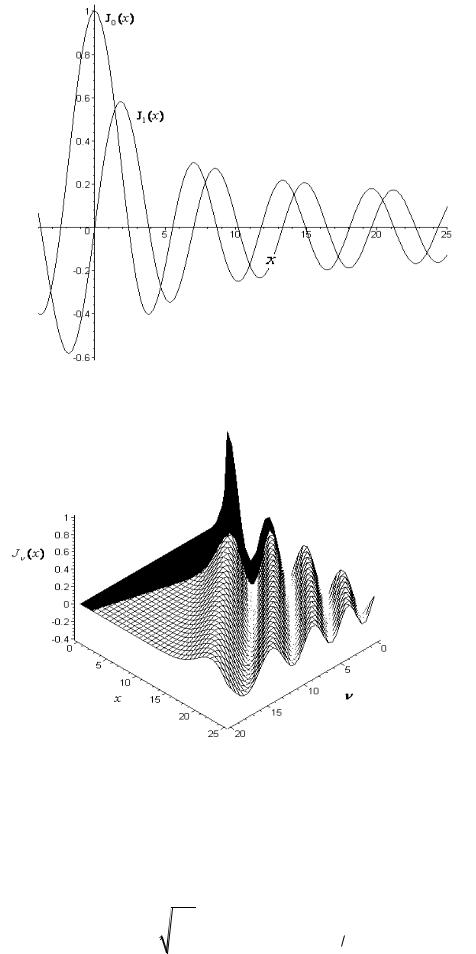
Рис. 6.3

Рис. 6.4

Таким образом, если функции Ханкеля на бесконечности имеют экспоненциальный характер, то функции Jv (z) и Yv (z) на бесконечности описываются формулами (6.44) и (6.45). В частности, для вещественных

z x и	v 0			2				1
		J0	(x)		cos x		O			.	Далее	J1 (x) J		(x) ,
									3 2
				z					3 2				0
				z		4	x
														127

следовательно, нули функции J1 (x) совпадают с экстремумами J0 (x) . Отсюда, в частности, вытекает, что уравнение J0 (x) бесчисленное множество корней. На рис. 6.3 представлены Бесселевых функций, полученные в Maple 10.

На рис.6.4 представлена поверхность	z f (x, ) J (x) ,
показывает, как изменяются функции J (x) ,	если непрерывно
переменные x, .

6.10. МОДИФИЦИРОВАННЫЕ ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ

Рассмотрим уравнение

	1		v	2
u		u 1			u 0, 0	x .
u		u 1			u 0, 0	x .
	x		x	2
	x		x

функции 0 имеет графики

которая

изменять

(6.46)

Сделаем замену переменной z ix ,

тогда

d 2u

i 2

, и

dx2

dz 2

уравнение (6.46) примет вид

d 2u

i2.

dx2

dz 2

Таким образом, мы пришли к уравнению Бесселя. Откуда

(1)

(6.47)

u AJv (z) BHv (z)

AJv xe

BHv

Таким образом, уравнение (6.46) интегрируется через цилиндрические функции мнимого аргумента. Однако пользоваться решением в форме (6.47) неудобно, так как при вещественном v функция (6.47) является комплексной. Вводятся в рассмотрение функции

πv

Iv (x) e

Jv xe

iπ

πv

(1)

(x)

(6.48)

(6.49)

которые называются модифицированными цилиндрическими функциями; функция (6.49) называется функцией Макдональда. Общее решение уравнения (6.46) теперь может быть записано в виде u(x) AIv (x) BKv (x).

Рассмотрим вкратце теорию этих функций. Из формул (6.17) и (6.48) следует

128

Iv (x)

k 0

x	2k v


2		; 0	x .	Таким образом,	Iv (x)	вещественно, когда
k! (k v 1)		; 0	x .	Таким образом,	Iv (x)	вещественно, когда
k! (k v 1)

x 0 , v вещественно. Получим вспомогательную формулу (будем пока считать, что v 0, 1, 2,...)

H(1)v

Следовательно,

Итак,

(z)

(z) iY (z) J

(z) i

Jv (z) cos(vπ) J v (z)

sin(vπ)

ivπ

2 Jv (z) e 2 J v (z)

sin(vπ)

ivπ

π I

(x)

ivπ

iπ

(ix) e 2

(ix)

(x) I

(z)

e 2

ie 2

sin(vπ)

2sin(vπ)

(z)

π I v (x) Iv (x)

(6.50)

2sin(vπ)

причем 0 x , v 0, 1, 2,...

Отсюда следует, что Kv (x) вещественно, если v вещественно. Покажем, что (6.50) приобретает неопределенный вид, если v стремится к целому числу. Действительно, имеем

		iπ
J	xe 2		( 1)n
	n

Jn xe

iπ		iπn		iπ		iπn		iπ
2	e	2		2		2		2
	e		J n xe		e		Jn xe		.


			I n ( x)				In ( x)

Таким образом, I n (x) In (x), n 0,1,2,..., и следовательно, формула (6.50) обращается в неопределенность при целом индексе v. Доопределим функцию Макдональда для целых индексов по формуле

Kn (x) lim Kv	(x)	( 1)n I

		2
v n

		Iv (x)
v (x)				, n 0, 1, 2, ... Из формулы
v		v

	v n		v n

(6.50) следует K v (x) Kv (x). Таким образом функция Макдональда есть четная функция индекса v. Для модифицированных цилиндрических функций существуют интегральные представления, аналогичные представлениям цилиндрических функций. Так, например, исходя из формулы (6.37)

129

Jv (z)

находим Iv (x)

						z		v
					2									1								1
					2									1								1
						2								(1 t			2			v						π, Re(v)	1
						2											2	)		v		2 cos(zt )dt,			arg z		1	,
										1								)				2 cos(zt )dt,			arg z		2	,
										1																	2
		π v										0
		π v										0
										2
			ivπ				x		v				ivπ
e	2					2			e 2						1								1
e	2					2			e 2						1								1
							2									(1 t			2			v
							2												2		)	v	2	cos(ixt)dt, или
											1										)		2	cos(ixt)dt, или
											1				0
				π v											0
				π v
											2

(x)

(1 t

)

2 ch(xt)dt.

π v

ivπ

Из формулы (6.40) H(1)

(z)

eizch(t ) vtdt,

Im z 0 находим

πi

iπv

πi

iπv

(x)

e 2

e xch(t ) vtdt

iπ

e xch(t ) vtdt

e xch(t )ch(t)dt, x 0,

так как e vt ch(vt) sh(vt) . Таким образом:

Kv (x)

e xch (t ) vt dt

e xch (t ) ch(vt)dt, x 0, v – любое.

Отметим

рекуррентные формулы,

которые легко получаются из формул

(6.32) и (6.33), 2

dIv (x)

Iv 1

(x) Iv 1

(x),

(x) Iv 1 (x) Iv 1 (x).

Аналогично 2

dKv

(x)

Kv 1 (x) Kv 1 (x),

Kv (x) Kv 1

(x) Kv 1

(x).

Отметим также асимптотические формулы

		x	v


Iv	(x)	2		,
Iv	(x)	(1 v)		,
		(1 v)

x 0; lim Kv (x) , поэтому функция Iv (x) ограничена при

x 0

v 0; I	(x)	ex	, K		(x)	π	e x , x .
v 0; I	(x)		, K	v	(x)		e x , x .
v		2πx		v		2x
		2πx				2x

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2213 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в папке 7 семестр

#
21.03.2016551.94 Кб40Б3.В6 Интеллектуальные технологии и представление знаний.pdf
#
21.03.2016541.87 Кб52Б3.ДВ6.1 Основы и системный анализ информационно управляющих процессов.pdf
#
21.03.2016618.63 Кб42Б3.ДВ7.1 Моделирование систем.pdf
#
21.03.2016573.24 Кб72Заочники.5 курс. Методическое пособие 2011г.Квалиметрия.docx
#
21.03.20163.79 Mб307Козлов, Кисоржевский_Теория информационных систем (2008).pdf
#
21.03.20163.81 Mб423Куликов К.Г., Фирсов А.Н. Уравнения и методы математической физики. 2011.pdf
#
21.03.2016440.86 Кб114Фирсов А.Н. (сост.) Уравнения математической физики (учебное пособие для заочников).pdf