Пример 2 (распределение Пуассона). Для распределения Пуассона (7.12), как мы знаем, Mξ = λ. Поэтому:

Таким образом, для распределения Пуассона Dξ = λ (т.е. дисперсия по величине совпадает с математическим ожиданием).

Среднеквадратическоеотклонениебудет,следовательно,равно σ = λ .

7.4. Независимые случайные величины

Мы уже видели, какое большое значение имеет понятие независимости для случайных событий. Оказывается, что аналогичное понятие можно естественным образом ввести и для случайных величин.

Пусть в результате опыта могут наблюдаться две случайные величины ξ и η. Слова «могут наблюдаться» мы понимаем в том смысле, что для любых двух числовых множеств А и В мы можем сказать, произошло или не произошло каждое из двух событий {ξ A}и {η B} (напомним, что так для краткости обозначаются множества {ω:ξ(ω) A} и {ω:η(ω) B} ).. «Независимость» случайных величин интуитивно понимается так, что, зная результат наблюдения над одной случайной величиной, мы ничего не можем сказать дополнительно о другой случайной величине. Этим мотивируется следующее

Определение 7.5. Две случайных величины ξ и η называются

125

независимыми, если для любых двух числовых множеств А и В события {ξ A} и {η B} независимы, т.е. (см. § 2, п. 2.2) вероятность их произведения равна произведению вероятностей этих событий:

(7.15)

Замечание. Произведение событий {ξ A} и {η B}, т.е. совокупность всех тех ω Ω, для которых одновременно ξ(ω) A и η(ω) B :

{ξ A} {η B}={ω:ξ(ω) A,η(ω) B}

мы далее для краткости будем обозначать символом {ξ A,η B} .

Аналогично,символом {ξ = ai ,η=bj} будетобозначенасовокупностьвсехтех

ω Ω , для которых одновременно ξ(ω) = ai и η(ω) =bj , т.е. произведение событий {ξ = ai}={ω:ξ(ω) = ai}и {η=bj}={ω:η(ω) =bj}:

опр

{ξ = ai ,η=bj} = {ξ = ai} {η=bj}={ω:ξ(ω) = ai ,η(ω) =bj}.

Пусть x1, x2 , ..., xn , ... – возможные значения д.с.в. ξ и P(ξ = xi ) = pi , y1, y2 , ..., ym , ...– возможные значения д.с.в. η и P(η= yj ) = qj .

Если случайные величины ξ и η – независимы, то полагая в (7.14) A ={xi} и B ={yj} (одноточечные числовые множества), получим:

всех y1, y2 , ..., ym , ... выполнено равенство (7.16), то случайные величины ξ иη– независимы.Действительно,длялюбыхчисловыхмножеств АиВимеем:

что и требовалось.

Мы видим, таким образом, что справедлива следующая теорема.

126

Теорема 7.4. Длянезависимости случайныхвеличинξиη необходимои достаточно, чтобы для любых xi и yj было выполнено равенство (7.16).

Установим теперь некоторые свойства математического ожидания и дисперсии, связанные с понятием независимости случайных величин.

Теорема 7.5. Если случайные величины ξ и η независимы и существуют

Обратимся теперь к дисперсии и рассмотрим вопрос о дисперсии суммы ξ + η двух случайных величин не предполагая, поначалу, что эти величины независимы. Вычислим:

D(ξ+η) = M[ξ+η−M(ξ+η)]2 (7=.6) M[(ξ −Mξ)+ (η−Mη)]2 =

= M(ξ −Mξ)2 + M(η−Mη)2 + 2M[(ξ −Mξ)(η−Mη)].

Выражение cov(ξ,η)=M[(ξ −Mξ)(η−Mη)] называется ковариацией величин ξ и η. Для независимых случайных величин в силу (7.8) и (7.17):

cov(ξ,η) = M(ξ −Mξ)M(η−Mη) = 0.

Таким образом, нами доказана Теорема 7.6. Для любых случайных величин

127

получится по индукции.

Итак, пусть случайные величины ξ,η,ς попарно независимы. Тогда:

D(ξ+η+ς) = D(ξ+(η+ς)) = Dξ + D(η+ς)+2cov(ξ,η+ς) =

Для cov(ξ,η+ς) имеем:

cov(ξ,η+ς) = M[(ξ −Mξ)(η+ς−M(η+ς))]= = M[(ξ −Mξ)(η+ς−Mη−Mς)].

Производя перемножение внутри квадратных скобок и используя свойства математического ожидания и попарную независимость случайных величин ξ,η,ς, получаем cov(ξ,η+ς) = 0. Тогда формула (7.21) дает:

D(ξ+η+ς) = Dξ + Dη+ Dς

Теорема доказана.

7.5. Неравенство Чебышёва

В этом разделе мы познакомимся с некоторыми важными результатами, использующими понятия математического ожидания, дисперсии и независимости случайных величин.

128

Теорема 7.7 (неравенство Чебышёва).

Пусть имеется д.с.в. ξ, у которой существуют Mξ и Dξ. Тогда для любого ε > 0 справедливо неравенство:

Замечания.

1. Обозначение P(ξ −Mξ ≥ ε) есть сокращенное обозначение для вероятности

P{ω: ξ(ω)−Mξ ≥ ε}= ∑ P(ξ = xi )

xi: xi −Mξ ≥ε

( x1, x2 , ..., xn , ...– возможные значения случайной величины ξ).

2. Смысл неравенства Чебышёва56 состоит в том, при малых значениях дисперсии Dξ большие отклонения случайной величины ξ от ее математического ожидания Mξ маловероятны. Это подтверждает представление о дисперсии как мере отклонения случайной величины от ее математического ожидания.

Доказательство теоремы. Имеем:

Dξ = ∑(xi −Mξ)2 P(ξ = xi ).

xi

Если суммированиепо всем xi заменить суммированиемтолькопотем xi ,для которых xi −Mξ ≥ ε, то сумма не увеличится. Поэтому:

Dξ ≥ ∑ (xi −Mξ)2 P(ξ = xi )≥

xi: xi −Mξ ≥ε

≥ ε2 ∑ P(ξ = xi ) = ε2P(ξ −Mξ ≥ ε),

xi: xi −Mξ ≥ε

что, очевидно, эквивалентно (7.22).

7.6. Закон больших чисел

56 Пафнутий Львович Чебышёв (1821-1894) – один из наиболее видных российских математиков второй половины XIX века, создатель петербургской научной школы, академик Петербургской Императорской Академии Наук с 1856 года.

129

Случайные величины возникают в приложениях как результаты измерений, причем либо сами измерения подвержены случайным ошибкам, либо объекты измерения случайным образом выбираются из некоторой совокупности. Давно было замечено, что, в то время как результаты отдельных измерений ξ1,ξ2 ,...,ξn могут колебаться сильно, их средние

арифметические 1n (ξ1 +ξ2 +...+ξn ) обнаруживают (при больших n) гораздо

бóльшую устойчивость, т.е. меняются незначительно (так называемая «устойчивость средних»). Как правило, указанная величина среднего арифметического совокупности n измерений одной и той же физической величины принимается за ее среднее значение, т.е. приближенное значение, которое можно использовать в тех вычислениях, где эта физическая величина встречается. Здесь, однако, имеется определенная тонкость, требующая разъяснения.

Дело в следующем. При измерении физической величины мы не можем заранее указать все факторы, которые в той или иной степени повлияют на показания приборов, с помощью которых мы это измерение производим. Поэтому, результат каждого такого конкретного измерения представляет собой одно из возможных значений некоторой случайной величины, которая определяется совокупностью факторов (явлений-причин), которые сопровождают данный эксперимент по измерению интересующей нас физической величины. При проведении следующего (независящего от предыдущего) измерения той же самой физической величины, даже при соблюдении одинаковости57 условий, в которых измерения проводятся, мы уже будем иметь дело с другой случайной величиной, одно из возможных значений которой и будет наблюдаться при втором измерении.

Иными словами, каждый конкретный эксперимент по измерению данной физической величины порождает свою случайную величину, одно из

57 В той мере, в которой такую «одинаковость» можно обеспечить. 130

возможных значений которой и наблюдается экспериментатором как показание соответствующего измерительного прибора. Таким образом, мы имеем дело с несколькими (по числу измерений) независимыми случайными величинами. Каждая такая случайная величина имеет свои собственные числовые характеристики (математическое ожидание и дисперсию), которые определяются распределениями каждой из этих случайных величин в отдельности. Интуитивно ясно, что разумнее всего в качестве значения измеряемой в эксперименте физической величины принять ее математическое ожидание, т.е. величину Mξ = ∑xj pj .

Однако мы никогда непосредственно этого математического ожидания вычислить не можем, так как нам неизвестно распределение соответствующей случайной величины. На практике в качестве значения измеряемой физической величины принимают арифметическое среднее различных измерений этой величины, т.е. значение (x(1) + x(2) +... + x(n) )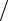n , где в числителе стоят не возможные значения одной случайной величины, а какие-то из возможных значений разных независимых случайных величин (представляющих различные измерения). Естественно возникает вопрос, в какоймеретакойподходявляетсяудовлетворительным,т.е.великалиразница между математическим ожиданием Mξ и упомянутым арифметическим средним различных измерений?

Следующая теорема, представляющая собой знаменитый закон больших чисел (в форме Чебышёва), дает ответ на поставленный вопрос.

Теорема 7.8. Пусть случайные величины ξ1,ξ2 ,...,ξn попарно независимы и их дисперсии ограничены в совокупности, т.е. Dξi ≤ c для всех

Доказательство. По формуле (7.6):

Далее, в силу попарной независимости ξ1,ξ2 ,...,ξn , по формуле

(7.20), с учетом равенства D(Cξ) =C2Dξ,58 получаем:

где последнее неравенство следует из условия теоремы. По неравенству Чебышёва получаем окончательно:

Теорема доказана.

Следствие. Если Mξ1 = Mξ2 =...= Mξn = a , то для любого ε > 0 при

n →∞

Доказательство очевидно.

Это следствие и является выражением «устойчивости средних», о котором говорилось в начале этого пункта. Действительно, при измерении одной и той же физической величины естественно предполагать, что случайныевеличины,характеризующиекаждоеконкретноеизмерение,имеют одинаковые распределения и, следовательно, одинаковые математические ожидания. Таким образом, при «достаточно большом количестве измерений»,

58 См. замечание к формуле (7.14).

132

замена математического ожидания арифметическим средним измеренных значений физической величины вполне оправдано.

Соотношение (7.23) является крайне важным, но обладает тем же недостатком, что и теорема Пуассона: она не дает возможности достаточно ясно интерпретировать термин «достаточно большое количество измерений». Для испытаний Бернулли соответствующее уточнение дает теорема Муавра-Лапласа.Вслучаежезаконабольшихчиселтакуюрольиграетоднаиз важнейших теорем теории вероятностей – центральная предельная теорема. Доказательство этой теоремы достаточно сложно, чтобы его можно было изложить в этом пособии; мы приведем только ее «облегченную» формулировку для частного случая, относящегося к формуле (7.23).

Теорема 7.9. Пусть случайные величины ξ1,ξ2 ,...,ξn попарно независимы и имеют одинаковые математические ожидания и дисперсии:

где Φ(x) – нормальная функция распределения (§ 6д, п. 6д.2). Напомним, что эта же функция Φ(x) встречается в формулировке

теоремы Муавра-Лапласа (теорема 6д.1).

Формула (7.24) позволяет связать число необходимых наблюдений (измерений) с требуемой точностью оценки математического ожидания a измеряемой величины. Так, при εn =3σ («правило 3σ») получаем

что вполне достаточно для практических целей. Заметим, что ε убывает, как величина 1n . Отсюда видно, что ошибка от замены математического

пропорциональна квадратному корню из числа наблюдений. Это говорит о том, что иногда бывает лучше сделать более точный прибор (что позволяет уменьшить дисперсию σ2 ), чем надеяться увеличить точность за счет увеличения числа наблюдений. Вообще, статистикой надо пользоваться тогда, когда исчерпаны технические возможности.

134

Фирсов Андрей Николаевич

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Учебное пособие

Налоговая льгота – Общероссийский классификатор продукции ОК 005-93, т. 2; 95 3005 – учебная литература

Подписано в печать 28.04.2014. Формат 60x84/16. Печать цифровая. Усл. печ. л. 7,0. Тираж 52. Заказ 11827b.

Отпечатано с готового оригинал-макета, предоставленного автором, в типографии Издательства Политехнического университета.

195251, Санкт-Петербург, Политехническая ул., 29.

Тел.: (812) 552-77-17; (812) 550-40-14

135