
Учебные материалы ИКНТ 1-8 семестры / 3 семестр / Выч.мат / лекции
.pdf
A1=V1A=V1(a1 a1 … a1)=(V1a1 V1a2 … V1an).
В соответствии с теоремой всегда можно построить V1 таким образом, чтобы V1a1 имел нули ниже главной диагонали.
Далее подбираем V2 так, чтобы во втором столбце V2A1 обнулить элементы ниже главной диагонали. В этих условиях будут сохранены нули ниже главной диагонали и в первом столбце. Проделав эти операции (n-1)
раз, получим Vn-1Vn-2…V1A=R . Vn-1Vn-2…V1=QT ортогональная матрица.
QTA=R или A=QR.
Правило выбора вектора wk. (Vk=E-2wk wTk).
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
w |
|
|
|
0,0,...0, a |
s , a |
, a |
,..., a |
|
; |
|||||
k |
|
k |
|
|
kk |
|
k k 1,k |
k 2,k |
n,k |
|
||||
|
|
|
|
k 1нулей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
1 |
|
|
|
|
|
|
|||
sk |
|
|
aik2 ; k |
|
|
|
; k=1, n 1. |
|||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|||||||||||
|
|
|
i k |
|
|
2sk (sk akk ) |
|
|
|
|||||
Знак sk совпадает со знаком –akk.
Количество требуемых операций Q≈ 4/3)n3. Метод обладает повышенной вычислительной устойчивостью в сравнении с методом Гаусса.
Упражнения. Разработать программу на языке Matlab,
реализующую QR разложение с использованием метода отражения.
Применить программу для решения заданной системы линейных алгебраических уравнений.
11.5.Сравнительный анализ вычислительной устойчивости прямых методов решения систем линейных
алгебраических уравнений.
141

Метод |
Число |
Точность |
Доп. |
Примечания |
|
операций |
(f(n)) |
память |
|
|
|
|
|
|
Метод |
2/3n3 |
αn2 |
0 |
α<∞(ед. |
Гаусса |
|
|
|
деление) |
|
|
|
|
α<2n-1(част. |
|
|
|
|
выбор). |
|
|
|
|
реально |
|
|
|
|
α< ÷ n |
|
|
|
|
|
Метод |
1/3n3 |
1 |
0 |
|
Холецкого |
|
|
|
|
|
|
|
|
|
Метод |
2n3 |
2.9n |
0 |
|
вращения |
|
|
|
|
|
|
|
|
|
Метод |
4/3n3 |
2.9n |
2n |
|
отражения |
|
|
|
|
|
|
|
|
|
Вычислительная погрешность оценивается по формуле
||x * x || (2condA) f (n) M .
||x ||
11.6.Итерационные методы решения систем линейных алгебраических уравнений.
Итерационный метод задает процедуру построения последовательности векторов x1, x2, …, xn, … такую, что xn→x* при n→∞,
где x* точное решение исходной системы Ax=b. Построение последовательности прерывается при достижении заданной погрешности ε
||xn-x*||<ε.
Указанная процедура может быть сформирована следующим образом. Эквивалентным преобразованием исходная система приводится к виду x=Cx+d , (1)
после чего заменяется разностной системой
142

xn+1=Cxn+d (2).
Требуют ответа следующие вопросы.
1.Как осуществить переход к системе (1).
2.Сходится ли итерационный процесс, а если сходится, то к какому пределу.
3.Какова скорость сходимости.
Иначе xn-x*=C(xn-1-x*)+C(xn-x*). Тогда
|| xn-x*||=||C(xn-1-x*)+C(xn-x*)|| ||C|| ||(xn-1-x*)||+||C|| ||(xn-x*)|.
Таким образом, |
|| x x*|| |
|| C || |
|| x |
x |
|| . |
|
|||||
|
n |
1 || C || |
n |
n 1 |
|
|
|
|
|
|
При переходе от исходной системы к системе (1) требуется сформировать матрицу С с указанными свойствами. Универсальный способ такого перехода отсутствует. В каждом конкретном случае требуется анализировать индивидуальные особенности исходной системы.
Рассмотрим некоторые из широко используемых приемов формирования системы (1).
Метод Якоби.
Пусть диагональные элементы матрицы А отличны от нуля. Тогда исходную систему можно представить в виде
|
k 1 |
a |
|
|
|
m |
|
a |
|
|
|
b(k ) |
|
|||
x(k ) |
kj |
x( j ) |
|
kj |
x( j ) |
|
|
, k 1,2,..., m. |
||||||||
a |
a |
a |
||||||||||||||
|
j 1 |
kk |
|
|
j k 1 |
kk |
|
|
|
kk |
|
|||||
Здесь А Rm×m, x(k) – k-ый компонент вектора x. |
||||||||||||||||
Переходя к разностной системе, получаем |
|
|||||||||||||||
(k ) |
k 1 |
akj |
|
( j ) |
|
m |
|
akj |
( j ) |
|
b(k ) |
|
||||
xn 1 |
|
|
|
xn |
|
|
|
|
|
xn |
|
|
|
|
, k 1,2,..., m. (4) |
|
a |
a |
|
a |
|||||||||||||
|
j 1 |
|
|
|
j k 1 |
|
|
|
|
|||||||
|
|
kk |
|
|
|
|
kk |
|
|
|
kk |
|
||||
Это метод Якоби. В матричной форме получаем xn+1=-D-1(A-D)xn+D-1b
или D(xn+1-xn)+Axn=b.
Здесь D диагональная матрица с диагональными элементами матрицы А, C=-D-1(A-D). Чем больше абсолютные величины диагональных элементов матрицы А по сравнению с модулями остальных ее элементов,
тем меньше модули элементов матрицы С и ее норма и тем выше скорость сходимости итерационного процесса.
Метод Зейделя.
К моменту вычисления xn+1(k) значения xn+1(j) для j<k уже определены.
Поэтому формулу (4) можно переписать в виде
144
(k ) |
k 1 |
akj |
( j ) |
m |
akj |
( j ) |
|
b(k ) |
|
xn 1 |
|
|
xn 1 |
|
|
xn |
|
|
, k 1,2,..., m. |
a |
a |
|
|||||||
|
j 1 |
|
j k 1 |
|
|
a |
|||
|
kk |
|
kk |
|
|
kk |
|||
Это метод Зейделя.
Введем диагональную матрицу D, а также нижнюю и верхнюю треугольные матрицы А1 и А2 с нулевыми главными диагоналями.
Элементы этих матриц совпадают с соответствующими элементами матрицы А, т. е. A=D+A1+A2. матричная форма метода Зейделя имеет вид
xn+1=-D-1 A1xn+1 - D-1 A2 xn +D-1b
или (D+A1)(xn+1-xn)+Axn=b.
Для метода Зейделя C=(D+A1
О сходимости методов Якоби и Гаусса – Зейделя.
Теорема1. Предположим, что матрица A строго диагонально
n
доминирующая, т. е.| aii | | aij |, i=1, n.
j 1
Тогда итерации Якоби и Гаусса – Зейделя сходятся к единственному решению уравнения Ax=b при любом начальном приближении x(0).
Теорема 2. Если A симметрическая и положительно определенная матрица, то при любом начальном приближении x(0) итерации Гаусса – Зейделя сходятся к единственному решению уравнения Ax=b
Обычно скорость сходимости выше у метода Зейделя. Однако встречаются системы, для которых нарушается сходимость метода Зейделя , а метод Якоби функционирует нормально. Бывает и наоборот.
Обобщение матричных форм методов Якоби и Зейделя приводит к канонической форме одношагового итерационного метода
B |
xn 1 xn |
Ax b. |
|
||
n 1 |
|
n |
|
n 1 |
|
Известны многочисленные модификации итерационных методов.
Например, в качестве вариантов канонической формы можно перечислить 1. Метод простой итерации: Bn+1=E, τn+1=τ.
145
2.Итерационный метод Ричардсона: Bn+1=E, τn+1 переменный параметр.
3.Метод Якоби: Bn+1=D, τn+1=1.
4.Метод верхней релаксации: Bn+1=D+ωA1, τn+1=ω, 0<ω<2. Для ω=1 получаем метод Зейделя.
Итерационные методы используются для решения систем с большими разреженными матрицами. В этих условиях критичной становится скорость сходимости. Существенно повысить скорость сходимости можно, подбирая оптимальные значения τn+1 и Bn+1.
11.7.Решение линейных алгебраических систем с трехдиагональной матрицей методом прогонки.
Требуется решать линейную систему |
|
|
|
||||
Ax = r , |
(1) |
|
|
|
|
|
|
где x=(x0, x1, ….,xN)T, r = (r0, r1, ….,rN)T, |
|
|
|
||||
|
c0 |
d0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1 |
c1 |
d1 |
|
|
|
|
|
|
b2 |
c2 |
d2 |
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bN 1 |
cN 1 |
dN 1 |
|
|
|
|
|
|
|||
|
|
|
|
|
bN |
cN |
|
|
|
|
|
|
|
||
Нулевое соотношение системы (1) с0x0 + d0x1 = r0 решаем относительно x0:
x |
d0 |
x |
r0 |
или x |
|
|
|
x |
, где |
|
|
d0 |
, |
|
r0 |
. |
|
|
0 |
0 |
0 |
|
|
||||||||||
0 |
c0 |
1 |
c0 |
|
|
1 |
0 |
|
c0 |
0 |
|
c0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следующее уравнение b1x0 + с1x1 + d1x2 = r1 , используя выражение для x0, преобразуем следующим образом: b1 δ0 x1 +b1λ0 + с1x1 + d1x2 = r1 или
(b1 δ0 + с1 )x1 = - d1x2 +( r1 -b1λ0), получим x1 = δ1 x2 +λ1, где
146

|
|
|
d1 |
, |
r1 b1 0 |
. |
|
1 |
|
|
|||||
|
|
b1 0 c1 |
1 |
b1 0 |
c1 |
||
|
|
|
|
||||
Рассмотрим k – ое соотношение bkxk-1 + сkxk + dkxk+1 = rk , предполагая, что на предыдущем k-1 – ом шаге было получено
xk-1 = δk-1 xk +λk-1 . Получим bk δk-1 xk +bkλk-1 + сkxk + dkxk+1 = rk , или
|
|
|
|
xk = δk xk+1 +λk , |
(2) |
|||
где |
|
|
|
|
|
|
||
|
|
|
dk |
|
, |
|
rk bk k 1 |
. (3) |
k |
|
|
|
|||||
|
|
bk k 1 |
|
k |
|
bk k 1 ck |
|
|
|
|
|
ck |
|
|
|||
Из соотношений (3) можно найти все коэффициенты δk , λk для
k 1, N 1, преобразуя систему (1) к соотношениям вида (2). Из последнего уравнения (1) bNxN-1 + cNxN = rN после подстановки xN-1 = δN-1 xN +λN-1 получим
x |
|
|
rN bN N 1 |
. |
|
N |
|
||||
|
|
bN N 1 |
cN |
||
|
|
|
|||
Затем по соотношению (2) в обратном порядке находят остальные неизвестные xN-1, xN-2, …, x1, x0 .
Процесс вычисления коэффициентов δk , λk для k 1, N 1, по соотношениям (3) называется прямым ходом прогонки, а нахождение неизвестных по формуле (2) – обратным ходом прогонки.
Если выполняется условие |ck|≥|bk| + |dk|, то говорят, что матрица А является матрицей с доминирующей главной диагональю. Указанное условие гарантирует корректность и вычислительную устойчивость алгоритма. При этом знаменатель δk в (3)не равен нулю, что обеспечивает выполнение прямого хода. Дополнительное условие |ck|≥|bk| обеспечивает
δk 1, что делает вычислительно устойчивым обратный ход.
Являясь модификацией метода Гаусса, метод прогонки существенно более экономен и требует для своей реализации всего 8(N+1) операций.
147
12.Методы отыскания решений нелинейных уравнений.
12.1. Постановка задачи.
Требуется вычислить корни системы из n уравнений с n
неизвестными
f1 (x1, x2 ,..., xn ) 0 f2 (x1, x2 ,..., xn ) 0
...............................
fn (x1, x2 ,..., xn ) 0
Матричная запись F(x)=0, x=(x1, x2,…,xn)T, F=(f1, f2,…,fn)T.
Ограничимся отысканием вещественных корней.
На первом этапе займемся отысканием решения одного нелинейного уравнения. Ограничимся вещественными корнями.
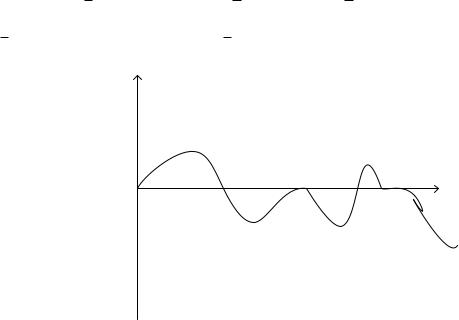
Корень x простой, если f'( x )≠0, корень x имеет кратность m, если f(k)( x ) = 0, k=1, 2, …, m-1 и f(m)( x )≠0.
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
|
|
x1, x2, x4 – простые корни; x3 – корень четной степени; x5 кратный корень нечетной степени
12.2. Основные этапы решения.
Локализация корня.
148

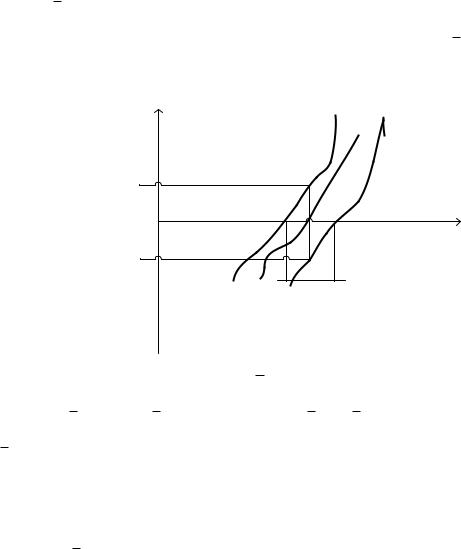
Корень локализован на отрезке [a,b], если f(a)f(b)<0 и f'(x)
знакопостоянна на этом отрезке. К сожалению, кратный корень не может быть локализован таким образом. Можно использовать построение графиков и таблиц. Особенно трудна задача локализации при решении систем уравнений. Часто в этом случае приходится использовать метод проб и ошибок.
Итерационное уточнение корня.
Используются итерационные численные методы. Задается закон формирования числовой последовательности xn+1=g(xn, xn-1,…) такой, что xn→ x при n→∞. Выполнение последнего условия означает сходимость метода, что является необходимым условием его работоспособности.
Метод называется одношаговым, если список аргументов функции g
содержит только один предшествующий член последовательности. Если в этом списке присутствуют несколько предыдущих членов, метод называется многошаговым.
Если существует такая ϭ окрестность корня, что когда x ϭ,
выполняется условие
|xn+1- x | C|xn- x |p, C>0 , p≥1,
говорят о p-ом порядке скорости сходимости метода. Линейной скорости соответствует p=1. Если при этом C=q<1, метод сходится со скоростью геометрической прогрессии. Метод обладает сверхлинейной сходимостью при p>1. В этом случае скорость сходимости возрастает по мере уменьшения погрешности |xn- x |.
Сказанное справедливо для системы, если использовать нормы векторов вместо абсолютного значения.
12.3. Обусловленность задачи вычисления корня.
Пусть функция f(x) в окрестности корня вычисляется с погрешностью |f(x)-f*(x)| (f).Здесь f*(x) возмущенная функция. Тогда за
149
решение x можно принять любое значение x*, которое является точным решением любой функции f*(x), обладающей свойством |f( x )-f*(x)| (f)
или |f*(x)| (f) .
2 (f)
f(x) 2ρ
Разлагаем f(x) в окрестности x в ряд Тэйлора
f(x)-f( x )=f'(ξ)(x- x ), т. е. f(x)=f'(ξ)(x- x ), x- x =f(x)/f'(ξ),
|(x- x )| f(x)| / |f'(ξ)|. Значение функции f(x) уменьшается при приближении x к корню. Когда оказывается |f(x)| (f) , дальнейшее уточнение корня
становится невозможным. Таким образом, радиус неопределенности корня
ρ (f) / |f'( x )| .
Практические выводы.
1. Непосредственный расчет ρ по последней формуле невозможен.
Однако так как при попадании в область неопределенности погрешность очередных уточнений перестает уменьшаться, можно воспользоваться
правилом Гарвика qn |
|
| xn |
xn 1 |
| |
1. При выполнении этого условия |
|
| xn 1 |
xn 2 | |
|||||
|
|
|
||||
расчет нужно прекратить. Это правило легко распространяется на систему при замене абсолютных значений на нормы.
2. Точность вычисления корня заведомо не может быть выше εмаш.
150
