5.1.3. Уравнение движения одноемкостного объекта.

В

качестве примера рассмотрим объект, показанный на рис. 21. Управляемым параметром является уровень жидкостиh, управляющим воздействием поворот входного вентиля x, параметром нагрузки - положение выходного вентиля L. Аккумулирующая способность этого объекта характеризуется площадью поверхности жидкости F. При отклонении управляемого параметра от равновесного значения h_р (рис.21) нарушается условие установившегося режима Q_п = Q_о = Q_р . Согласно уравнению сплошности жидкости, скорость изменения объема равна разности расходов подведенной и отведенной жидкости

(5.1)

Учитывая, что Q_п и Q_о являются функциями управляемого параметра h и, кроме того, зависят соответственно от управляющего воздействия x и параметра нагрузки L, можно определить параметры подвода и отвода. Для этого функции Q_п (h, x) и Q_о (h,L) раскладываются в ряд, причем предполагается, что вблизи точки равновесия производными второго и высших порядков можно пренебречь. Тогда

(5.2)

При подстановке соответствующих величин из (5.2) в (5.1) получаем

(5.3)

Для того, чтобы перейти к безразмерным параметрам, делим и умножаем каждое слагаемое на номинальные значения h_н, x_н, L_н, а также делим обе части уравнения на номинальный расход Q_н (5.4).

(5.4)

Вводим обозначения: (h - h_p)/h_н = φ - управляемый параметр,

(х - х_р)/х_н = ξ - управляющее воздействие,

(L - L_р)/L_н = λ - параметр нагрузки;

Обозначим также F(h_н/Q_н) = Т_а - время объекта,

- коэффициент самовыравнивания

И

примем

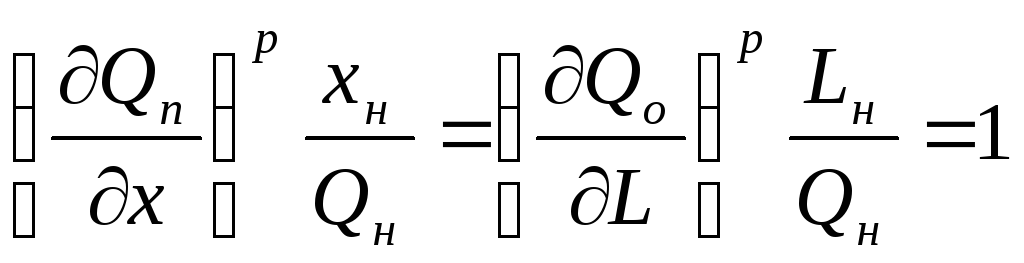
Последнее равенство обеспечивается за счет подбора номинальных значений параметров x, L, Q.

После подстановки этих величин в (5.4) получаем окончательно дифференциальное уравнение объекта в виде:

(5.5)

В преобразованном по Лапласу виде это уравнение отобразится как

(Т_ар + β)φ(р) = ξ - λ, и передаточная функция одноемкостного объекта

W(p) = 1/(Т_ар + β)

Таким образом, одноемкостный объект является звеном первого порядка. В зависимости от коэффициента самовыравнивания он может быть:

При β >0 - апериодическим звеном с передаточной функцией

W(p) = k/(Тр +1), где T = Т_а/β, k = 1/β

При β = 0 - интегрирующим звеном с передаточной функцией

W(p) = 1/Т_ар

При β < 0 - неустойчивым звеном.

При расчетах систем управления иногда нет точных сведений о коэффициенте самовыравнивания. В таких случаях рассматривают объект как интегрирующее звено.

Как видно, вид звена, представляющего одноёмкостный объект, непосредственно связан с видом статических характеристик, т.е. устойчивый объект является апериодическим звеном, астатический - интегрирующим.

Простым примеров двухъёмкостного объекта является система из двух последовательно включенных ёмкостей с жидкостью (рис. 23). Дифференциальное уравнение такого объекта выводится достаточно просто, и можно показать, что он является звеном второго порядка. В данном случае можно также представить этот объект как два последовательно соединенных апериодических звена. Однако иногда параметры, характеризующие поведение сложного объекта, трудно определимы. Например, типичным случаем сложного объекта является система охлаждения ДВС, рассматриваемая как объект регулирования по температуре охлаждающей жидкости. В таких случаях, если переходную характеристику объекта можно получить экспериментальным путем, целесообразно представить его в качестве последовательного соединения апериодического звена и звена запаздывания, как показано в разделе 4.3 (рис.19)

2. Автоматические управляющие устройства

Автоматические управляющие устройства измеряют входные или выходные параметры объекта и вырабатывают управляющее воздействие таким образом, чтобы управляемый параметр сохранял заданное значение или изменялся по заданной программе. Управляющее устройство реализует один из фундаментальных принципов управления (см. раздел 2). Как показано в этом разделе, в технических системах наибольшее распространение имеет управление по отклонению управляемого параметра. При этом входным параметром для системы управления является один или несколько показателей работы объекта:

1) величина и знак отклонения текущего значения управляемого параметра от заданного значения (рассогласование) Δφ = φ - φ_з;

2

) производная (скорость изменения) рассогласования по времениdΔφ/dt;

3) интеграл величины рассогласования за время t, т.е.

В зависимости от того, как формируется управляющее воздействие управляющего устройства на объект, различаются законы управления. Соответственно этому различаются следующие виды управляющих устройств:

• релейные, реализующие нелинейный двухпозиционный закон управления;

• пропорциональные (статические, или устройства с жесткой обратной связью);

• интегральные (астатические, устройства без обратной связи);

• пропорционально-интегральные (изодромные, или устройства с исчезающей обратной связью);

• пропорционально-дифференциальные (статические устройства с предварением);

• п

  

  ропорционально-интегрально-дифференциальные (изодромные управляющие устройства с предварением).

Релейный закон управления. При таком законе управляющее воздействие не имеет промежуточных значений и изменяется практически мгновенно от нуля до максимума или обратно в моменты перехода управляемого параметра через заданные значения. Интервал между этими предельными значениями характеризуется зоной нечувствительности ε, в пределах которой управляемый параметр может иметь произвольное значение (рис. 24). Выбор величины зоны нечувствительности определяется компромиссом между допустимыми колебаниями управляемой величины и частотой переключений управляющего устройства. Очевидно, что чем меньше зона нечувствительности, тем чаще должно включаться и выключаться управляющее воздействие, что приводит к износу управляющего устройства и выходу его из строя. Такой закон управления используется в системах, где требования к точности поддержания управляемого параметра не особенно строги. В частности, такой закон управления применяется в системах поддержания заданного уровня жидкости, при управлении нагревательными или охлаждающими устройствами и пр.

Пропорциональный закон управления. В устройствах, реализующих такой закон, величина управляющего воздействия определяется как

где k_p - коэффициент усиления.

Если ξ = 1 (управляющее воздействие, приложенное к объекту, равно номинальному значению, то рассогласование Δφ достигает максимального значения, которое называют степенью неравномерности системы автоматического управления δ = Δφ_max. Из этого следует, что при пропорциональном законе управления δ = 1/ k_p, то есть такой закон управления подразумевает наличие некоторого диапазона изменений управляемого параметра. При этом каждому значению нагрузки (имея в виду, что на установившихся режимах ξ = λ) соответствует определенная величина управляемого параметра. Такая зависимость обеспечивает устойчивость системы управления. В идеальном случае управляющее воздействие появляется одновременно с появлением отклонения Δφ (рис. 25). Однако в реальных системах управляемый параметр не изменяется мгновенно. Соответственно управляющее воздействие не сразу достигает величины, уравновешивающей изменение параметра нагрузки. Вследствие этого системам управления, реализующим пропорциональный закон, свойственно недостаточное быстродействие, вследствие чего переходные процессы приобретают колебательный характер и растягиваются во времени. Кроме того, такой закон управления неприемлем в тех случаях, когда предъявляются жесткие т

ребования к диапазону изменений управляемого параметра. В последнем случае может быть использованинтегральный закон управления, при котором управляющее воздействие формируется в соответствии с формулой:

где Ти - время интегрирования.

При любом установившемся режиме производная dξ/dt = 0. Следовательно, условием существования таких режимов является нулевое отклонение управляемого параметра и степень неравномерности в системе управления, реализующей интегральный закон, равна нулю (рис.26). Недостатки этого закона управления, который реализуется путем введения в управляющее устройство интегрирующего звена (например, гидроусилителя), является еще большее, чем при пропорциональном законе, запаздывание управляющего управления в статике отсутствует зависимость между нагрузкой (управляющим воздействием) и величиной управляемого параметра, которая постоянна при любых нагрузках. Поэтому равновесие в такой системе является неопределенным, а следовательно, неустойчивым. При любом отклонении управляемого параметра от заданного значения будет вырабатываться непрерывно нарастающее управляющее воздействие, что может привести к незатухающим колебаниям системы.

П

ропорционально-интегральный закон управления(рис. 27) позволяет сочетать достоинства пропорционального и интегрального законов. Управляющее воздействие определяется уравнением:

г

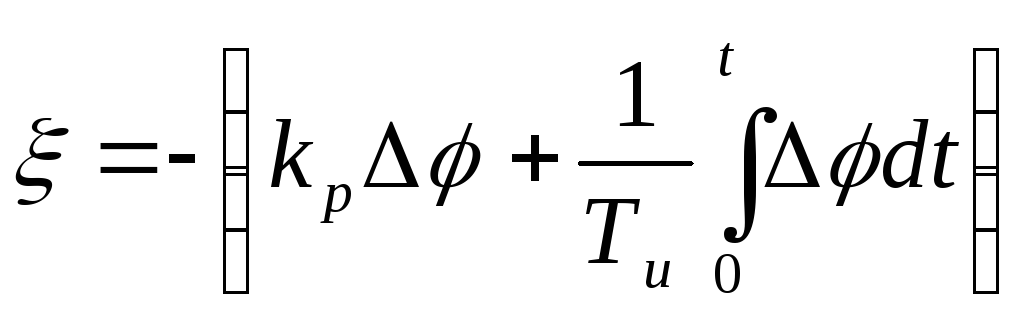
де первое слагаемое определяет пропорциональную часть (горизонтальная штриховка на рис.27), второе - интегральную (наклонная штриховка). Для установившихся режимов производныеdξ/dt = 0, dΔφ/dt =0. Дифференцирование выражения для закона управление приводит к условию существования установившегося режима Δφ =0, то есть в этом случае система поддерживает постоянное значение управляемого параметра с нулевой степенью неравномерности, как и при интегральном законе. Принципиальное отличие заключается в том, что в ходе переходного процесса к интегральной составляющей добавляется пропорциональная, благодаря которой появляется временная связь между управляемым параметром и управляющим воздействием. Благодаря этому управляющее воздействие нарастает быстрее, а система во время переходного процесса становится более устойчивой. Для реализации такого закона управления в систему должно быть введено звено, образующее исчезающую обратную связь между управляющим и управляемым параметрами. Таким свойством обладает реальное дифференцирующее звено (изодром). Управляющие устройства такого типа называются изодромными.

Пропорционально-дифференциальный закон управления (рис. 28). Управляющее воздействие определяется уравнением:

Где Т_д - время дифференцирования

Устройства такого типа называются управляющими устройствами с предварением, поскольку управляющее воздействие появляется в тот же момент, когда начинается изменение управляемого параметра. В отличие от рис. 26 и 27, зависимость управляющего воздействия от изменений управляемого параметра показана при увеличении последнего с постоянной скоростью (при ступенчатом изменении дифференциальная составляющая мгновенно достигала бы бесконечности). Управляющее воздействие является суммой двух составляющих: пропорциональной (наклонная штриховка на рис. 28) и дифференциальной (вертикальная штриховка). Последняя имеет постоянное значение при неизменной скорости изменения управляемого параметра и обращается в

Рис. 28

ноль при его постоянной величине. При установившемся режиме дифференциальная установившемся режиме дифференциальная составляющая равна нулю, и любой постоянной нагрузке соответствует определенная величина управляемого параметра. Для получения такого закона управления необходимо в измерительное устройство системы управления ввести дифференцирующее звено, включенное параллельно основной (пропорциональной) части. Аналогичного результата можно достичь, подавая на вход исполнительной части системы величину, пропорциональную производной управляемого параметра (например, параметр нагрузки). Такое управляющее устройство называют двухимпульсным. Рассмотренный закон управления обеспечивает устойчивость системы, ее быстродействие, но не допускает работу с нулевой неравномерностью.

Пропорционально-дифференциально-интегральный закон управления в соответствии с формулой сочетает достоинства всех вышеперечисленных законов, то есть позволяет осуществить устойчиво работающую систему управления, обеспечивающую нулевую неравномерность на установившихся режимах и одновременно высокое качество управления в динамике, то есть небольшое время переходного процесса и минимальные динамические отклонения управляемого параметра.

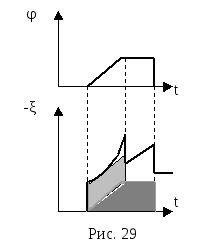
Графически величина управляющего воздействия ξ при изменении управляемого параметра φ показана сплошной линией на рис. 29. Дифференциальная составляющая (горизонтальная штриховка) существует только на участке нарастания управляемого параметра. Пропорциональная составляющая (наклонная штриховка) изменяется в соответствии с изменением φ. Равновесный режим восстанавливается при Δφ = 0 и ξ = λ. Для реализации такого сложного закона управления требуется, чтобы на вход исполнительного устройства системы управления подавалась сумма параметров, соответствующих управляемому параметру, его производной и интегралу. Наиболее просто это осуществляется в электронных регуляторах, где операции дифференцирования и интегрирования выполняются с помощью электронных схем или микропроцессоров. В этом случае предусматривается настройка постоянных интегрирования и дифференцирования, что позволяет подбирать необходимый закон изменения управляющего воздействия применительно к требованиям конкретной установки.

Устройства, создаваемые на основе пересиленных законов управления, обычно называют регуляторами. В название регулятора вводится сокращенное обозначение закона управления, например, П-регулятор, ПД-регулятор и т.д.

6. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИСТЕМ УПРАВЛЕНИЯ

С

татические и динамические свойства системы управления определяются решением дифференциального уравнения (3.4). Для линейной системы при ступенчатом изменении входного параметра (нагрузки или управляющего воздействия) это решение сводится к (4.1). Первое слагаемоеВ(0)/А(0) получаем подстановкой нуля вместо р в числитель и знаменатель передаточной функции системы W(p). Эта величина не зависит от времени и представляет собой новое установившееся значение управляемого параметра. При нулевых начальных условиях (а именно такими полагаются начальные условия при выводе передаточной функции) и изменении входного параметра от 0 до 1 это будет соответствовать степени неравномерности системы δ. Этот параметр называют также статической ошибкой или статической погрешностью системы управления. Последующие слагаемые в формуле (4.1) представляют собой функции времени, которые в совокупности образуют переходный процесс. Для каждого момента времени их сумма образует величину φ_пер (рис. 30). От характера изменения и численных значений функции φ_пер (t) зависят такие жизненно важные для практики параметры системы управления, как ее устойчивость, величина динамических "забросов" управляемого параметра и длительность переходного процесса.

1. Устойчивость системы автоматического управления

Как показано в разделе 4 (формула 4.1), переходная характеристика представляет собой сумму, в которой каждое из слагаемых является функцией времени, протекание которой определяется одним из корней характеристического уравнения А(р) = 0. Понятие устойчивости системы в строгой формулировке достаточно сложно и громоздко. С практической точки зрения устойчивой можно считать систему, которая, будучи выведена из равновесия, восстанавливает исходный установившийся режим или переходит к новому равновесному режиму. Важно отметить, что понятие устойчивости не касается длительности переходного процесс или максимальных отклонений управляемого параметра в динамике. Следует лишь убедиться, что переменная часть переходной характеристики стремится к нулю.

Чтобы определить, устойчива ли система, нет необходимос­ти решать характеристическое уравнение и оп­ределять его корни. Выясним, какие свойства корней необходи­мы и достаточны для того, чтобы система была устойчивой.

Корни могут быть вещест­венными, комплексными и чисто мнимыми.

Вещественный корень. Пусть один из корней, например р₁ , является вещественным. Тогда слагаемое, определяемое этим корнем в ре­шении, будет представлять собой экспоненту. Если он отрицательный (р₁ = -α), то ему соответствует формула С₁ ехр(-α,t) . Очевидно, что при t → ∞ этот член будет затухать.

При р₁ = +α получится расходящийся процесс (рис. 31.а).

Комплексные корни всегда попарно сопряженные. При отрицательной вещественной части два корня, например, р₁ и р₂ , будут иметь вид р_1,2 = -α ± iω. В этом случае слагаемые в решении, определяемые корнями, мо­гут быть представлены в виде С₁ еxp [(-α+iω)t] +C₂ еxp [(-α-iω)t]. Константы C₁ и C₂ являются сопряженными комплексными числами, которые в полярной форме можно представить как

C₁ = 0,5 R exp (iυ)

C₂ = 0,5 R exp (-iυ)

В соответствии с этим пара слагаемых, соответствующих данной паре корней, также образует комплексную сопряженную пару

φ₁ = 0,5 R exp (-αt)exp[ i(ωt +υ)]

φ₂ = 0,5 R exp (-αt)exp[- i(ωt +υ)]

Согласно формуле Эйлера, exp(+iωt) = cosωt + isinωt, поэтому суммирование дает для пары сопряженных корней

φ ₌ φ_{1 +} φ₂ = R еxp (-αt)cos(ωt +υ)

Таким образом, пара комплексных сопряженных корней с отрицательной вещественной частью дает в решении дифференциального уравнения слагаемое, представляющее затухающие колебания. При положительной вещественной части колебания будут расходящимися (рис. 31 б, в).

Пара чисто мнимых корней (при нулевой вещественной части) дает незатухающие колебания с постоянной амплитудой (рис. 31 в).

Таким образом, условием того, что переходный процесс будет сходящимся, а система - устойчивой, является отрицательное значение вещественных корней и вещественной части комплексных корней характеристического уравнения.

В

сю совокупность корней характеристического уравнения можно представить на комплексной плоскости с координатами (α,iω) (рис. 32). При этом действительные корни расположатся на оси абсцисс, чисто мнимые будут представлены парами, расположенными по оси ординат и при равном расстоянии точек от начала координат, комплексные корни также расположатся в виде пар точек, симметричных относительно оси абсцисс. По расположению относительно мнимой оси корни различаются на правые и левые.

Поскольку корни, имеющие отрицательную вещественную часть, располагаются в левой полуплоскости, то необходимое и достаточное условие устойчивости системы можно сформулировать так: линейная система управления устойчива, если все корни ее характеристического уравнения - левые. Мнимая ось при этом является границей устойчивости.