
Лекции УТС корр2014
.pdf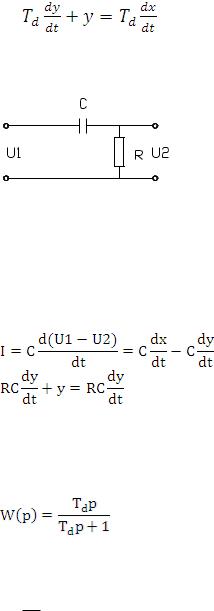
21
Постоянная дифференцирования T = C. Если на полностью заряженный конденсатор подать скачек напряжения, между обкладками проскочит искра, и сила тока мгновенно увеличится до очень большой величины.
Преобразование по Лапласу отображает дифференциальное уравнение звена в
виде :
Y(P)=TdX(P),
передаточная функция W(p) = Tdp.
Реальное дифференциальное звено
В системах управления используется реальное дифференциальное звено, описываемое уравнением:
Электрический аналог включает RC цепь с последовательным соединением емкости и активного сопротивления (рис. 15):
Рис. 15
Входной сигнал –напряжение U1. Выходной сигнал – напряжение U2 на сопротивлении R.
U2=IR
Ток в цепи конденсатора:
Постоянная дифференцирования Тd=RC (на графике переходной функции соответствует месту пересечения касательной, проведенной к графику в начале координат, с осью времени).
Интегрирующее звено
Дифференциальное уравнение интегрирующего звена:
dy
T и dt x ,
где Ти – время интегрирования Примером интегрального звена является гидроусилитель (рис. 16)
Скорость изменения координаты y (перемещения поршня рабочего цилиндра) будет пропорциональной входной координате х ( перемещению золотника).
Переходная характеристика получается как результат интегрирования:

22
xt
y
T и
График переходной функции в этом случае представляет собой прямую, уходящую в бесконечность. Интегрирующее звено не обладает способностью возвращаться к установившемуся режиму при единичном возмущении на входе.
Данное звено – астатическое. Передаточная функция:
Рис.16
Звено запаздывания
Звену запаздывания соответствует уравнение:
y(t) =x(t –η),
где η – время запаздывания. Передаточная функция:
Колебательное звено
Физическая структура такого звена характеризуется наличием двух аккумулирующих емкостей. Аккумуляторы обладают возможностью, запасая энергию, периодически обмениваться ею.. Механическая система, состоящая из массы, пружины и демпфирующего устройства в виде поршня , перемещающегося в цилиндре с маслом, также относится к колебательному звену, если коэффициент затухания меньше 1.
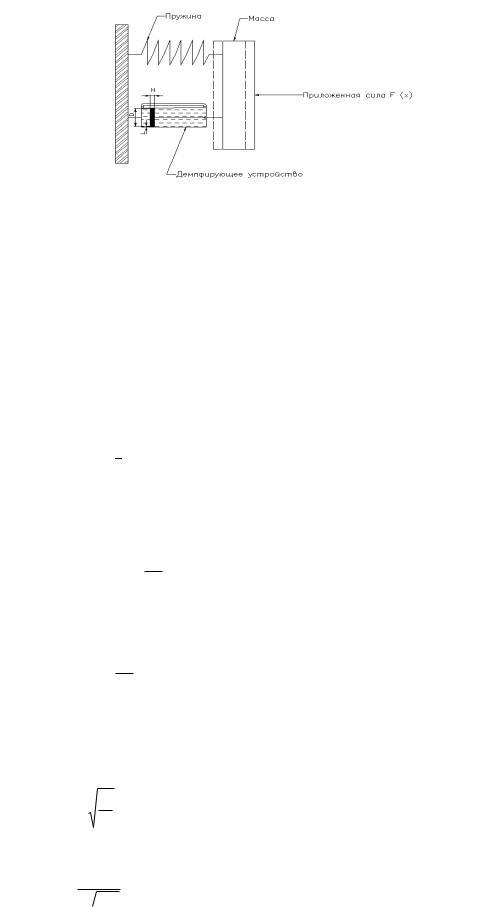
23
Примером системы второго порядка является пружинная система с демпфированием (рис.17).
Рис.17 Система включает три основных элемента: массу, пружину и
демпфирующее устройство – поршень, перемещающийся в цилиндре, заполненном маслом. Входным сигналом является сила F, выходным – длина пружины y
.Результирующая сила, действующая на массу m, равна разности приложенной силы F, силы упругости пружины (от растяжения или сжатия), и силы демпфирующего устройства.
Сила упругости пружины пропорциональна изменению ее длины y, т.е. ее можно представить в виде ky, где k – коэффициент жесткости пружины.
Сила демпфирующего устройства будет пропорциональна скорости
3 2
перемещенияF 7поршня.854 10 , т.е.мее можно представить в виде c(dy/dt), где с –константа.
1
c Fп
l
где μ – коэффициент динамической вязкости жидкости, l – зазор между трущимися поверхностями, Fп – поверхность трения.
Результирующая сила R, действующая на массу m, будет равна:
R F ky c dy dt
По второму закону Ньютона эта сила заставляет массу двигаться с ускорением. Т.к. ускорение – производная скорости, а скорость – производная перемещения (dy/dt)
F ky |
c |
dy |
m |
dy 2 |
||||
dt |
dt |
2 |
||||||
|
|
|
|
|||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
m |
dy 2 |
c |
|
dy |
ky |
F |
||
|
|
|
||||||
2 |
|
|
|
|
|
|
||
dt dt
В случае отсутствия демпфирующего устройства масса, прикрепленная к концу пружины,, будет колебаться с собственной частотой
п
k
m
Колебательные системы характеризуются коэффициентом затухания ζ, определяемым как:
с
2  mk
mk
Тогда уравнение движения системы приобретает вид:

24
1 |
|
d 2 y |
|
2 |
|
dy |
|
y |
1 |
F |
2 |
|
dt 2 |
п |
|
dt |
k |
||||
|
|
|
|
|
|
|||||
п |
|
|
|
|
|
|
|
|
|
|
5.6 Применение преобразования Лапласа для расчета характеристик звена второго порядка
Колебательное звено относится к динамическим звеньям второго порядка и описывается дифференциальным уравнением:
a 2 |
d 2 y |
a 1 |
dy |
a |
|
y |
b 0 x |
|
|
|
|
0 |
|||||
dt |
2 |
dt |
||||||
|
|
|
|
|
|
|
||
Как следует из правил преобразования по Лапласу, вторая производная функции y(t) преобразуется в трехчлен:
p 2 Y(p) - y(0) - p d y ( 0 ) , dt
первая производная преобразуется в двучлен:
,
где y(0) – значение функции при t = 0.
Вычитание двух функций а0y – b0x преобразуется в a0Y(p)-b0X(p).
Если при t = 0 y(0) = 0 и d y ( 0 ) 0 , дифференциальное уравнение преобразуется
dt
в алгебраическое:
a2p2Y(p)+ a1pY(p)+a0Y(p)=b0X(p)
Передаточная функция:
W ( p ) |
Y ( p ) |
|
b |
0 |
|
b |
0 / a 0 |
|
X ( p ) |
a 2 p 2 a 1 p a 0 |
a 2 / a 0 p 2 a 1 / a 0 p 1 |
||||||
|
|
|
||||||
Учитывая, что b0/a0 – это передаточная функция в статическом режиме W,
W ( p )
W
a 2 / a 0 p 2 a 1 / a 0 p 1
Дальнейшие преобразования сводятся к искусству разложения многочлена на множители. Принимая во внимание, что звено второго порядка может быть записано через величины собственной частоты колебания ω и коэффициент затухания ζ,
W ( p )
W
(1 / п2 ) p 2 ( 2 / п ) p 1
Рассмотрим выходной сигнал при скачкообразном сигнале на входе.
Y ( p ) W ( p ) X ( p )
Так как X(p) = 1/p,
Y ( p )
W
[(1 / п2 ) p 2 ( 2 / п ) p 1 ]p
После преобразований выражение принимает следующий вид:
Y ( p ) |
1 |
|
|
|
p п |
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
||||||
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
2 |
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
2 |
|
||||||
|
p |
|
|
( p |
п ) |
|
п (1 |
|
|
) |
|
( p |
п ) |
|
|
п |
(1 |
|
|
) |
||||||
При критическом затухании, т.е. при ζ = 1, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Y ( p ) |
1 |
|
|
1 |
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
( p п ) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
p |
|
|
( p п ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Используя таблицу преобразований Лапласа, конвертируем решение, полученное в Лапласовой форме, в функцию, зависящую от времени:
25
y W (1 e п t п te п t ) W [1 e п t (1 п t )]
5.7. Передаточные функции при соединении звеньев в различных вариантах
Различают три основных варианта соединения звеньев:
-последовательное
-параллельное
-встречно-параллельное (обратная связь)
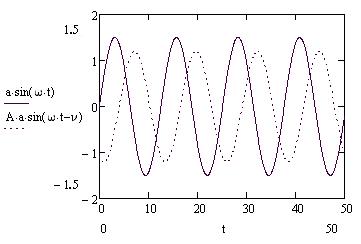
При последовательном соединении звенья образуют разомкнутую цепь, в которой во всех промежуточных звеньях выходной параметр предыдущего звена является входным для последующего. Схема последовательного соединения показана на рис. 18.
Рис. 18 Передаточная функция цепочки последовательно соединенных звеньев равна
произведению передаточных функций отдельных звеньев:
W(p) = Y(p)/X(p) = W1(p)·W2(p) ··Wk(p)
При параллельном соединении входной параметр одинаков для всех звеньев, а выходные параметры каждого из них суммируются. Схема параллельного соединения показана на рис. 19.
Рис19
Согласно определению y(t) = y1(t) +y2(t)+…+ yk(t) , тогда исходя из свойства преобразования Лапласа Y(p) = Y1(p)+ Y2(p)+…+ Yk(p).
Передаточной функцией системы параллельно соединенных звеньев является сумма передаточных функций отдельных звеньев:
W(p) = W1(p)+ W2(p)+…+Wk(p).
Отсюда следует важное свойство: параллельно соединяя простые звенья можно откорректировать какие-либо нежелательные свойства основного передающего канала.
При встречно-параллельном соединении, образующем замкнутую цепь, выходной параметр y охватываемого звена W1(p) передается на вход того же звена, но уже в преобразованном виде (рис. 20).
Рис. 20 В системах автоматического управления используется отрицательная обратная
связь, когда на вход подается сигнал противоположного отклонению y знака. Входным параметром для звена W1(p) разность x - y1. В преобразованном по Лапласу виде
Y(p) = [X(p) – Y1(P)]·W1(p)
В свою очередь
26
Y1(P)= Y(p) · W2(p)
Y(p) = [X(p) – Y(p) · W2(p)]· W1(p) = X(p) ·W1(p) - Y(p) · W2(p)·W1(p) Y(p)[1+ W2(p)·W1(p)] = X(p) ·W1(p)
W ( p ) |
Y ( p ) |
|
W 1 ( p ) |
|
X ( p ) |
1 W 1 ( p ) W 2 ( p ) |
|||
|
|
Следует иметь в виду, что и прямая, и обратная цепь могут состоять из нескольких звеньев. Тогда предварительно рассчитывается передаточная функция прямой и обратной цепи. Передаточная функция системы с обратной связью равна дроби, числитель которой - передаточная функция прямой цепи, а знаменатель равен сумме единицы и произведению передаточных функций прямой и обратной цепи.
5.8 Частотный метод изучения динамики звена
Ранее были рассмотрены переходные характеристики динамических звеньев, полученные при единичном скачке сигнала на входе. Вторым методом изучения динамики звеньев и систем управления является частотный метод, при котором на вход звена или системы подается гармоническое колебание входной координаты:
x = a sinωt
В этом случае спустя некоторое время на выходе будет записано колебательное изменение во времени выходной координаты. Однако фаза и амплитуда выходной координаты будут отличаться от амплитуды и фазы колебаний входной координаты.
y = Aa sin(ωt-υ),
где А – степень искажения амплитуды, υ – фаза отставания (опережения). На рис. 21 показано изменение во времени входного и выходного сигнала для конкретных значений частоты, степени искажения амплитуды и фазы отставания.
0.52
a 1.5 A 0.8
Рис. 21 Физически полученный результат означает, что благодаря инерционным и
демпфирующим свойствам звена подаваемое на его вход колебание проводится к выходу в несколько искаженном виде. В теоретическом дифференциальном звене сигнал на выходе имеет опережение по фазе на π/2.
27
Сопоставляя степень искажения колебаний при их прохождении через разные звенья и системы при разной частоте, можно судить о динамических свойствах этих звеньев или систем.
Гармоническое колебание можно характеризовать и с помощью изменения во времени проекции радиусвектора некоторого комплексного числа:
На плоскости комплексного переменного число z представляет собой точку, характеризуемую координатами: по оси вещественных чисел u= acos ωt и по оси мнимых чисел υ= asin ωt, где а –модуль радиус-вектора, построенного из начала координат, ωt – аргумент. В комплексной записи содержатся характеристики колебания а и ω.
Можно воспользоваться записью колебаний в форме Эйлера: z = a(cos ωt + jsin ωt) = aejωt
Используя такую форму записи, определим выражение для комплексного передаточного коэффициента kj, с помощью которого можно изучать амплитудно-фазовые частотные характеристики. Если x = aejωt, y = A aej(ωt-υ) , то
|
|
|
y |
|
aAe |
j ( t ) |
Ae j |
|
k |
j |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
a е j t |
|
|||
|
|
|
|
|
||||
В выражение для kj входит как модуль величина отношения амплитуд А и как аргумент – фаза отставания υ. Сопоставляя значения kj, сравнивают характеристики различных звеньев и систем при одинаковой частоте. Меняя частоту, можно установить характер изменения kj, т.е. характер изменения динамической проводимости звена или системы. Может быть построена кривая – геометрическое место точек kj для разных υ на плоскости комплексного переменного. Такая кривая носит название амплитудно-фазовой характеристики АФХ. Первоначально частотный метод использовался в основном в экспериментальных исследованиях динамических характеристик систем регулирования.
Располагая дифференциальными уравнения ми звеньев, можно перейти от них к частотным зависимостям и проводить аналитические исследования систем.
5.9 Последовательность составления математического описания системы управления
Для исследования свойств системы управления необходимо составить ее математическую модель в виде дифференциального уравнения:
a 0 |
d n y |
a 1 |
d n 1 y |
|
a n 1 |
dy |
a n y |
b 0 |
d m x |
b 1 |
d m 1 x |
|
b m 1 |
dx |
b m x |
5.1, |
||||
dt |
n |
dt |
n 1 |
dt |
dt |
m |
dt |
m 1 |
dt |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Статические и динамические свойства системы управления определяются решением этого уравнения.
Однако в практике проектирования и анализа систем управления составить и решить такое уравнение во многих случаях не представляется возможным. Поэтому составляют и исследуют отображение в Лапласовой форме данного уравнения.
Первым этапом разработки математической модели является составление структурной схемы, представляющей собой совокупность динамических звеньев. Порядок разработки структурной схемы следующий:
1.Анализируется конструктивная схема, показывающая основные элементы системы и взаимосвязи между ними.
2.На основании конструктивной схемы изображается функциональная схема, на которой отдельные элементы системы и связи между ними представляются в упрощенном виде.
3.Определяется вид математических зависимостей, описывающих отдельные элементы функциональной схемы. Исходя из вида полученных зависимостей, функциональные элементы заменяют динамическими звеньями. При этом один функциональный элемент может заменяться несколькими динамическими звеньями.
28
После составления структурной схемы приступают к задаче составления дифференциального уравнения системы управления. Порядок действий следующий.
1.Выводятся дифференциальные уравнения звеньев. При этом прежде всего выявляется физический закон, определяющий поведение данного элемента системы: например, закон сохранения вещества, закон сохранения энергии, равновесия сил, равновесия крутящих моментов, равновесия электродвижущих сип и др. Математическое выражение соответствующего физического закона является исходным дифференциальным уравнением данного элемента системы управления, применительно к дизельным установкам – это элемент системы автоматического регулирования (САР).
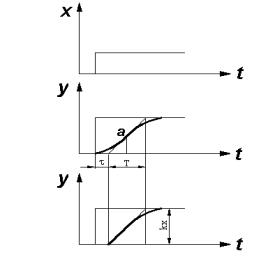
2.Полученное дифференциальное уравнение позволяет классифицировать звено (линейное, нелинейное, порядок звена) и определить его передаточную функцию. Желательно свести систему к совокупности типовых звеньев, не имеющих высокого порядка и по возможности линейных. С этой целью производится линеаризация полученных уравнений. На практике для линеаризации чаще всего применяют способ, при котором все криволинейные зависимости в переходных характеристиках звеньев заменяются прямыми, по касательной в соответствующей точке кривой. Линеаризация допустима для гладкой непрерывной функции. Возможна также замена сложного звена соединением двух и более простых звеньев. Например, сложное звено второго порядка может быть представлено как последовательное соединение звена запаздывания и звена первого порядка (рис. 22). Для этого через точку перегиба графика переходной функции a проводят касательную, которая затем рассматривается как касательная к графику переходной функции
апериодического звена первого порядка. Передаточная функция звена чистого запаздывания W1(p) = e-ηp. Передаточная функция апериодического звена первого порядка:
W 2 |
( p ) |
|
k |
|
, передаточная функция последовательно соединенных звеньев |
|||||
|
|
|
||||||||
|
|
|
||||||||
|
|
Tp |
|
1 |
|
|
|
|
||
равна их произведению: W ( p ) |
|
k |
|
e |
p |
|||||
|
|
|
||||||||
|
|
|
|
|||||||
|
|
|
|
|
|
Tp |
|
1 |
|
|

29
Рис. 22. Пример замены сложного динамического звена на последовательное соединение звена запаздывания и а периодического звена первого порядка
3.На основании структурной схемы определяется передаточная функция замкнутого контура САУ как комбинация передаточных функций звеньев, соединенных последовательно, параллельно и в виде обратной связи.
4.Задавая единичный скачек входного параметра, получают отображение выходного параметра в виде алгебраической дроби:
B ( p )
Y ( p )
pA ( p )
5. Используя свойства преобразования Лапласа ( теорему о пределах и теорему разложения, получают временную функцию y(t) в виде формулы:
|
B ( 0 ) |
n |
B ( p k ) |
|
|
y ( t ) x |
x |
e p k t , |
|||
A ( 0 ) |
p k A ( p k ) |
||||
|
1 |
|
|||
|
|
|
|
где pk – корни характеристического уравнения A(p) = 0, n – степень полинома
первое слагаемое B(0)/A(0) получают подстановкой 0 вместо Р в числитель и знаменатель передаточной функции системы W(p).
Следует иметь в виду, что разложение в приведенную выше формулу возможно,
если функция Y ( p ) |
B ( p ) |
дробно-рациональна, причем степень полинома |
|
|
|||
pA ( p ) |
|||
|
|
числителя меньше степени полинома знаменателя.
6. Виды регуляторов
Как было показано ранее, наиболее распространенная задача управления – поддержание заданных законов изменения во времени параметров объекта (регулирование). Устройство, осуществляющее управляющее воздействие, называется регулятором. Регуляторы включают в себя простые динамические звенья, комбинируя которые добиваются требуемых переходных характеристик системы управления при случайных воздействиях и изменении нагрузки. При этом входным параметром для регулятора является один или несколько показателей работы объекта:
-величина и знак отклонения управляемого параметра от заданного значения
(рассогласование) Δθ = θ-θ0
-производная (скорость рассогласования по времени) d ,
dt
t
- интеграл величины рассогласования во времени dt .
0
В зависимости от того, как формируется управляющее воздействие, различают законы управления и соответствующие им регуляторы:
-релейные, реализующие нелинейный двухпозиционный закон управления
-пропорциональные (статические, или устройства с жесткой обратной связью)
-интегральные (астатические, устройства без обратной связи)
-пропорционально-интегральные, (изодромные, или устройства с исчезающей обратной связью)

30
-пропорционально-дифференциальные (статические устройства с предварением)
-пропорционально-интегрально-дифференциальные (изодромные устройства с
предварением).
Применительно к установкам с ДВС релейный закон управления реализуется в системах регулирования давления и уровня, с помощью двухпозиционного реле включаются и отключаются насосы и компрессоры. Чтобы избежать слишком частых пусков и остановок механизмов устанавливается определенный интервал между значениями управляемого параметра, соответствующего включению и отключению реле (зона нечувствительности).
Остальные законы управления реализуются в основном в регуляторах скорости. График регулирования по релейному закону представлен на рис. 23.
Рис.23 Пропорцинальные регуляторы вырабатывают управляющее воздействие в виде
линейной зависимости от отклонения от отклонения регулируемого параметра:
ζ = - kpΔθ,
где kp – коэффициент усиления по регуляторному каналу.
Зависимость управляющего воздействия от отклонения регулируемого параметра показана на рис.24.
Рис.24 Так как в установившемся режиме определенной нагрузке должно соответствовать
определенное положение регулирующего устройства, невозможно осуществлять регулирование во всем диапазоне нагрузок без определенной ошибки, называемой статизмом регулятора:
|
max |
|
( max |
min ) / min |
|
( max |
min ) |
|
max |
( ном 0 ) / ном |
min |
||||||
|
|
|
||||||
