5.5 Примеры динамических звеньев.

Кроме приведенной выше классификации звеньев по уровню реакции на время существует классификация звеньев по их назначению в системе управления.

Усилительное звено

Усилительное звено – устройство, повышающее значение некоторой величины за счет энергии постороннего источника с постоянным коэффициентом передачи.

Усилители широко применяются в автоматике в измерительных устройствах и при передаче управляющего сигнала к исполнительному механизму. Простейшим примером усилительного звена является шестереночная передача, увеличивающая угловую частоту вращения.

Применение шестереночных передач в приводах центробежных регуляторов скорости позволяет увеличить силу регуляторного воздействия до требуемого уровня без увеличения размеров исполнительного механизма. Как известно, центробежная сила при постоянной массе и радиусе вращения зависит от квадрата угловой скорости: Fцб = m·r·ω2, поэтому при увеличении частоты вращения оси регулятора скорости необходимое для перемещения рейки топливного насоса усилие будет отбираться от двигателя без выхода отклонения его частоты вращения за допустимые пределы.

Другими примерами усилительного звена являются трансформаторы напряжения и тока.

Усилительное звено относится к динамическим звеньям нулевого порядка и описывается уравнением: y(t)=kx(t) .

Апериодическое (инерционное) звено первого порядка.

Такое звено описывается дифференциальным уравнением:

,

где T – постоянная времени звена, а k – коэффициент усиления. Электрическим аналогом такого звена является цепочка с сопротивлением R и емкостью С (рис. 14).

Рис. 14 Апериодическое (инерционное) звено

Входной параметр U1 = x. выходной U2 = y. Если изменится входное напряжение, появится ток в цепи конденсатора. Выходное напряжение будет связано с входным соотношением: U1 = U2+IR. Сила тока в цепи конденсатора:

При подстановке получаем:

Постоянная времени звена T = RC, коэффициент усиления k = 1.

Другим примером апериодического звена является уже рассмотренный нами пример чувствительного элемента измерителя температуры. Переходная характеристика уже рассмотрена выше и представляет собой экспоненциальную зависимость

y= kx(1-e-t/T)

Передаточная функция:

Дифференциальное звено.

Дифференциальное звено описывается уравнением:

,

где Td – постоянная дифференцирования. При мгновенном ступенчатом изменении входного параметра выходной параметр тоже мгновенно возрастает до бесконечности и тут же снижается до 0, т.е. при единичном скачке входного параметра дифференциальное звено выдает одиночный импульс. Если входная величина меняется с постоянной скоростью, на выходе должен быть постоянный сигнал. В реальности такое звено сложно реализовать.

Электрическим аналогом является цепочка с конденсатором С, если входным параметром считать напряжение, а выходным – силу тока.

Постоянная дифференцирования T = C. Если на полностью заряженный конденсатор подать скачек напряжения, между обкладками проскочит искра, и сила тока мгновенно увеличится до очень большой величины.

Преобразование по Лапласу отображает дифференциальное уравнение звена в виде :

Y(P)=TdX(P),

передаточная функция W(p) = Tdp.

Реальное дифференциальное звено

В системах управления используется реальное дифференциальное звено, описываемое уравнением:

Электрический аналог включает RC цепь с последовательным соединением емкости и активного сопротивления (рис. 15):

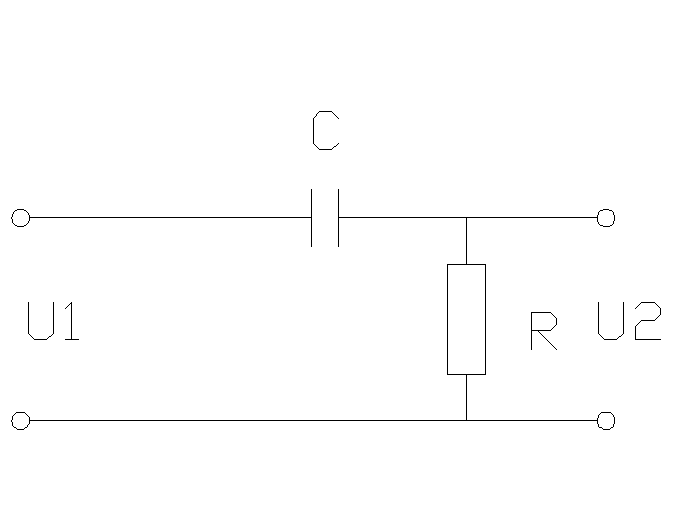
Рис. 15

Входной сигнал –напряжение U1. Выходной сигнал – напряжение U2 на сопротивлении R.

U2=IR

Ток в цепи конденсатора:

Постоянная дифференцирования Тd=RC (на графике переходной функции соответствует месту пересечения касательной, проведенной к графику в начале координат, с осью времени).

Интегрирующее звено

Дифференциальное уравнение интегрирующего звена:

,

где Ти – время интегрирования

Примером интегрального звена является гидроусилитель (рис. 16)

Скорость изменения координаты y (перемещения поршня рабочего цилиндра) будет пропорциональной входной координате х ( перемещению золотника).

Переходная характеристика получается как результат интегрирования:

График переходной функции в этом случае представляет собой прямую, уходящую в бесконечность. Интегрирующее звено не обладает способностью возвращаться к установившемуся режиму при единичном возмущении на входе.

Данное звено – астатическое. Передаточная функция:

Рис.16

Звено запаздывания

Звену запаздывания соответствует уравнение:

y(t) =x(t –τ),

где τ – время запаздывания.

Передаточная функция:

Колебательное звено

Физическая структура такого звена характеризуется наличием двух аккумулирующих емкостей. Аккумуляторы обладают возможностью, запасая энергию, периодически обмениваться ею.. Механическая система, состоящая из массы, пружины и демпфирующего устройства в виде поршня , перемещающегося в цилиндре с маслом, также относится к колебательному звену, если коэффициент затухания меньше 1.

Примером системы второго порядка является пружинная система с демпфированием (рис.17).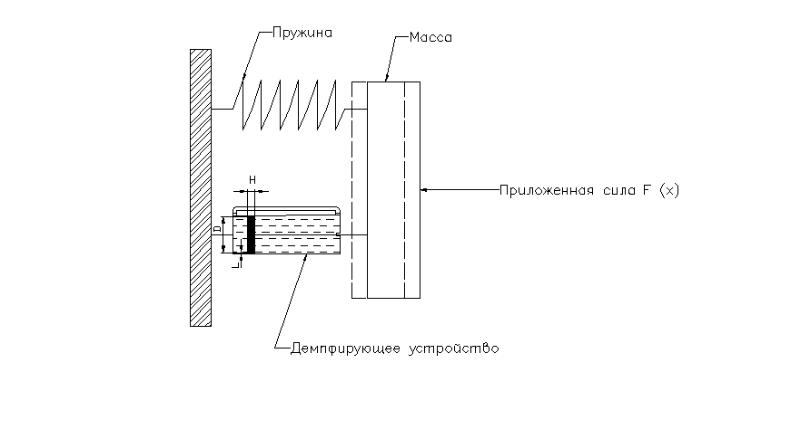

Рис.17

Система включает три основных элемента: массу, пружину и демпфирующее устройство – поршень, перемещающийся в цилиндре, заполненном маслом. Входным сигналом является сила F, выходным – длина пружины y .Результирующая сила, действующая на массу m, равна разности приложенной силы F, силы упругости пружины (от растяжения или сжатия), и силы демпфирующего устройства.

Сила упругости пружины пропорциональна изменению ее длины y, т.е. ее можно представить в виде ky, где k – коэффициент жесткости пружины.

Сила демпфирующего устройства будет пропорциональна скорости перемещения поршня, т.е. ее можно представить в виде c(dy/dt), где с –константа.

где μ – коэффициент динамической вязкости жидкости, l – зазор между трущимися поверхностями, Fп – поверхность трения.

Результирующая сила R, действующая на массу m, будет равна:

По второму закону Ньютона эта сила заставляет массу двигаться с ускорением. Т.к. ускорение – производная скорости, а скорость – производная перемещения (dy/dt)

В случае отсутствия демпфирующего устройства масса, прикрепленная к концу пружины,, будет колебаться с собственной частотой

Колебательные системы характеризуются коэффициентом затухания σ, определяемым как:

Тогда уравнение движения системы приобретает вид: