8.3 Графическая иллюстрация теорем Ляпунова

В общем виде решение уравнения 8.11 представляет собой функцию:

y – C₁e^r1t + C₂e^r2t +…+ C_ne^rnt, 8.13

где r₁,r₂, …r_n– корни характеристического уравнения, С_i– постоянные интегрирования.

Как известно, устойчивость системы определяется устойчивостью ее свободного движения. Следовательно, для устойчивости системы необходимо, чтобы при t→ ∞y→0. На рис. 29 представлены графики функцийe^rt при различных значениях корней уравнения – вещественных, комплексных и чисто мнимых. Комплексные корни дают составляющую вида:

,

где С_kи ψ_kпостоянные интегрирования. При построении графика принято: ω =5, ρ=1, ψ=1.

Рис. 29

При вещественных отрицательных корнях функция стремится к нулю , при положительных – стремится к бесконечности. При комплексных корнях имеет место колебательный процесс. Если вещественная часть отрицательная, колебания затухающие, если положительная – амплитуда колебаний возрастает с течением времени. При чисто мнимых корнях колебания происходят при постоянной амплитуде. Независимо от численных значений коэффициентов С_i, присутствие хотя бы одного корня с положительной вещественной частью приводит к неустойчивости системы.

Таким образом, исследование корней характеристического уравнения является достаточным для оценки устойчивости системы автоматического управления. Однако прямое исследование сравнительно просто может быть выполнено лишь для уравнений первого и второго порядка. Уже для уравнений третьего и четвертого порядка прямое определение корней представляет значительные трудности.

Вместе с тем, чтобы ответить на вопрос об устойчивости системы, достаточно знать не сами корни, а только знаки вещественных частей. Поэтому можно произвести анализ с помощью специальных привил, называемых критериями устойчивости и позволяющих установить факт существования всех отрицательных корней.

8.4 Алгебраические критерии устойчивости (критерии Гурвица)

Система регулирования, для которой составлено характеристическое уравнение 8.12:

a₀ pⁿ + a₁ p^n-1 +… + a_n-1 p +a_n =0,

будет устойчива, если:

1. Все коэффициенты характеристического уравнения окажутся положительными.

2. Все определители, составленные из коэффициентов характеристического уравнения по показанной ниже схеме, окажутся положительными:

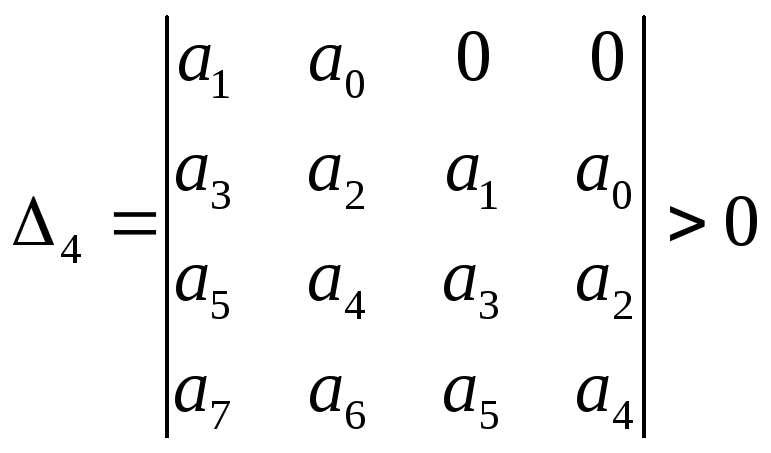и т.д.

Схема составления определителей Гурвица такова. В соответствии с порядком определителя (его номером) вначале записывают главную диагональ, идущую слева вниз направо: от коэффициента а₁до коэффициента а_{n ,} гдеn– номер определителя. Все строки дополняют коэффициентами до их общего числа, равного номеру определителя. При этом вправо от написанного элемента строки ставят коэффициенты с убывающими номерами индексов, а влево – с возрастающими номерами индексов. Если в уравнении 8.12 не содержатся коэффициенты с большим или меньшим индексом, в соответствующем месте строки ставится 0.

8.5 Частотные критерии устойчивости

На плоскости комплексного переменного корни характеристического уравнения устойчивой системы при свободном движении должны располагаться в левой полуплоскости, что соответствует отрицательной вещественной части корней.

Пользуясь представлениями частотного метода исследования, можно путем несложных преобразований характеристического уравнения, без нахождения самих корней решить вопрос об их расположении в той или иной полуплоскости комплексного переменного.

Критерий Михайлова

Если имеется характеристическое уравнение вида 8.12 и корню rпридается чисто мнимое значениеr=jω, что соответствует нахождению системы на границе устойчивости, то полином характеристического уравнения окажется сведенным к некоторому комплексному числу:

F(jω) =u(ω) +jv(ω), где

u(ω) = a_n - a_n-2 ω² - a_n-4 ω⁴ - …;

v(ω) = a_n-1 ω - a_n-3 ω² - a_n-5 ω³ - …

На плоскости комплексного переменного число F(jω) может быть отмечено соответствующей точкой.

Если изменять величину ωот 0 до + ∞, комплексное числоF(jω) составит на плоскости комплексного переменного некоторое геометрическое место точек –годограф Михайлова.

Система автоматического управления устойчива, если годограф Михайлова при изменении ωот 0 до + ∞ обходит последовательно в положительном направлении (против часовой стрелки)nквадрантов комплексной плоскости, гдеn– степень характеристического уравнения данной системы.

Доказательство критерия основывается на том, что при изменении ωот 0 до + ∞ радиус-вектор, построенный из начала координат до точки, соответствующей данному корню (в общем случае – комплексному), поворачивается в положительном направлении на угол π/2. Для всех отрицательных корней общий угол поворота годографа равенnπ/2. Следовательно, годограф устойчивой системы должен пройтиnквадрантов в положительном направлении. На рис. 30 показаны примеры годографа Михайлова для устойчивых систем приn=2,n=4,n=6.

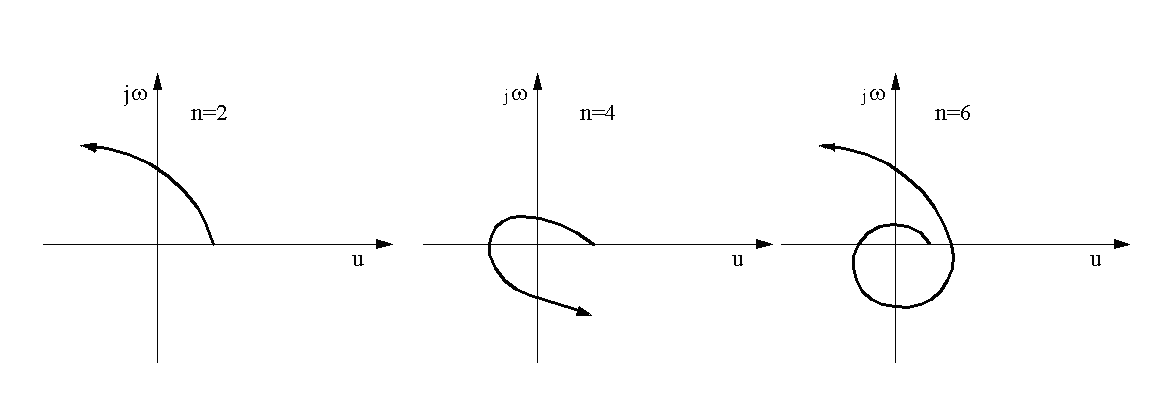
Рис. 30

Амплитудно-фазовый критерий (критерий Найквиста)

Допустим, имеется замкнутая динамическая система, уравнение которой составить трудно, поскольку свойства звеньев не поддаются простому математическому описанию. Вместе с тем, существует возможность построить макет системы или собрать ее из натурных элементов и исследовать свойства системы и звеньев экспериментально, частотным методом. При этом система размыкается. Найквист доказал, что по поведению разомкнутой системы можно судить об устойчивости замкнутой системы, построив для нее амплитудно-фазовую характеристику (подставив в выражение передаточной функции вместо символа р величину jω). По расположению АФХ на плоскости комплексного переменного можно судить об устойчивости замкнутой системы. Если уравнения нет, АФХ строится на основе опытных данных. Условие устойчивости по виду АФХ сформулировано Найквистом следующим образом.

Если разомкнутая система устойчива, то для устойчивой замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы не охватывала точку с координатами –1,j0.

Рис. 31 Иллюстрация к критерию Найквиста

В качестве примера рассмотрим применение критерия Найквиста к анализу системы, включающей звенья, описываемые последовательным соединением апериодического звена и звена запаздывания. Передаточная функция такой цепочки:

W_k(p)exp(-pτ_k),

где W_k(p) – передаточная функция апериодического звена,τ_k– время запаздывания. Если система содержит некоторое количество таких звеньев, то ее передаточная функция:

W^/(p)=W₁(p)W₂(p)W₃(p)…exp[-p(₁+τ₂+τ₃…)]=W^//(p) exp(-p τ),

где τ–суммарное время разомкнутой системы.

Частотная передаточная функция:

W^/(jω)=W^//(jω)exp(-jωτ).

Комплексное число W^//(jω) может быть представлено в полярной форме как произведение модуля и экспоненты фазового угла ν, тогда частотная передаточная функция разомкнутой системы:

W^/(jω)=W^//(jω)expj[ν(ω)-ωτ].

Для оценки устойчивости системы с запаздыванием необходимо:

1. найти значение частоты, при котором модуль частотной передаточной функции W^//(jω) = 1;

2. подставив найденное значение в выражение для фазового угла, убедиться в том, что этот угол не достигает величины –π.