6. Виды регуляторов

Как было показано ранее, наиболее распространенная задача управления – поддержание заданных законов изменения во времени параметров объекта (регулирование). Устройство, осуществляющее управляющее воздействие, называется регулятором. Регуляторы включают в себя простые динамические звенья, комбинируя которые добиваются требуемых переходных характеристик системы управления при случайных воздействиях и изменении нагрузки. При этом входным параметром для регулятора является один или несколько показателей работы объекта:

• величина и знак отклонения управляемого параметра от заданного значения (рассогласование) Δφ = φ-φ₀

• производная (скорость рассогласования по времени) ,

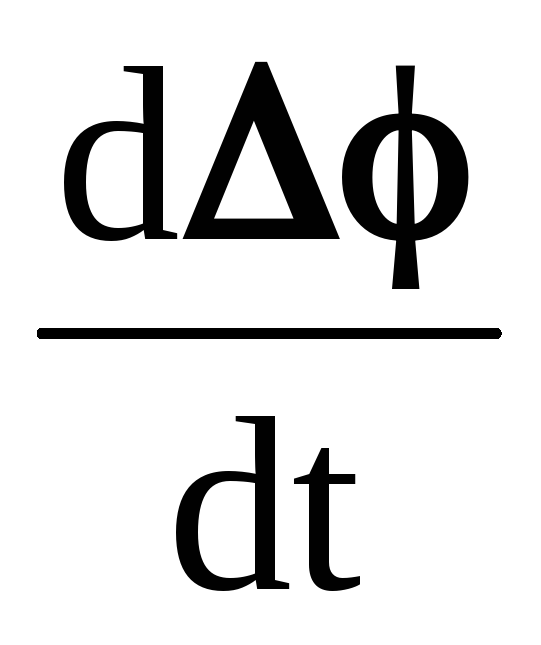• интеграл величины рассогласования во времени .

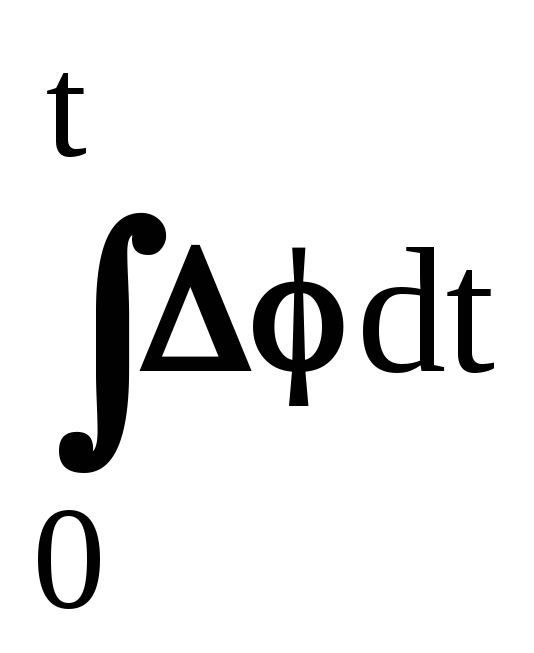В зависимости от того, как формируется управляющее воздействие, различают законы управления и соответствующие им регуляторы:

• релейные, реализующие нелинейный двухпозиционный закон управления

• пропорциональные (статические, или устройства с жесткой обратной связью)

• интегральные (астатические, устройства без обратной связи)

• пропорционально-интегральные, (изодромные, или устройства с исчезающей обратной связью)

• пропорционально-дифференциальные (статические устройства с предварением)

• пропорционально-интегрально-дифференциальные (изодромные устройства с предварением).

Применительно к установкам с ДВС релейный закон управления реализуется в системах регулирования давления и уровня, с помощью двухпозиционного реле включаются и отключаются насосы и компрессоры. Чтобы избежать слишком частых пусков и остановок механизмов устанавливается определенный интервал между значениями управляемого параметра, соответствующего включению и отключению реле (зона нечувствительности).

Остальные законы управления реализуются в основном в регуляторах скорости.

График регулирования по релейному закону представлен на рис. 23.

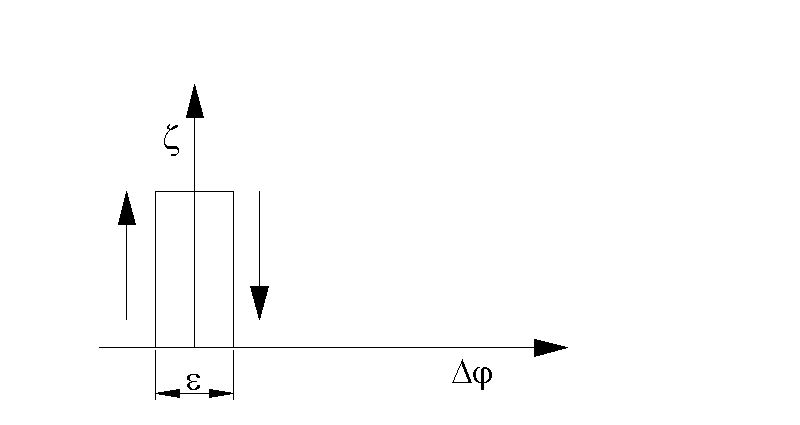
Рис.23

Пропорцинальные регуляторы вырабатывают управляющее воздействие в виде линейной зависимости от отклонения от отклонения регулируемого параметра:

ζ= -k_pΔφ,

где k_p– коэффициент усиления по регуляторному каналу.

Зависимость управляющего воздействия от отклонения регулируемого параметра показана на рис.24.

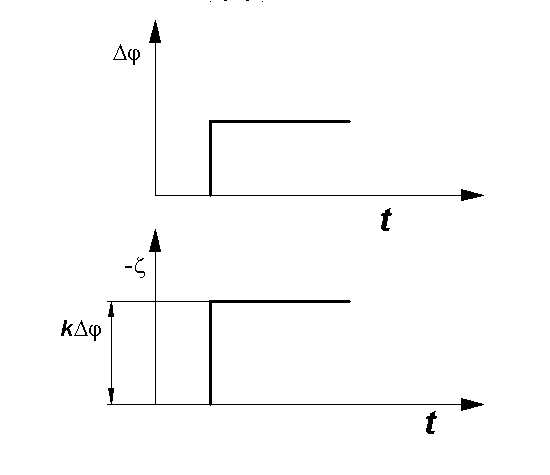
Рис.24

Так как в установившемся режиме определенной нагрузке должно соответствовать определенное положение регулирующего устройства, невозможно осуществлять регулирование во всем диапазоне нагрузок без определенной ошибки, называемой статизмом регулятора:

Интегральные регуляторы реализуют закон управляющего воздействия в виде формулы:

,

где Т_и– время интегрирования.

Интегральный регулятор может использоваться как предельный выключатель, предохраняющий систему от выхода за установленные допустимые пределы отклонения регулируемой величины в случае возникновения неисправности.

Всережимные регуляторы должны обеспечивать изменение регулируемой величины во всем диапазоне задаваемых значений независимо от нагрузки. В сумматор поступает сигнал по измерительному каналу от фактического значения параметра и по каналу задающего устройства. Чтобы улучшить характеристики переходного процесса при изменении режима или при случайных воздействиях, в регулирующие устройства вводят интегральное или дифференциальное звено или оба этих звена, работающих поочередно.

В пропорционально-интегральных регуляторах управляющее воздействие описывается уравнением:

,

где первое слагаемое определяет пропорциональную часть, а второе – интегральную.

В пропорционально-дифференциальных регуляторах управляющее воздействие описывается уравнением:

где Т_д– время дифференцирования.

Такие регуляторы позволяют временно увеличить величину управляющего воздействия и сократить время выхода на новый установившийся режим.

В пропорционально-дифференциальных-интегральных регуляторах управляющее воздействие описывается уравнением:

Такие регуляторы позволяют добиться наилучших показателей переходного процесса путем и добиться нулевого отклонения регулируемой величины от заданного значения во всем диапазоне нагрузок.

Все перечисленные виды регуляторов первоначально были реализованы в отечественной промышленности в виде приборов и агрегатов универсальной системы элементов промышленной пневмоавтоматики (УСЭППА). Недостатком этих приборов являлось наличие калиброванных отверстий и каналов малого диаметра, которые могли засоряться при некачественной подготовке рабочей среды (воздуха). В настоящее время применяются электронные регуляторы, в которых операции дифференцирования и интегрирования выполняются с помощью электронных схем и микропроцессоров.

Ранее существовали другие виды классификации регуляторов.

По способу энергетического воздействия измерительной части регулятора на его исполнительную часть регуляторы делятся на два класса: регуляторы прямого и непрямого действия. На рис.25 а показана блок-схема системы управления с регулятором прямого действия, на рис 25 б – с регулятором непрямого действия.

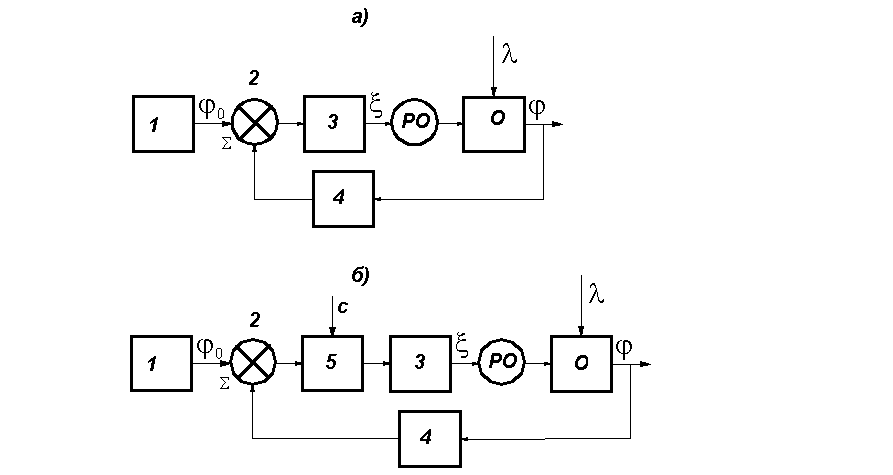
Рис. 25

1- элемент задания, 2 – элемент сравнения, 3 – исполнительный механизм, 4 – чувствительный элемент, 5 – усилитель, РО – регулирующий орган, О - объект

Регулятор прямого действия состоит из измерительного устройства, (включающего чувствительный элемент 4, элемент задания 1 и элемент сравнения 2), и исполнительного механизма 4, осуществляющего перестановку регулирующего органа в нужном направлении. Исполнительный механизм должен обладать вполне определенным выходным (или, как принято называть, перестановочным) усилием для перемещения РО. В регуляторе прямого действия необходимое перестановочное усилие вырабатывается чувствительным элементом.

В случае, когда нельзя спроектировать компактный чувствительный элемент, развивающий необходимое усилие, в конструкцию регулятора вводится усилитель 5, использующий дополнительную внешнюю энергию (с) для усиления мощности измерителя. Такой регулятор называется регулятором непрямого действия.

По способу обеспечения задачи регулирования регуляторы делились на следующие классы:

• астатические регуляторы

• статические регуляторы

• программные регуляторы

• двухпозиционные регуляторы.

На примерах простейших регуляторов давления можно понять отличие в конструкции статических и астатических регуляторов. На рис. 26 показан астатический регулятор давления.

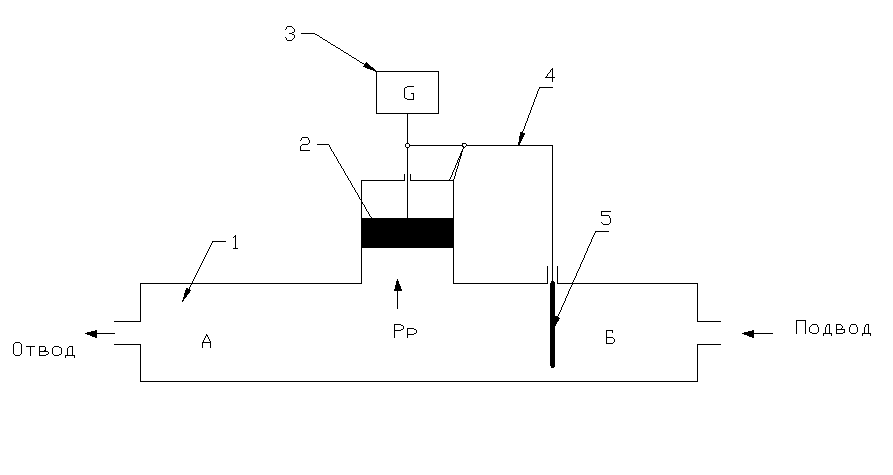
Рис. 26 Астатический регулятор давления

1 – регулируемый объект, 2 – поршень (чувствительный элемент), 3 – груз (элемент задания и элемент сравнения), 4 – передаточный рычаг (исполнительный механизм), 5 – шибер (регулирующий орган )

В потоке газа имеется регулирующее устройство 5 с изменяемым сопротивлением, благодаря которому при переменном давлении на подводе можно поддерживать постоянное давление в полости А. В равновесном режиме имеется баланс между подводом и отводом газа, давление в рабочей полости А соответствует расчетному значению Р_ри уравновешивается грузомG. При изменении нагрузки (отвода) баланс нарушается и в зависимости от характера наступившего изменения уменьшается или увеличивается давление в полости А. Поршень (чувствительный элемент начинает перемещаться, открывая или закрывая шибер. Когда вновь будет достигнуто исходное значение Р_р, может наступить равновесие при новой нагрузке. Однако получить новое устойчивое равновесие без постоянных колебаний далеко не всегда удается. Это основной недостаток астатических регуляторов.

В статическом регуляторе (рис. 27) элементом задания является верхняя опора пружины 4, элементом сравнения является пружина 3. Величина усилия, действующая на поршень со стороны пружины, меняется в зависимости от положения поршня по высоте. Из-за этого возникает не одно, как в предыдущем случае, а множество равновесных состояний по давлению. Так, если давление Р начало возрастать, поршень, поднимаясь и сжимая пружину, может занять новое положение, при котором возросшему давлению будет отвечать возросшее усилие пружины. Таким образом, статический регулятор с заведомо предусмотренной статической ошибкой. Значение поддерживаемого параметра однозначно связано с величиной нагрузки.

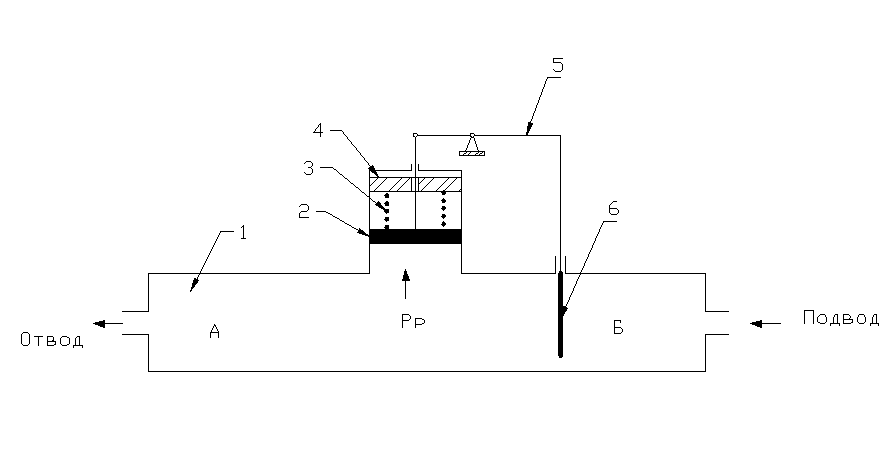
Рис. 27 Статический регулятор давления

1 – регулируемый объект, 2 – поршень (чувствительный элемент), 3 – пружина (элемент сравнения), 4 – верхняя опора пружины (элемент сравнения), 5 - передаточный рычаг (исполнительный механизм), 6 – шибер (регулирующий орган )

В программных регуляторах предусматривается дополнительный конструктивный элемент, изменяющий координату задания, а, следовательно, и регулируемую величину, по определенной функциональной зависимости от нагрузки, от времени или от других величин.

В двухпозиционных регуляторах реализуется релейный закон управления. Регуляторы этого типа работают по принципу включено – выключено.