4. Определение φ Пример расчета φ нормативным методом

Расчет φпо нормативному методу производится с помощью следующей формулы:

φ=Сβ

где С – коэффициент пропорциональности, определяемый по номогорамме 6 из [1].

При этом приходится учитывать следующие условия:

1) расчет справедлив для p>10 атм;

2) расчет справедлив для d_тр>30 мм, еслиd_тр<30 мм, то необходимо делать поправку.

Расчетная скорость смеси:

Вычисления производятся для среды пар–вода при температуре насыщения.

При p=6,9 Мпа и= 6,71 получаем:

С=0,761

Тогда φрассчитаем следующим образом:

Расчет φ с помощью коэффициента скольжения

Для определения истинного объемного паросодержания двухфазной смеси через коэффициент скольжения, используем следующую модель:

где коэффициент скольжения определяется по формуле Zivi:

Получим значение φ

Сводная таблица расчётов φ тремя методами

Таблица 4.1

z	iz	x	ϕнорм	c	ϕ через S	S
0	1231,5	-0,021	0,000	0,000	-0,531	1,197
0,1	1259,6	-0,0019	0,000	0,000	-0,034	1,197
0,2	1287,8	0,017	0,198	0,761	0,227	1,197
0,3	1316,0	0,035	0,328	0,762	0,387	1,197
0,4	1344,1	0,054	0,413	0,763	0,496	1,197
0,5	1372,3	0,073	0,472	0,764	0,574	1,197
0,6	1400,5	0,091	0,516	0,765	0,634	1,197
0,7	1428,6	0,110	0,550	0,766	0,680	1,197
0,8	1456,8	0,129	0,577	0,767	0,718	1,197
0,9	1485,0	0,147	0,600	0,768	0,748	1,197
1	1513,1	0,166	0,618	0,769	0,774	1,197
1,5	1653,9	0,259	0,676	0,770	0,858	1,197
2	1794,8	0,352	0,740	0,770	0,904	1,197
2,5	1935,6	0,446	0,810	0,770	0,933	1,197
3	2076,4	0,539	0,850	0,770	0,953	1,197
3,5	2217,2	0,632	0,900	0,770	0,967	1,197
4	2358,1	0,725	0,930	0,770	0,978	1,197
4,5	2498,9	0,819	0,960	0,770	0,987	1,197
5	2639,7	0,912	0,980	0,770	0,994	1,197
5,5	2780,5	1,005		0,770	1,000	1,197
6	2921,4	1,098		0,770	1,005	1,197
6,5	3062,2	1,192			1,009	1,197

Графики зависимости φ и β отx

Рис.3 Графики зависимости φ и β от x

5. Расчет коэффициента теплоотдачи и температуры стенки для всей трубы

Способ расчёта будет меняться с изменением массового паросодержания.

, (29)

где = 0,285 ·– кинематическая вязкость воды, значение которой мы берём в [3].

Т.к. Re> 2000, то воспользуемся формулой Михеева для расчёта Nu:

Nu = 0,023 · ·= 0,023 ·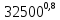·= 726, (30)

где = 1,678 согласно [3]. На темпр насыщ

Запишем общую формулу для Nu и выведем из неё .

Nu = (31)

Откуда

= == 31000, (32)

Здесь = 0,677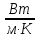– коэффициент теплопроводности из [1]. На темпр насыщ

Вычислим коэффициент теплоотдачи при кипении в большом объеме

= 4,32 · (+ 1,28 ··) ·= 4,32 · (+ 1,28 ··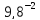)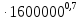= 248000(33)

= 8> 3,

Следовательно,

Определяем значение расходного массового паросодержания , при котором прекратится орошение стенки. Для этого используем таблицу [4].

Для заданных условий

1. При 0 < x <

   (34)

= += 310 += 316 °C

Из Рис.8.22 (а) [2] определим, что теплоотдача окисленных труб = 21200, а следовательно, согласно Рис.8.22 (б), поправочный множитель К = 5.

2. <x ≤ 1

Подставим значения для х=0,88.

Определим значение числа Рейнольдса для перегретого пара

Найдем коэффициент

Рассчитаем число Нуссельта

где - число Прандтля для перегретого пара.

Определим коэффициент теплоотдачи на участке ухудшенного теплообмена

где - коэффициент теплопроводности перегретого пара, Вт/(м·К).

Найдем температуру стенки

(39)

3. x> 1

Возьмем х=1,5.

Рассчитаем энтальпию перегретого пара

Следовательно температура перегретого пара будет равна =778,9⁰С.

Определим значение числа Рейнольдса для перегретого пара

=,(42)

Рассчитаем число Нуссельта для перегретого пара

Найдем коэффициент теплоотдачи для перегретого пара

Теперь определим температуру стенки

Все данные для остальных точек трубы занесены в таблицу 5.1. Построен график температуры стенки рис 3.1.

Как видно из графика в зоне ухудшенного теплообмена температура стенки незначительно увеличивается.Такой режим не опасен для труб.

Таблица 5.1

x	α	Tw
0,0003	248000	316
0,0069	248000	316
0,0136	248000	316
0,0202	248000	316
0,85	354	694
0,88	358	690
0,94	361	687
1	331	721
1,5	194	1465

Рис.4

Выводы

Руководствуясь полученными результатами, можно сделать вывод о том, что уровень теплоотдачи с поверхности, покрытой продуктами коррозии, снижается, поэтому при одной и той же плотности теплового потока перегрев жидкости, кипящей на поверхности окисленной трубы, будет меньше, чем при кипении на поверхности чистой трубы.

Был рассчитан коэффициент теплоотдачи для разных участков кипения воды, в том числе и для области ухудшенного теплообмена. Выявлена зависимость Т(x). Анализируя ее, можно сделать вывод, что в области с паросодержанием, значительно превышающем граничное, наблюдается существенное превышение температуры стенки над температурой среды.