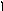7

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖЕНЕРНО – СТРОИТЕЛЬНЫЙ

КАФЕДРА ФИЗИКИ И ОБЩЕЙ ЭЛЕКТРОТЕХНИКИ

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 5

по дисциплине

ЭЛЕКТРОТЕХНИКА

Выполнил ст. гр. УИТ-23

Герт А.А.

Принял преподаватель

Олькова В.Б.__________

«___»___________2002 г.

2002

Задание 1

Рассчитать и построить зависимости u_cb, u_ac, u_ab, , i₃, i₂ от t.

Данные

m, Bc	Im, A	XL, Ом	R, Ом	
10–2	0.5	200	200	2000

Схема:

i₃

a

c

i

i₂

b

Где i=0.5sin2000t

Вебер-Амперная характеристика:

Анализ:

L₁₃= т.е. разрыв

L₁₂= L₃₄= т.е. закоротка

Найдем t₁:

t_1­­-время за которое дросель перемагничивается от -10^-2 до 10^-2 Вс.

Начальные условия: t=0, = -10^-2 Вс

Составим схему замещения:

i₃=0 А

i₂=i

u_L= i₂R=2000.5sin2000t=100sin2000t B

Во всех расчетах задачи u_ac=0 т.к. сопротивление на данном участке отсутствует, поэтому далее нахождение u_aс производить не будем.

По 2 з. Кирхгофа:

u_L= u_сb

u_L= u_ab

Найдем t₁:

t_1­­-время за которое дросель перемагничивается от -10^-2 до 10^-2 Вс.

Начальные условия: t=0, = -10^-2 Вс . Конечные условия t=t₁, = 10^-2 Вс

т.к. u_L= , то =>

подставляя начальные условия имеем:

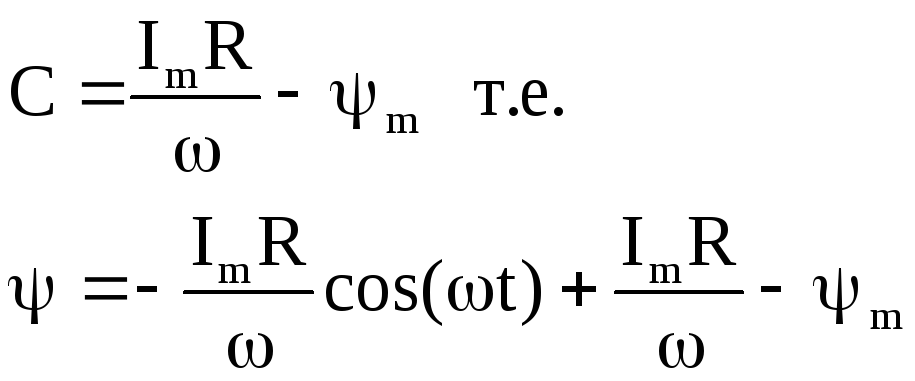
подставляя конечные условия имеем:

t₁=

Рассмотрим режим закоротки: (от t₁ до )

i₃

i

a

c

i₂

u_L

u_cb

u_ab

b

i₃=i A

i₂=0 A, т.к. ток течет по пути наименьшего сопротивления

u_cb = i₂R=0 B

u_ab = u_cb = 0 B

На основе анализа можем построить требуемые зависимости:

Задание 2

Провести расчет периодических процессов в нелинейных электрических цепях с помощью ВАХ по первым гармоникам токов и напряжений. Построить их векторные диаграммы, считая что источник питания н входе схемы имеет неизменную частоту.

Схема:

R=100 Ом

X_L=100 Ом

Задаваясь различными значениями тока I₁ построить для всей схемы несколько векторных диаграмм по первой гармонике и найти зависимость U_ab(I₁).

По законам Кирхгофа, имеем:

U­_ab=U₁+U₃ U­_ab=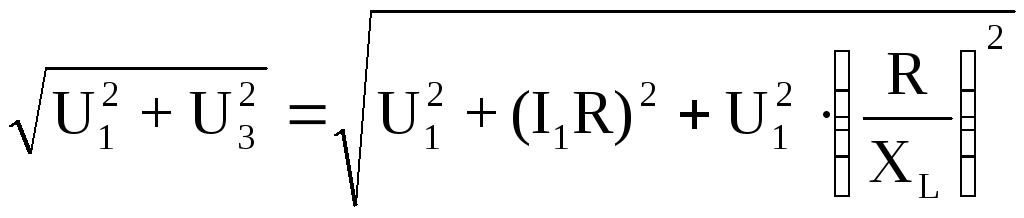

I₃= I₁+ I₂ I₃= I₁+

U₁-I₂ jX_L=0 I₂=

Где U₃=I₃R U₃=I₁R+ R

U₂=I₂ jX_L U₂=I₂ jX_L

Зададим значения U₁(I­₁) по графику и найдем вышеописанные величины:

U1(I1), B	U­ab, В	U3, B	U2, B	I3, A	I2, A
U1(0,4)=10	42.43	40+j10	10	0.4+j0.1	–j0.1
U1(0,8)=20	82.46	80+j20	20	0.8+j0.2	–j0.2
U1(1)=40	107.70	100+j40	40	1+j0.4	–j0.4
U1(1,2)=80	144.22	120+j80	80	1.2+j0.8	–j0.8
U1(1,4)=120	184.39	140+j120	120	1.4+j1.2	–j1.2
U1(1,6)=200	256.12	160+j200	200	1.6+j2	–j2

Построим зависимость Uab(I1):	Векторная диаграмма U3 0 40 80 120 160 200 +j U, B 200 160 120 80 40
Совмещенная векторная диаграмма U2 и I2 200 160 120 80 40 -j –2 –1.6 –1.2 –0.8 –0.4 0	В U, B 2 16 1.2 0.8 0.4 0 0.4 0.8 1.2 1.6 2 +j екторная диаграмма I3