разное к тоэ / Работа67abc

14

Вариант № 67

С хема:

Исходные данные:

R₁ = 260 Ом; R₂ = 80 Ом; R₃ = 120 Ом; R₄ = 160 Ом; R₅ = 220 Ом; R₆ = 90 Ом;

E₁ = 24 В; E₂ = 34 В; I_k1 = 0 А; I_k2 = 0,2 А.

1. Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.

В данной схеме количество узлов n = 5, количество ветвей m = 10, количество ветвей с источником тока m_J = 2.

Для данной схемы можно составить (n – 1) = 4 уравнений по 1 закону Кирхгофа:

-I₃ + I₅ + I₆ = 0

-I₁ + I₂ – I₅ = 0

-I₂ + I₃ – I₄ = 0

I₂ – I₂’ + I_k2 = 0

и (m – m_J) – (n – 1) = 3 уравнения по 2 закону Кирхгофа:

-I₂R2 – I₃R₃ – I₅R₅ = E’₂

I₃R₃ + I₄R₄ + I₆R₆ = 0

-I₁R₁ + I₅R₅ – I₆R₆ = E₁

2. Определить токи во всех ветвях схемы методом контурных токов.

П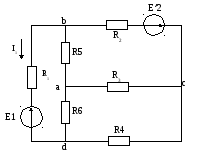 редварительно заменим источники тока источниками ЭДС. Получим схему:

E₂’ = E₂ + I_k2*R₂

Выберем контурные токи, как показано на схеме.

Запишем выражения реальных токов через контурные.

I₁ = -I₃₃

I₂ = -I₁₁

I₃ = -I₁₁ + I₂₂

I₄ = I₂₂

I₅ = -I₁₁ + I₃₃

I₆ = I₂₂ + I₃₃

Запишем уравнения по 2 закону Кирхгофа через контурные токи.

I₁₁(R₂ + R₃ + R₅) – I₂₂R₃ – I₃₃R₅ = E’₂

I₂₂(R₄ + R₃ + R₆) – I₁₁R₃ – I₃₃R₆ = 0

I₃₃(R₅ + R₆ + R₁) – I₁₁R₅ – I₂₂R₆ = E₁

Решим полученную систему матричным методом относительно контурных токов.

3. Определить токи во всех ветвях схемы методом узловых потенциалов.

В данной схеме заземлим узел a (_a = 0).

Запишем уравнения по 2 закону Кирхгофа через потенциалы узлов и проводимости.

_b(g₅ + g₂ + g₁) - _cg₂ - _dg₁ = E₁g₁ – E₂’g₂

_c(g₂ + g₃ + g₄) - _bg₂ - _dg₄ = E₂’g₂

_d(g₄ + g₆ + g₁) - _bg₁ - _cg₄ = -E₁g₁

Решим полученную систему матричным методом относительно потенциалов узлов.

Рассчитаем токи в ветвях, используя закон Ома для активного участка цепи.

I₁ = (-E₁ + _b - _d)g₁

I₂ = (-E’₂ + _c - _b)g₂

I₃ = (_a - _c)g₃

I₄ = (_c - _d)g₄

I₅ = (_b - _a)g₅

I₆ = (_d - _a)g₆

4. Результаты расчета токов, проведенного 2 методами, свести в таблицу и сравнить между собой.

	I1, A	I2, A	I3, A	I4, A	I5, A	I6, A
МКТ	-0,147	-0,227	-0,118	0,11	-0,08	-0,038
МУП	-0,147	-0,227	-0,118	0,11	-0,08	-0,038

Как видно из таблицы, оба метода расчета токов дали одинаковые результаты.

5. Составить баланс мощностей в исходной схеме (схеме с источником тока), вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений).

Найдем суммарную мощность источников

P_ист. = E₁I₁ + E₂’I₂.

P_ист. = 24*0,147 + (34+0,2*80)*0,227 = 14,906.

Найдем суммарную мощность приемников

P_пр. = I₁²R₁ + I₂²R₂ + I₃²R₃ + I₄²R₄ + I₅²R₅ + I₆²R₆.

P_пр. = 0,147²*260 + 0,227²*80 + 0,118²*120 + 0,11²*160 + 0,08²*220 + + 0,038²*90 = 14,906.

P_ист. = P_пр.

6. Определить ток I₁, в заданной по условию схеме с источником тока, используя теорему об активном двухполюснике и эквивалентном генераторе.

В ыделим ветвь, по которой протекает ток I₁, и рассчитаем его, используя теорему об активном двухполюснике и эквивалентном генераторе. Оставшуюся часть схемы будем считать активным двухполюсником:

Вычислим параметры эквивалентного генератора.

Найдем потенциалы узлов b и d методом узловых потенциалов.

Составим систему уравнений (b = 0):

_b(g₅ + g₂) - _cg₂ = -E₂’g₂

_c(g₃ + g₂ + g₄) - _bg₂ - _dg₁ = E₂’g₂

_d(g₄ + g₆) - _cg₄ = 0

Решим систему матричным методом.

Н айдем внутреннее сопротивление генератора

7. Начертить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.

_b = 0

_m = _b + I₂R₂ = -18.16В

_c = _m + E’₂ = 31.84В

_d = _c - I₄R₄ = 14.24В

_n = _d + E₁ = 38.22В

_b = _n + I₁R₁ = 0 В

П остроим потенциальную диаграмму.

8. В заданной схеме закоротить все источники ЭДС, разомкнуть сопротивления, шунтирующие источник тока, заземлить один узел схемы и один из узлов принять за сток.

Начертить сигнальный граф, используя уравнения, составленные для полученной схемы по методу узловых потенциалов. Требуется по формуле Мезона определить передачу от истока (источник тока) к стоку.

_b(g₁ + g₂ + g₅) - _cg₂ - _dg₁ = E₁g₁- E₂’g₂

_c(g₂ + g₃ + g₄) - _bg₂ - _dg₄ = E₂’g₂

_d(g₁ + g₄ + g₆) - _bg₁ - _cg₄ = -E₁g₁

Запишем их в виде:

_b = _ca + _db + E₁c + E₂’d

(c = (be + (df + E2’k

(d = (bm + (cn + E1p

где

a = g2/(g2 + g5 + g1) e = g2/(g2 + g3 + g4) m = g1/(g1 + g4 + g6)

b = g1/(g2 + g5 + g1) f = g4/(g2 + g3 + g4) n = g4/(g1 + g4 + g6)

c = g1/(g2 + g5 + g1) k = g2/(g2 + g3 + g4) p = -g1/(g1 + g4 + g6)

d = -g2/(g2 + g5 + g1)

С оставим по данным уравнениям сигнальный граф:

Воспользуемся методом наложения, найдем (b как сумму (b(1) и (b(2)

П рямые пути: c1,pb1,pfa1.

Контура: al,fn,bm,ben,abf.

В оспользуемся формулой Мезона:

Прямые пути: nba1, ne1.

Контура: al,fn,bm,ben,abf.

Воспользуемся формулой Мезона:

ﾵ ﾧ

(b =	(c1(1 - fn) + pb1 + pfd1)E’2 +(d1(1 - fn)+ka1+knb1)E1
	1 – al – fn – bm – ben – abf